正多面体的一个奇妙定值
广东省广州市赤坭圩小学(510830) 李思根
广东省广州市新华培新学校(510800) 洪鹏花
文[1-2]获得的结论是: 设球面O为正多面体的同心球面,P为球面O上任意一点,则P到正多面体各顶点的距离平方之和为定值;文[3]获得的结论是: 若正多面体的面数为F,内切球半径为r内,同心球的半径为R,则球面上任一点P到正多面体各面的距离的平方和为定值本文将给出正多面体的如下性质:
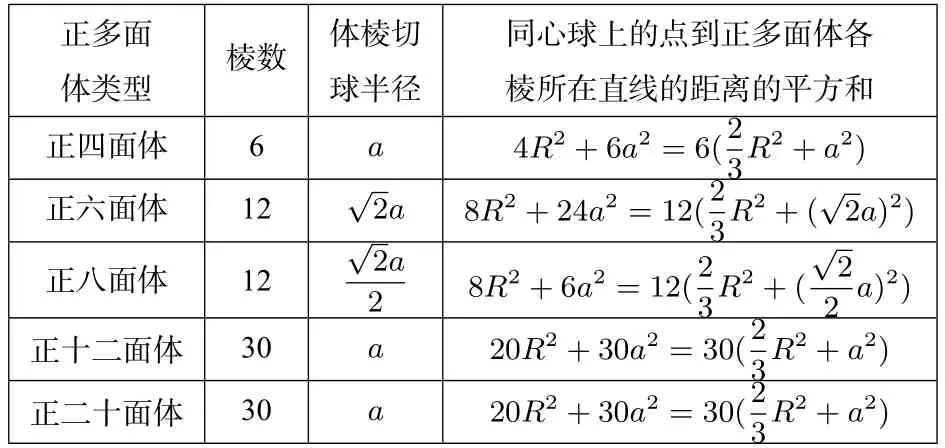
定理若正多面体的棱数为E,棱切球半径为r棱,同心球的半径为R,则球面上任一点P到正多面体各棱的距离的平方和为定值
注记与正多面体所有棱都相切的球称为正多面体的棱切球.显然正多面体的棱切球半径是正多面体的中心到棱中点的距离.
证明在文[4]第126-127 页中, 在空间直角坐标系下,点M0(x0,y0,z0)到直线l:的距离的平方

(1) 正四面体

设正四面体的同心球半径为R, 球面上的任意一点P0(x0,y0,z0) 到六条棱AC、BD、AB、CD、BC、AD所在直线的距离分别记为d1,d2,d3,d4,d5,d6, 显然

(2) 正六面体
设正六面体的棱长为2a, 三组对面中心点连线相交于一点, 如图建立空间直角坐标系, 显然点O为正六面体的中心, 则顶点坐标为A(a,a,a),B(−a,a,a),C(−a,−a,a),D(a,−a,a),A′(a,a,−a),B′(−a,a,−a),C′(−a,−a,−a),D′(a,−a,−a).十二条棱所在直线的方程为
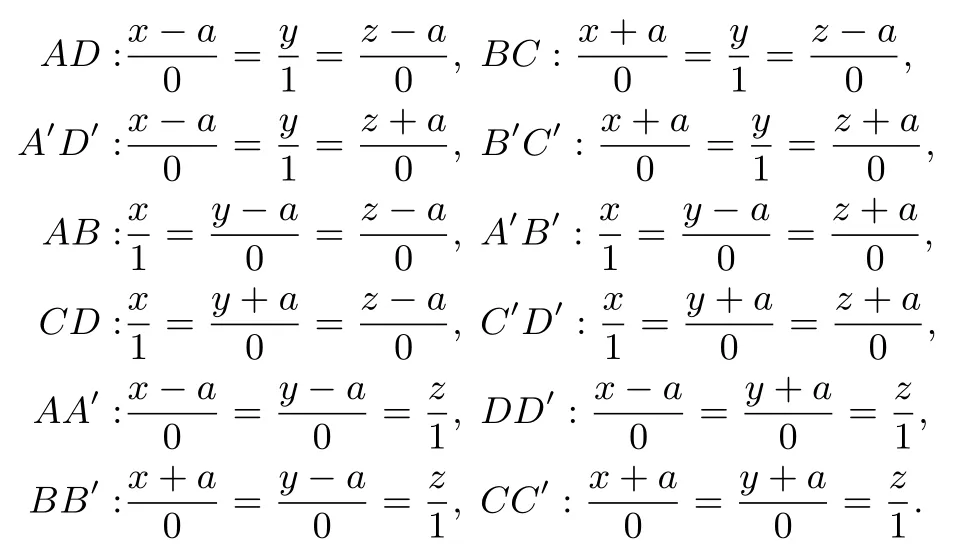
设正六面体的同心球半径为R, 球面上的任意一点P0(x0,y0,z0),到十二条棱AD、BC、A′D′、B′C′、AB、A′B′、CD、C′D′、AA′、DD′、CC′、BB′所在直线的距离分别记为d1,d2,d3,d4,d5,d6,d7,d8,d9,d10,d11,d12,显然


(3) 正八面体


设正八面体的同心球半径为R, 球面上的任意一点P0(x0,y0,z0),到十二条棱EA、EB、EC、ED、E′A、E′B、E′C、E′D、AB、BC、CD、DA所在直线的距离分别记为d1,d2,d3,d4,d5,d6,d7,d8,d9,d10,d11,d12,显然


(4) 正十二面体


则六条棱所在直线的方程为
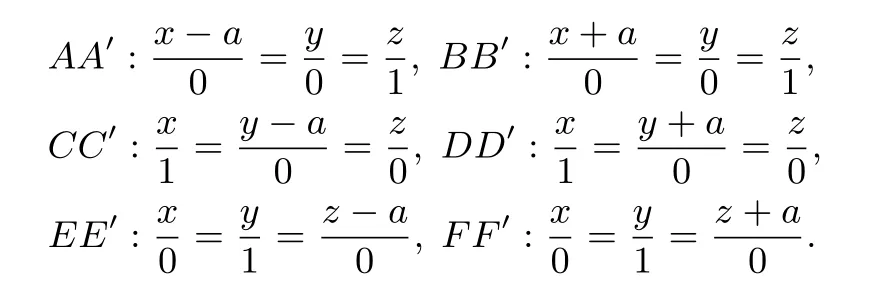
点P、Q分别为正五边形AGEE′H、B′MF′FN的中心,显然直线PQ过正十二面体的中心O,所以正十二面体的其他棱可以通过棱AA′、BB′、CC′、DD′、EE′、FF′绕直线PQ旋转得到.如果正十二面体的同心球面上的任意一点到棱AA′、BB′、CC′、DD′、EE′、FF′的距离平方和是定值Z,那么正十二面体的同心球面上的任意一点到所有棱的距离平方和是定值5Z.
设正十二面体的同心球半径为R, 球面上的任意一点P0(x0,y0,z0) 到六条棱AA′、BB′、CC′、DD′、EE′、FF′所在直线的距离分别记为d1,d2,d3,d4,d5,d6, 显然

(5) 正二十面体

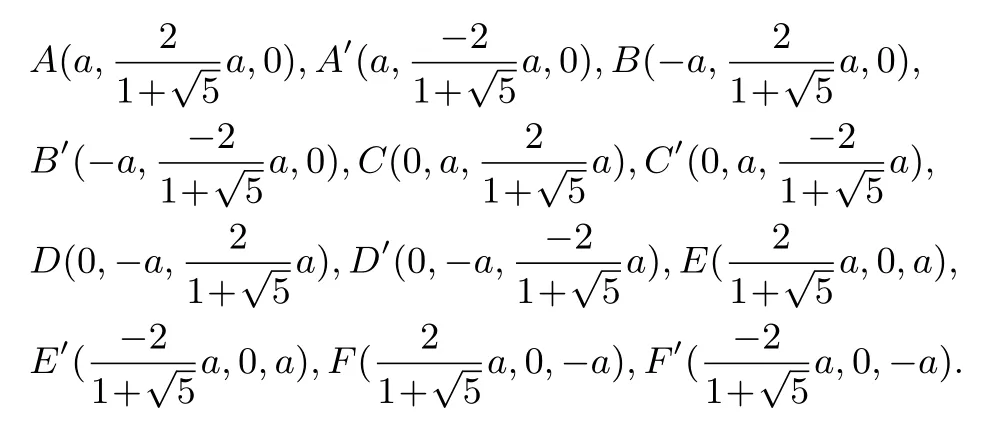
则六条棱所在直线的方程为

显然直线EF′过正二十面体的中心O,所以正二十面体的其他棱可以通过棱AA′、BB′、CC′、DD′、EE′、FF′绕直线EF′旋转得到.如果正二十面体的同心球面上的任意一点到棱AA′、BB′、CC′、DD′、EE′、FF′的距离平方和是定值Z,那么正二十面体的同心球面上的任意一点到所有棱的距离平方和是定值5Z.
设正二十面体的同心球半径为R, 球面上的任意一点P0(x0,y0,z0) 到六条棱AA′、BB′、CC′、DD′、EE′、FF′所在直线的距离分别记为d1,d2,d3,d4,d5,d6, 显然
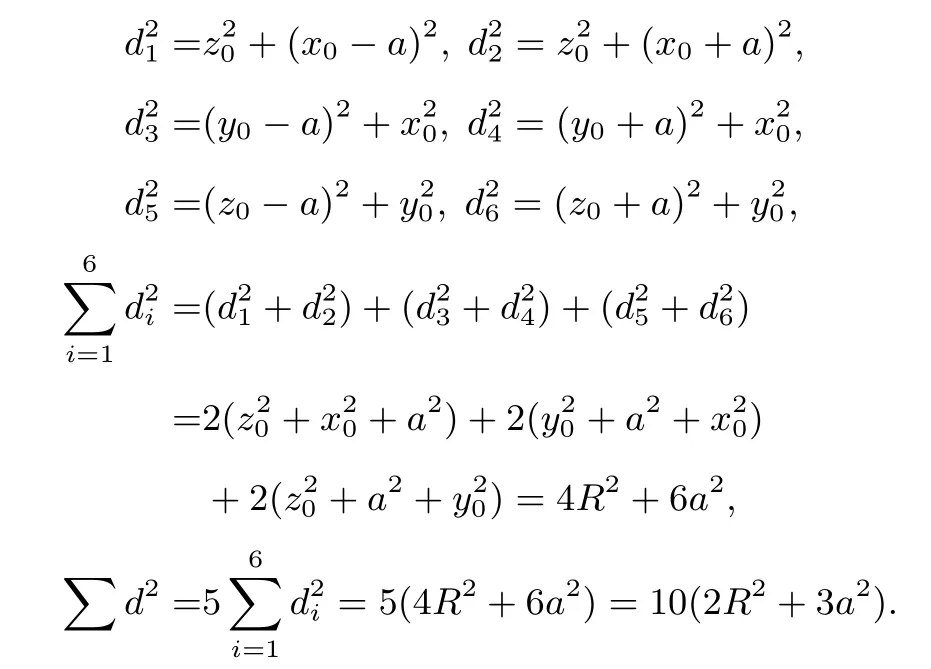
将上述结论整理成表格如下:
正多面______________________体类型棱数体棱切球半径_____同心球上的点到正多面体各棱所在直线的距离的平方和____正四面体6 a 4R2+6a2 =6(2 3R2+a2)正六面体12√2a 8R2+24a2 =12(2 3R2+(__√2a)2)正八面体12√2a 2 8R2+6a2 =12(2 3R2+(√2 2 a)2)_正十二面体30 a 20R2+30a2 =30(2 3R2+a2)___正二十面体30 a 20R2+30a2 =30(2 3R2+a2)___
因此,若正多面体的棱数为E,棱切球半径为r棱,同心球的半径为R,则球面上任一点P到正多面体各棱的距离的平方和为定值

