挖掘基本模型 探求问题本质*
广东省佛山市罗定邦中学(528300) 龙 宇
在高考题中,关于立体几何的考察一般都是“两小”(选择或填空)“一大”(解答题).在历年的高考题中,出现了一大批经典的好题.笔者为了给高三复习准备资料,特意梳理了一下,发现2009年全国卷理科第8 题是一道难得的好题,笔者从模型化的角度对该问题进行了深度的分析,现将研究的过程整理如下,以飨读者.
一、引例
题目(2009年高考全国卷理科第8 题) 如图1, 正方体ABCD −A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=则下列结论中错误的是( )
A.AC⊥BE
B.EF//平面ABCD
C.三棱锥A −BEF的体积为定值
D.异面直线AE,BF所成的角为定值
分析本题是在正方体的基础上,考察线面的位置关系,三棱锥的体积问题以及异面直线的夹角问题.该图形是学生所熟知的图形,考察的知识点也是平时教学的重点内容,但是又稳中有变,四个选项均是在E,F运动的状态下进行判断的结论.该题可求解的方法很多,即可使用传统几何法,也可使用向量法进行求解.
解析点E在运动的过程中,直线BE形成的“轨迹”⊂平面BDD1B1, 显然AC⊥平面BDD1B1, 故选项A 是真命题.
点E,F在运动的过程中,EF始终⊂B1D1,在立方体中,B1D1//平面ABCD显然成立,故选项B 是真命题.
根据三棱锥的体积公式VA−BEF=· S∆BEF ·dA−BEF, 其中面BEF= 平面BDD1B1, 故点A到平面BEF的距离等于点A到平面BDD1B1的距离, 即有dA−BEF=考虑∆BEF, 其面积为:S∆BEF=·dB−EF,显然可知BB1⊥EF,故dB−EF=BB1=1,则有S∆BEF=带入体积公式即有V=为定值,故选项C 是真命题.______

图2
关于选项D, 本文仅介绍传统几何法, 关于异面直线的夹角, 一般通过平行关系, 平移一条直线与另一条直线相交, 将原问题转化为相交直线的夹角问题.具体操作如下: 如图2, 连接BD与AC交于点O, 连接OE,显然可得EFBO为平行四边形,故有BF//OE.异面直线AE,BF所成角的大小为: ∠AEO,考虑∆AEO,AO⊥OE,tan ∠AEO=其中OE为变量, 故异面直线AE,BF所成的角不是定值,选项D 错误.
二、总结模型,探究本质
本题以正方体为背景,而其中的很多边在解题过程中并没有涉及,为了探求其本质特征,现去掉其多余的边,仅保留题目涉及到的图形,具体如图3.原题干改编如下:
已知空间中的两条异面直线AB与B1D1的夹角为两者之间的距离为1,AB= 1,B1D1=√E,F为B1D1上的动点, 且EF=(上述信息丢失了BB1⊥B1D1).在该背景下,上述四个选项(除选项A 外)的判断方式不变.再观察可知,B1D1主要提供位置信息,其长度信息在判断的过程中意义不大.

图3
为此, 我们提出更一般的模型: 如图4, 已知空间中的两条异面直线l1与l2的夹角为θ, 两者之间的距离为t,A,B是l1上的动点,E,F是l2上的动点, 且AB=m,EF=n.接下来,我们仅考虑三棱锥A −BEF的体积问题,其他三个选项均与位置信息相关,本文不在探讨.
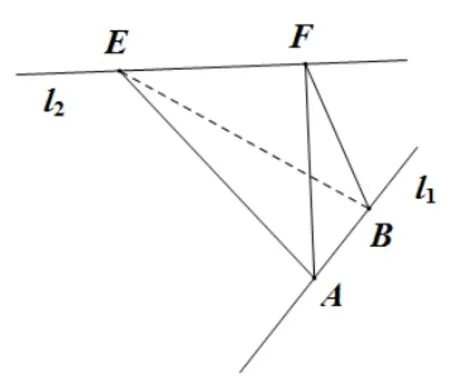
图4
分析本题涉及到的动点较多,先固定点A,B,由点B为一个定点, 由点B及直线l2可确定唯一一个平面, 记为平面α, 由点A也为定点, 则可得点A到平面α的距离为定值, 即可得三棱锥A −BEF的高为定值, 在平面α内,点B到直线l2的距离也为定值, 且EF也为定值, 即可得∆BEF的面积为定值,根据体积公式:V=可知三棱锥A −BEF的体积为定值.接下来固定点E,F,让点A,B作为动点,同理可知三棱锥A −BEF的体积为定值.那这个定值具体是多少呢?
为了便于计算, 移动点B,F使得BF为直线l1,l2的公垂线,如图5,过点B做l2的平行线l3,记由点B及直线l2所构成的平面为α,过点A作l3的垂线,垂足为D,根据三垂线定理易得AD⊥平面α.
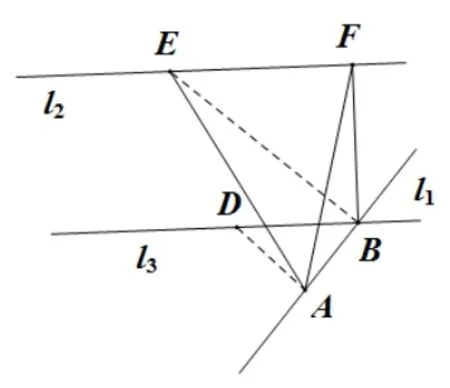
图5
在三棱锥A −BEF中,dA−BEF=AD=nsinθ,S∆BEF=带入体积公式即可得:V=
根据上面总结的模型,我们可以编制出如下的变式供读者练习.
变式1如图6-1, 在长方体ABCD −A1B1C1D1中,AD=2,AB=BB1=1,线段B1D1上有两个动点E,F,且EF= 1,求三棱锥A −BEF的体积.

图6 -1
变式2如图6-2, 在长方体ABCD −A1B1C1D1中,AD=2,AB=BB1= 1, 线段B1D1上有两个动点E,F, 且EF= 1,线段AB上有两个动点P,Q, 且PQ=求三棱锥P −QEF的体积.

图6 -2
变式3如图6-3,平行六面体ABCD −A1B1C1D1的体积为2,底面ABCD为矩形,AD= 2,AB=BB1= 1, 线段B1D1上有两个动点E,F, 且EF= 1,线段AB上有两个动点P,Q, 且PQ=求三棱锥A −BEF的体积.

图6 -3
三、探究该模型下的面积问题
在原问题背景下, 三棱锥A −BEF的体积为定值, 那么它的表面积是否为定值呢? 根据上面的分析, 可以得到∆AEF, ∆BEF的面积分别为定值.现考虑∆EAB以及∆FAB,其中A,B为定值,只需考虑点E,F到直线AB的距离.
如图7, 过点E,F分作BD的垂线, 垂足为E1,F1, 过点E1,F1分别做AB的垂线,垂足为E2,F2,连接EE2,FF2.根据三垂线定理,EE2,FF2分别为点E,F到直线AB的距离.
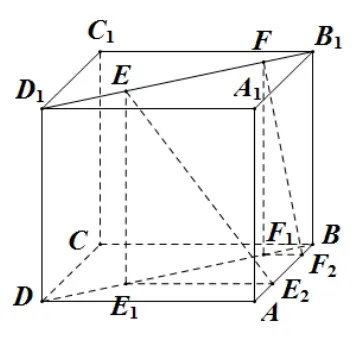
图7
设F1F2=x,考虑梯形E1E2F2F1,可得E1E2=x+根据勾股定理:EE2=原问题转化为求解函数f(x) =的最值问题.
显然可得f(x)为增函数,当x=0 时,f(x)取到最小值为+1, 结合题目的背景, 当x=时,f(x)取到最大值为则有三棱锥A −BEF的表面积的范围是
在一般模型下, 易知对应的三棱锥的表面积无最大值,我们仅考虑一般模型下, 表面积的最小值问题.即如图4,已知空间中的两条异面直线l1与l2的夹角为θ, 两者之间的距离为t,A,B是l1上的动点,E,F是l2上的动点, 且AB=m,EF=n.求三棱锥A −BEF的表面积的最小值.

图8
仿照上面的分析过程, 我们可以先固定点A,B, 仅考虑点E,F为动点的情况.求得最小值后, 再固定E,F, 让点A,B为动点.具体操作如下: 如图8,过点B做l2的平行线l3,记由直线l1与直线l3所构成的平面为β,过点E,F分作平面β的垂线,垂足为E1,F1,过点E1,F1分别做AB的垂线,垂足为E2,F2,连接EE2,FF2.根据三垂线定理,EE2,FF2分别为点E,F到直线AB的距离.
设F1F2=x, 考虑梯形E1E2F2F1, 可得E1E2__=x+msinθ, 根据勾股定理:EE2=FF2=原问题转化为求解函数f(x) =的最小值问题.
显然可得f(x) 为增函数, 当x= 0 时,f(x) 取到最小值为接下来, 固定点E,F, 移动点A,B, 同理可得在相同的状态下取得表面积的最小值.三棱锥A −BEF表面积的最小值为:
根据上面总结的模型,我们可以编制出如下的变式供读者练习:
变式4如图9-1, 在长方体ABCD −A1B1C1D1中,AD=2,AB=BB1=1,线段B1D1上有两个动点E,F,且EF= 1,求三棱锥A −BEF表面积的最小值.

图9 -1
变式5如图9-2, 在长方体ABCD −A1B1C1D1中,AD=2,AB=BB1= 1, 线段B1D1上有两个动点E,F, 且EF= 1,线段AB上有两个动点P,Q, 且求三棱锥P −QEF的体积.
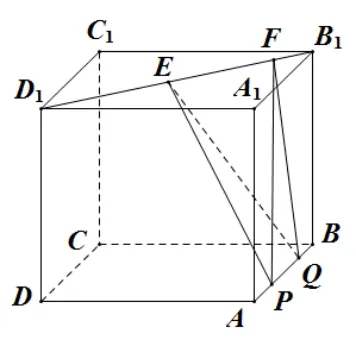
图9 -2
变式6如图9-3,平行六面体ABCD −A1B1C1D1的体积为2,底面ABCD为矩形,AD= 2,AB=BB1= 1, 线段B1D1上有两个动点E,F, 且EF= 1,线段AB上有两个动点P,Q, 且求三棱锥A −BEF的体积.
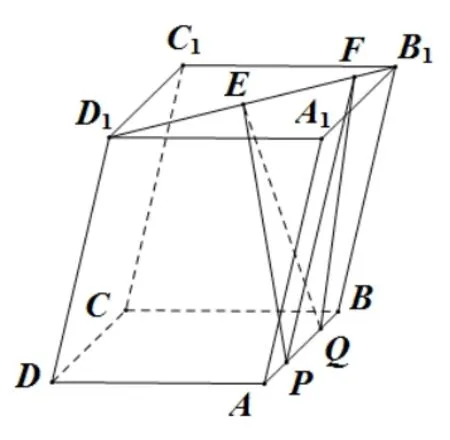
图9 -3
四、应用该模型
例1(2020 届佛山二模第11 题)已知A,B,C是球O的球面上的三点,∠AOB=∠AOC=60◦,若三棱锥O−ABC体积的最大值为1,则球O的表面积为( )
A.4πB.9πC.16πD.20π
分析本题的常规解法是选择恰当的基本量,选择合适的底面与高.本题若选择以C为顶点, 对应的计算量较小.若选择以点O为顶点,则对应的计算量较大.本文通过上面总结的模型进行求解,直击问题的本质.
解析如图10, 考虑异面直线OA与BC, 设球O的半径为r,则有OA=r,BC为2x.设直线OA与BC间的距离为h, 结合图形的对称性可知,设AC,OB的中点为E,F, 则有h=_EF,根据上文总结的模型可知VO−ABC=根据基本不等式:当且仅当x=时, 等号成立.对应的体积的最大值为VO−ABC== 1,由此可得r= 2,对应的外接球的表面积为16π.
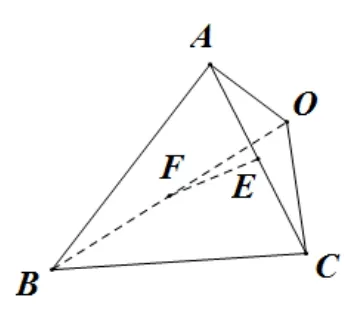
图10
例2(2020年安徽省“江南十校”综合素质检测第12题) 如图11, 在平面四边形ABCD中, 满足AB=BC,CD=AD,且AB+AD=10,BD=8,沿着BD把ABD折起, 使点A到达点P的位置, 且使PC= 2, 则三棱锥P −BCD体积的最大值为( )


图11
解析根据上面的模型, 选择异面直线BD,PC进行求解.设异面直线BD,PC之间的距离为h, 夹角为θ=则有VP −BCD=·PC·h·sinθ=原问题转换为求异面直线BD,PC之间距离的最大值问题.如图12,设PC,BD的中点分别为E,F,连接EF.

图12
根据异面直线间距离的定义可知:h≤EF.连接CF, 根据图像的对称性易知∆CEF为直角三角形, 可得考虑∆BCD,根据极化恒等式以及基本不等式可得当BC=CD=5 时,CF取到最大值3.由此可知EF的最大值为容易证得此时EF恰好为PC,BD的公垂线.由此可知h的最大值为则三棱锥P −BCD体积的最大值

