一道零点个数问题的解法探究

广东省惠州市第一中学 (516007) 黄伟才

题目函数f(x)=axex+lnx+x(a∈R).

(1)若a≥0，试讨论函数f(x)的单调性；

(2)若f(x)有两个零点，求a的取值范围.

本题是广东省珠海市2018届高三3月质量检测理科的压轴题，表述简洁，蕴含着丰富的数学思想，是一道入口宽，通法多的好题，全面考察了学生的导数与应用知识，还有函数与方程、化归与转化和数形结合等重要思想.这道题恰恰也是2017年全国I卷21题的改编题目，改后解法更丰富，且能更好考查学生对导数应用知识的掌握，所以笔者认为此题契合了全国卷命题风格，是一道以能力为立意的好题.本文谈谈我对这道题的一些思考，希望对读者有所启发.

一、解法探究

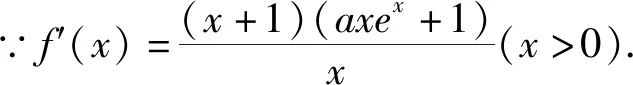
(1)若a≥0，易知f(x)在(0,+∞)单调递增.

(2)∵f(x)有两个零点，由(1)可知a<0，令g(x)=axex+1(x>0)，则g′(x)=a(1+x)ex<0，∴g(x)在(0,+∞)上单调递减.∵g(0)=1>0，

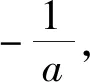
以上含参取点问题，应用分析法，执果索因，思路自然，所用思想方法易于理解，更能有效培养学生的分析问题、解决问题的能力及逻辑推理核心素养.

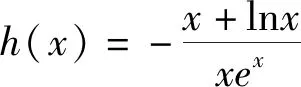
赏析2：当含参分类讨论较复杂时，可以用分离变量来去避免讨论，但要学生熟练掌握函数极限的判断，甚至还要用到洛必达法则，这个中学数学教师特别喜爱的定理，可是由于高中阶段洛必达法则没有引入，所以高考中究竟如何才能拿满分还值得商榷.

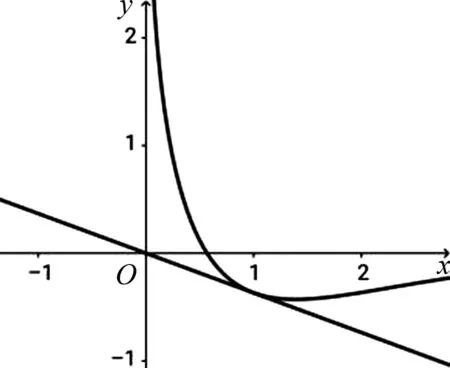
图1

解法3：(局部分离参数)f(x)有两个零点，可转化为函数m(x)=

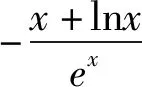
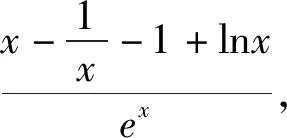
赏析3：合理分离构造函数，把函数零点问题转化为两个函数图像交点问题，不过这类问题最好转化为一次函数和非线性函数的交点问题，结合单调性和求切线可以顺利解决，这里需说明所分离的函数图像凹凸性才更加严谨.若要证明f(x)没有零点，则还可以合理分离lnx和ex，构造非线性函数，利用函数凹凸反转证明没有交点，解题思想如2014年课标Ⅰ卷理科21题第2问.

赏析4：这道题目入口之宽的精妙之处在于此，居然还可以用对数恒等式，等价转化为复合方程解的个数问题.笔者姑且大胆猜测命题者编题是先由f(t)=aet+t零点个数，再令t=x+lnx，把原本简单的问题通过对数恒等式包装隐藏起来，进而得到函数f(x)=axex+lnx+x零点个数问题，变成一道难度极大的压轴题.

二、教学启示

从上述4种解法可以发现，本质上要用导数来研究函数图像的形态，过程会涉及到分类讨论，零点定理，隐零点问题，函数不等式比较大小，数形结合及合理分离构造函数等思想方法.当然本题还给笔者留下了如下启示：

1.回归教材 正本清源

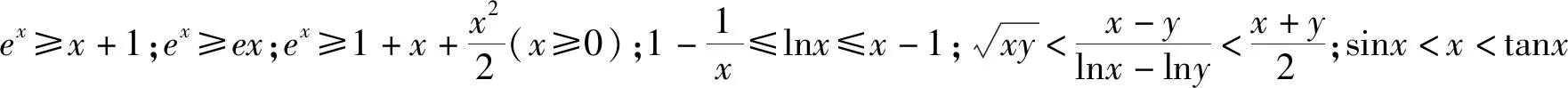
2.引导学生从一题多解过渡到多题一解