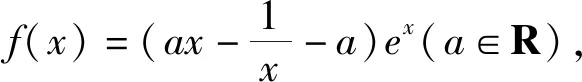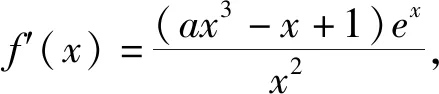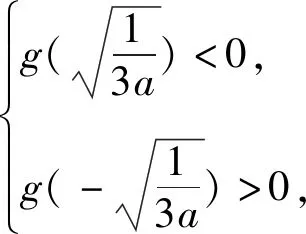巧定“界点”妙讨论:导数解答题的破解策略
重庆市璧山中学 (402773) 杨 帆
导数解答题是历年高考数学中重点考查的数学题型之一,经常作为压轴题形式出现,其主要特点是思维量大、运算繁琐、区分度高开.而其求解往往离不开对参数的分类讨论,如何巧妙确定分类讨论的“界点”,是成功破解导数问题的策略所在.本文结合实例,就常见的几类巧定“界点”方法加以剖析.
1.巧借二次项系数,妙定讨论“界点”
例1 (2021届“决胜高考”高三新高考八省第一次模拟测试题)已知函数f(x)=lnx+ax(a∈R).
(1)当a=-2时,求函数f(x)的极值;
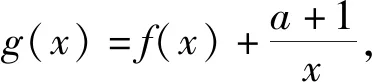
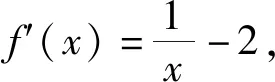
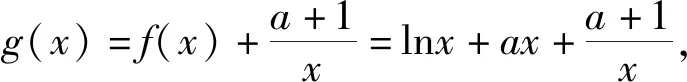
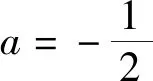
评注:涉及的导函数中含有二次三项项,需要对最高项的系数进行分类讨论,根据二次项系数是否为0,判断函数是否为二次函数;由二次项系数的正负,判断二次函数图象的开口方向以及相应的特征,从而寻找导的变号零点,为分类讨论的“界点”确定定下基调.
2.巧借判别式,妙定讨论“界点”
例2 (2019年武汉外国语学校模拟题)已知函数f(x)=(1+ax2)ex-1(a∈R),其中e为自然对数的底数.
(1)当a≥0时,讨论函数f(x)的单调性;
(2)求函数f(x)在区间[0,1]上零点的个数.
解析:(1)f′(x)=(ax2+2ax+1)ex,当a=0时,f′(x)=ex≥0,此时f(x)在R单调递增;当a>0时,判别式△=4a2-4a.
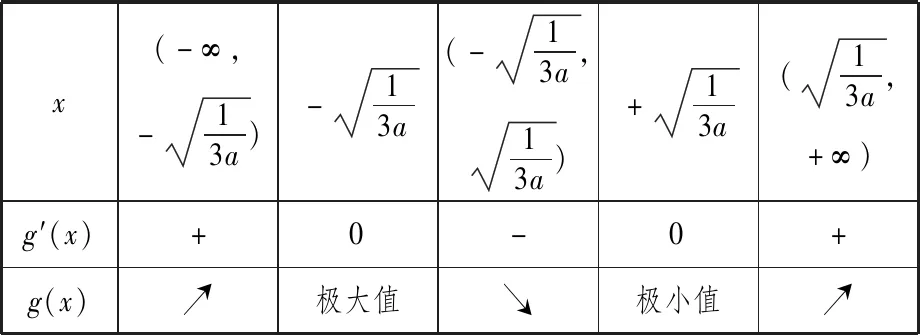
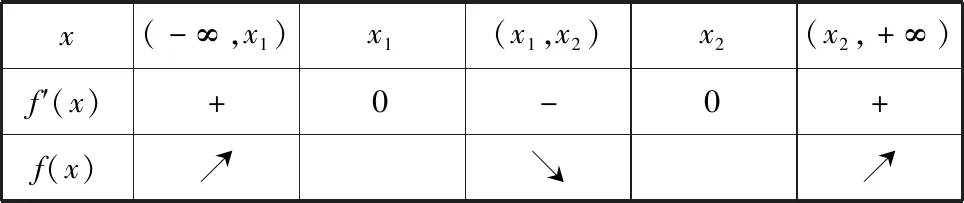
①当0 x(-∞,x1)x1(x1,x2)x2(x2,+∞)f′(x)+0-0+f(x)↗↘↗ 评注:通过对涉及函数进行求导,要判断导函数是否有零点(或导函数分子能否分解因式),特别在导函数是二次函数或与二次函数有关的问题时,此时涉及二次方程问题就要结合判别式△与0的大小关系来分析,利用这个关系讨论的“界点”进行分类讨论. (1)当a=0时,求函数f(x)的单调减区间; (2)已知函数f(x)的导函数f′(x)有三个零点x1,x2,x3(x1 列表如下: x(-∞,-13a)-13a(-13a,13a)+13a(13a,+∞)g′(x)+0-0+g(x)↗极大值↘极小值↗ 由于g(x)有三个非零的零点,所以 评注:根据导函数的零点来确定分类讨论的“界点”时,一定要在函数的定义域内加以分析.借助导函数的零点划分对应的函数定义域,既要考虑导函数零点是否在定义域内,还要考查多个零点的大小问题,如果多个零点的大小关系无法确定,也需要进行分类讨论. 实际上,分类讨论破解导数问题中,“界点”的确定变化多端,只有抓住这几类常见类型,灵活多变,合理转化,综合运用分类讨论思想,巧妙通过导数求解函数的单调区间、参数范围、极值、最值以及恒成立等才能将问题顺利求解.
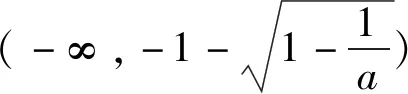
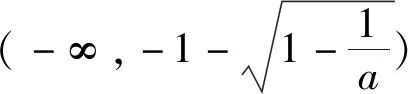
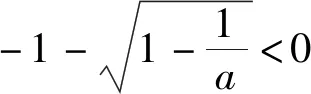
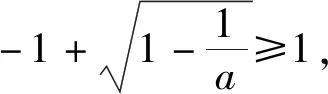
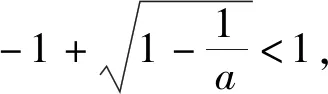
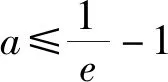
3.巧借导函数零点,妙定讨论“界点”