两道教师解题比赛题的优解

江西省玉山一中 (334700) 陈 虹

近日，笔者参与了上饶市首届高中数学解题讲题大赛，认真钻研了这份试卷，认为试题新颖独特，内容覆盖面广，质量优秀，解法灵活.本文就其中两道题的解法进行了优化.

例1 如图1，在△ABC中,角A,B,C所对的边分别为a,b,c,且满足(2b-c)cosA=acosC,D是BC边上的一点.

图1

(1)求角的大小;

命题者的解法：(1)由(2b-c)cosA=acosC可得

(2sinB-sinC)cosA=sinAcosC，2sinBcosA=

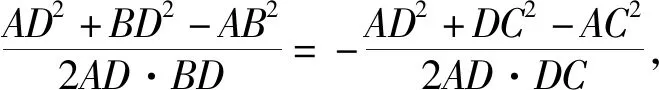
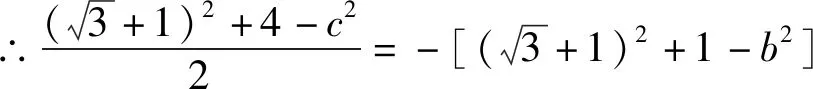
上述第(2)问的解答是通过一对互补角，结合余弦定理建立b,c的关系式，化简过程三次使用余弦定理，然后再转化为b,c关系而求解.此法化简过程繁琐，并且解二元二次方程组计算量大.如果采用向量数量积和余弦定理相结合的方法，通过配方、换元等大家熟练掌握的技巧将二元二次方程组转化为一元二次方程求解，就会使得解题过程显得简单易算.

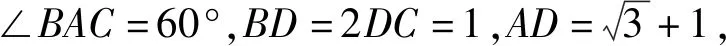
例2 已知函数f(x)=ex+sinx+cosx-a(x+1)≥0对任意x∈[0,+∞)恒成立，求实数a的取值范围.

命题者的解法：由题意f(0)=2-a≥0，所以a≤2.下面证明当a≤2时题目成立.

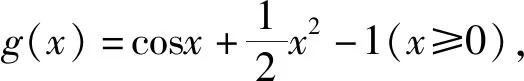
以上解答用到了泰勒展开式，并构造了三个函数，已超出了初等数学范围，并使问题过于复杂化.本题如运用常见不等式“x≥0时sinx≤x”进行合理放缩，则能有效地优化其题解法：

优化解法：由题意f(0)=2-a≥0，得a≤2.下面证明当a≤2时命题成立.即证f(x)=ex+sinx+cosx-2(x+1)≥0对任意的x∈[0,+∞)恒成立.