开发内隐性课程资源 提高课堂教学有效性
——函数单元复习课的改进与思考
江苏省无锡市立人高级中学 (214161) 郑宝生 张小荣
一、问题的提出
南京师范大学喻平教授认为,数学课堂教学的课程资源有外显性和内隐性,而内隐性资源又可以区分为内隐素材性资源和内隐条件性资源,内隐素材性资源是指不以文本形式显性表述的,潜藏于显性知识深层的隐性知识,它包括数学知识的文化元素、过程元素、逻辑元素和背景元素.按照2017年版普通高中数学课程标准:“数学文化是指数学的思想、精神、语言、方法,以及他们的形成和发展,还包括数学在人类生活、科学技术、社会发展中的贡献和意义,以及与数学相关的人文活动”.内隐条件性资源是指教师对素材性资源的理解,结合外显条件性资源构建的一种适宜于学生学习的课堂环境,它包括构建学生智力和非智力因素共同参与的学习情境,营造平等的课堂对话氛围,使用有效的方式提出问题等.
前一段时间,区里的名师工作室开展了一次教研活动,一个青年教师上了一节公开课,内容是高一数学的“函数单元复习”,所用教材是苏教版《普通高中课程标准实验教科书·数学》必修1.由于教材中没有这一节的具体内容,需要教师根据前面的教学内容和学生的实际情况来决定教什么?怎么教?对于青年教师来说是一种严峻的考验,他们需要整体把控本单元内容,确定哪些是重点和难点?怎样才能真正地体现学生的主体作用?等一系列问题.课后进行了集体评课,有的教师提出了一些中肯的建议,也有的教师给出了改进的方法.从课程资源的角度,这节课需要开发出哪些内隐性课程资源,才能使课堂教学更有效?
二、 教学片段
片段一:课前热身
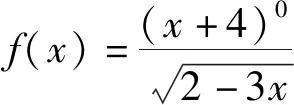
题2 已知函数f(3x)=2x2+1,则函数f(x)=;
题3 已知函数f(x)是定义在R上的偶函数,且在[0,+∞)上是增函数,则不等式f(x+1) 学生比较容易解答上述问题,在师生平和的对话中澄清了每一个细节,气氛活跃且融洽,学生有较高的参与度.接下来,教师让学生回忆函数定义、表示和性质(如图),虽然教师的板书简练清晰,很好的完成了单元复习所要完成的知识网络建构.但是,知识网络的建构与前面学生解题体验关联不大,不能融为一体,导致在知识网络建构的过程中学生的参与度明显降低,大部分都是教师独自完成. 如果要改进的话,教师应该让学生对解答的三个问题进行反思,我们都用到了哪些学过的知识?再让学生对函数的定义、函数的解析式、函数的定义域和法则,以及函数的单调性和奇偶性等,这些散乱的知识按照一定的关系进行梳理.这样的问题答案并不唯一,学生的思考有较大的自由度,更好地体现学生的自主性,发展学生思维的逻辑性,培养学生有条理的操作能力. 片段二:拓展衔接 由于执教者没有给学生深入思考的时机,而是匆忙进入下一个环节——典型例题,丧失了一个调动学生积极性,并充分发挥学生主体作用的机会.只要教师提出:对于上面题1和题2两个问题你还能求什么?等于给学生搭建了一个有情境限制无思想束缚的自由平台,让学生更好地发现问题.我们难以预测学生会提出怎样的问题,但是教师必须事先做好预案. 意图:从求具体函数的定义域上升到求抽象函数的定义域. 意图:一方面能更好地反馈学生对函数概念的理解,另一方面也可以确认怎样的分段函数图像是单调减函数,怎样的不是单调减函数,为后面的“典型例题”做好知识储备,让开头的问题与后面的例题有一个更好的衔接. 接着教师再提出如下问题:对于开头的题3你能把它们的条件用其它的数学符号语言来表述吗? 题6 (1)f(x)是偶函数可表示为:①任意的x都有f(x)-f(-x)=0;②任意x、y都有f(x+y)=f(x)-f(y); (3)由于函数f(x)是定义在R上的偶函数,且在[0,+∞)上是增函数,可表示为f(x)=x2|x|. 意图:尽可能让学生去联想、去发现,给学生一个展示自我的舞台,这种问题条件的渐近式变化,在变化中体现不变的数学本质,有利于学生的理解和掌握,并体悟到数学中变与不变的趣味以及出题者的用意和思维方式. 以上只是备选方案,要根据学生的实际情况斟酌选用.对于高一的学生来说,不能让例题过于冷僻,学生的学习能力是在潜移默化中成长起来的,拔苗助长只能适得其反.通过对函数奇偶性和单调性的变式处理,体现了函数这个单元中的重点知识,化解了函数中的难点内容,为后面的函数学习搭建一个脚手架. 片段三:典型例题 执教者所选用的例题如下: 例1 (1)若函数f(x)= (2)已知函数f(x)=|x-4|+|x+4|,解不等式f(x2-3)>f(2x). 例2 函数f(x)的定义域为R,且对任意的x、y∈R,都有f(x+y)=f(x)+f(y),当x>0时,f(x)<0,且f(1)=-2. (1)证明:函数f(x)是奇函数; (2)证明:函数f(x)在R上是减函数; (3)求函数f(x)在区间[-3,3]上的最大值和最小值. 课堂的实际情况是:例1的第一小问,学生还是能够参与其中的,但是有大部分学生没有考虑x=-1时函数值大小问题,导致解答错误;对于第二小问,学生能够参与解答f(x)的奇偶性,也能正确地脱去绝对值,画出函数f(x)的图像,但是解不等式f(x2-3)>f(2x)学生就无从下手了,教师只能自己讲,学生听的有点糊涂,其效果并不理想,例2也就没有时间去处理,只能草草收兵. 课后,工作室里的教师从学生参与课堂教学的角度进行研讨,大家一致认为:例1的第一问之前,需要让学生对分段函数是减函数的图像有一个清晰的认识,学生能够区分是减函数的分段函数图像和不是减函数的分段函数图像.这样学生参与解答例1第一问的主动性会更高,不考虑x=-1函数值的学生会更少.其次,对于例1第二问,在本节课的教学时机并不成熟,虽然课前热身题3已经做了铺垫,在偶函数f(x)中,f(x+1) 要提高课堂教学的有效性,需要关注“教什么?”的前提下,也要关注“怎样教?”,既要重视外显性课程资源的利用,也要重视内隐性课程资源的开发. 1.建构课堂的学习情境 强化学生的主体地位 学习情境是一种内隐条件性课程资源,既有智力因素方面的问题情境,又有非智力因素方面的学生参与的态度和情感.只有学生的主动参与和积极思考,形成平等的课堂对话氛围,才能真正提高课堂教学效益.本节课开头的三个问题从知识的角度讲,涉及函数的定义域、求函数解析式以及利用函数的性质,涵盖了函数这一章的主要内容;从课堂教学实际来说,师生的交流自然且有思维含量,学生的学习热情高、参与面广,说明了构建这样的学习情境还是恰到好处的.其次,在改进的环节二是本节课的核心,它承接环节一的三个小问题,从知识的角度讲是为环节三搭建了脚手架;从过程的角度看,学生在参与中能得到一种情感体验,有了这样的体验才能够转化为经验,其目的是为环节三构建一个有效的学习情境,使学生在环节三中能自主地思考、独立地解决问题,真正体现学生的主体地位. 2.展示数学文化元素 体现数学知识的思想性 数学所具有的抽象性、严谨性和广泛性展示了数学文化的力量.然而,在数学形成和发展中所体现出来的数学思想方法,对人的思想观念的感化和影响是潜在的,也是巨大的.在改进后的课堂教学,更强化了数和形的思想方法,在环节二的题5中,让学生用一个二次函数和一个一次函数组成一个分段函数,使这个函数是单调函数,这种开放性的问题能更好地反映学生在形上感知单调函数,从而体会函数单调性定义在数与式中的意义.其次,环节二的题6给出了各种变式,呈现的是函数单调性各种符号的不同表征,其解决方式都是回到函数单调性定义中去,体现了问题解决过程的化归思想.最后,环节一的题3、环节二的题4以及环节三的例2都是使用的抽象函数,三个题目是渐进式且有一定的梯度,体现了数学抽象的思想,能更好地培育学生的理性精神. 3.挖掘数学的逻辑元素,培育学生的逻辑思维能力 逻辑泛指规律,包括思维规律和客观规律.我们通过数学知识的客观性来培育学生思维的逻辑性,通过数学知识的主观性来锻炼学生的逻辑思维能力,使学生的思维更合情、合理、合规.在环节一中,需要学生通过自主练习后的反思,提取所用的知识点,并建立起一定的知识网络结构,关键在于学生的主动参与、积极建构,才能够更好地完善学生的知识结构,促使学生合理地思考、清楚的表达、有条不紊的工作.其次,环节三中的例2是一个简单的代数推理,学生要独立完成,就需要具备一定的逻辑推理能力.最后,三个环节之间,前面的环节是后面环节的知识基础,而后面环节是前面环节的推广或综合,小步推进逐渐提升,充分体现了各环节之间的逻辑性和秩序性,在潜移默化中也能影响学生的逻辑思维能力的提高.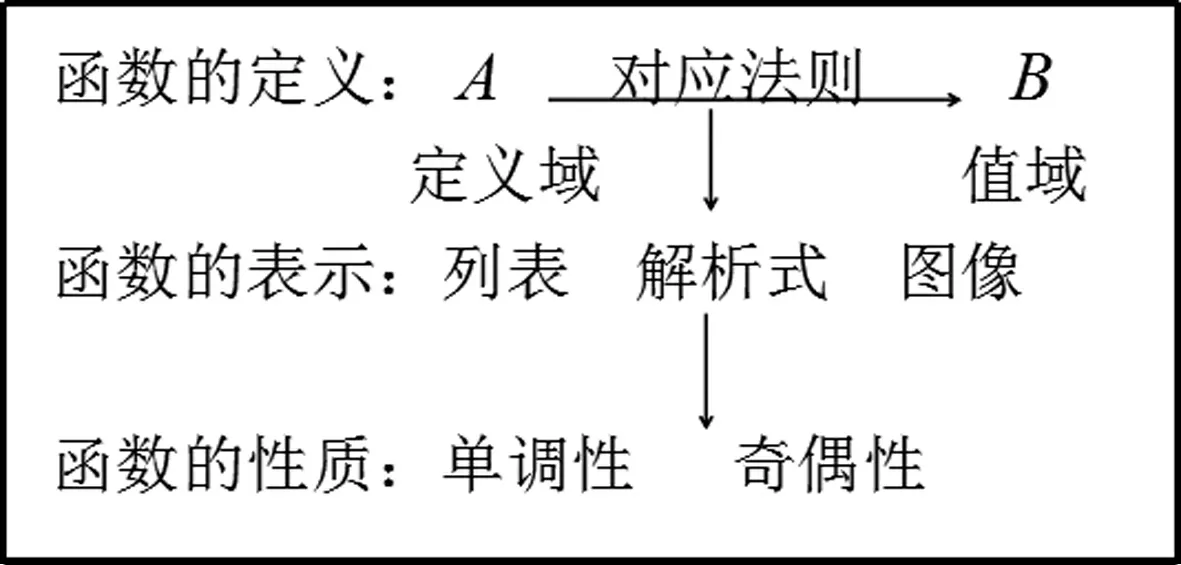
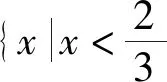
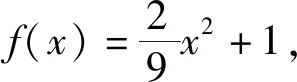
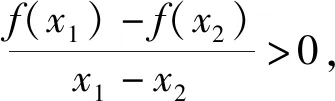
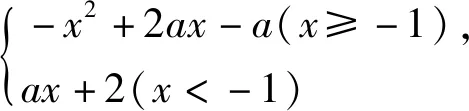
三、教学感悟

