再谈高中学生数学说题

福建省南安市教师进修学校 (362300) 陈俊斌

近日我市在市教师进修学校举行南安市首次中学生数学“说题”交流评比活动，比赛分初中组和高中组，比赛时间为每位学生8分钟以内. 参赛学生通过事先学习提供的“中学生数学说题活动”的资料，对学生说题的流程及框架有所了解, 比赛现场精彩纷呈. 现笔者结合本市开展的中学生数学说题比赛及教研实践谈谈对中学生数学说题的思考与认识.

1 数学说题

数学说题是指说题者在精心解题的基础上，面对被说题者，阐述对试题的知识内涵、能力要求、思想方法、拓展变式、反思总结等方面作出解说，以口头表达为主，以数学思想方法为依据，以问题本身涉及的知识内涵为基础的一种教研活动.也就是把审题、分析、解答和回顾等思维过程按一定顺序说出来的一种教研展示活动.从说题主体来看，说题可分为教师说题、学生说题、教师和学生互动说题,本文主要研究学生说题.

2 学生现场说题

指学生在解完一道题后，向教师或专家评委等，阐述自己解决试题的思维暴露过程.学生通过说题，能举一反三，学会解一类题.学生说题主要包含如下几个环节：一是理信息，说审题，即运用数学语言分析题目所给的信息，已知条件有哪些，所求结论是什么，题目涉及哪些知识点;二是析条件，说思维，说解题思路获得的全过程，即解决这道题目运用的什么方法，有哪些步骤，是如何想到的，如何表述，如何实践操作;三是微总结，说反思，即解完一道试题后，结合自己对整个问题思考的全过程进行微总结，即解决这道题都运用到哪些数学思想方法，有无其它解法，哪种思路最优、所得结论或性质是否具有规律性，能否进行推广？题目能否进行其它变化？

案例1 母题：已知x2+y2=1.求x+y最大值.

变式1已知x2+y2=1.求4x+y最大值.

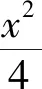
本题组为我市中学生数学说题交流评比活动中，南安一中高二学生采用的说题试题.考虑到是首次进行学生现场说题比赛，本次比赛我们采用由参赛者“自定题”，再进行现场说题的形式，时间为不超过8分钟.该生从试题再现与分析、试题变形、试题再变形、同类题解后反思等方面进行现场说题，现以此为例进行剖析.

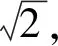
反思是对解题思维活动的反思，数学的理解要靠不断反思才能深化.本例中学生正是从一道试题解法入手，通过对试题进行简单的改编(更换结论，变更条件)，再从原题解法对改编题进行推广时遇到的困惑及处理办法，数形结合，步步反思，最终他得到解决该类试题的通法.

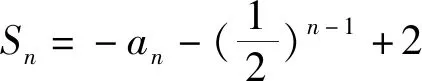
(1)令bn=2nan，求数列{bn}的通项公式；

3 学生课堂说题

指上课之前教师精选教学内容，全体学生精心备“说”；教学过程中，教师在适当的时间引导部分学生在课堂上进行“说题”展示，并在学生说题后进行及时的反馈和评价，其它学生则在教师的引导和学生“说题”展示的过程中积极主动地思考，并及时提出问题与困惑，师生共同解决.与学生现场说题不同的是，由于课堂时间有限，说题各环节无法一一展现，重在解题过程、解题思路获得的分析上，或者重点说有自己独特见解的方面，还要注意的是，最好让学生事先做题，与课堂讲题有所区别的是：这时的课堂说题重在思维的交流，思想的碰撞.

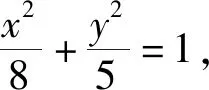
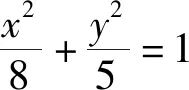
本例为我市在南安三中开展的现场课题观摩课《直线与圆锥曲线的位置关系》中，学生课堂说题的题目之一.该课授课老师采用学生课前自主探究问题，写出解答过程，课堂学生说题展示，教师点评反馈，全体学生带着问题交流、思考，力图通过课堂学生说题活动，展示他们对直线与圆锥曲线位置关系知识方法的掌握情况，暴露出学生在该部分知识上存在的问题，以便每位学生针对自己的情况及时进行弥补.以下还原部分学生在课堂上的说题实录.

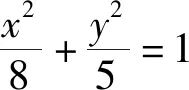
生1:那要判别位置关系，根据刚才老师复习的，我们可以联立方程然后用判别式求解.如果有2个解，就有2个公共点;如果有1个解，就有1个公共点;如果没有解，就没有公共点.刚才复习到直线与椭圆的位置关系，联立后方程二次项系数必不为零，所以有判别式.

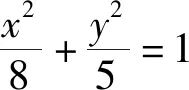
其余学生：掌声……

师：刚才××同学讲得很辛苦，好长啊！我们这个题目是等下对应另一种方法，所以才设计这么复杂的计算，其实运算应该比这个简单些，应该说我们××同学很有意志力(学生笑声)……我昨天改作业，看到很多同学都算错了，(其实)是可以算出来的.

师：(kx-2k-1)2=[kx-(2k+1)]2=k2x2-2k(2k+1)x+(2k-1)2，可以用我们学过的完全平方公式解决.这里要注意下.在改作业的过程中，我们发现有同学没写过程(却)得出2个交点的，下面我们请他上来说说.

生2：直线是y=kx-2k-1 ,(台下学生笑声)，写出点(2,-1) ，并画出直线与椭圆的草图，然后把x=2代进去，y=?(站着思考一会儿，说不出所以然)，所以(2,-1)在椭圆内，直线过椭圆内一点，所以有2个交点.

师：××同学意思没说清楚，他是说看出直线y=kx-2k-1过定点(2,-1)，(那么)我们是如何看出直线y=kx-2k-1是过定点的？把y=kx-2k-1化成y=k(x-2)-1即可发现，当x=2时，y=-1，所以其实在分析这个问题的时候，我们就应该可以看出这条直线的几何特征.这里，能否看出该直线过定点很重要.

师：解析几何的问题常见有两种类型：一是根据曲线方程研究曲线的性质，一是根据已知条件求曲线的方程.这里，我们作出图形后，可以看出点(2,-1) 在椭圆内，怎么判断呢？

生3：代入……

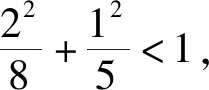
总之，学生说题，是一种交流，也是一种学习方法.通过学生说题，能暴露出他们面对数学试题的思维过程，并通过把课堂内外所学知识与自身数学学习实践相结合，从解一道题到解一类题，举一反三，掌握所说试题的数学本质.开展学生“说题”比赛，能培养他们良好的思维习惯、提升学生思维品质，提高学生的解题能力，让学生养成“想题、做题、反思、说题”的学习习惯，提高学生的数学素养；学生说题，也有利于转变教师教育教学观念，更充分调动学生学习数学的积极性，培养他们敢于探索和主动创新的精神.长期坚持学生说题，必定能提升学生的口头表达、数学交流的能力，从而促进其思维能力的发展.