2类图1-因子数的计算公式*

唐保祥, 任 韩

(1.天水师范学院数学与统计学院,甘肃 天水 741001；2.华东师范大学数学科学学院, 上海 200062)

研究图的1-因子的计数问题，具有重要的理论价值和现实意义[1-3]，该问题已经被证实是NP-困难问题.分类嵌套递推方法，是求解许多类图1-因子数的一种非常有效的方法[4-7].笔者拟构造2类新图mTn和mKn,n,并用分类嵌套递推方法推导mTn和mKn,n不同1-因子的计数公式.

1 基本概念

定义1若图G有一个1-正则生成子图D,则称这个生成子图D为图G的1-因子.

定义2设图G是一个有1-因子的图,若图G的2个1-因子D1和D2中有1条边不同,则称D1和D2是G的2个不同的1-因子.

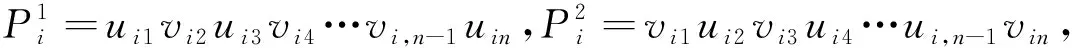
图1 图mTnFig. 1 Graph of mTn

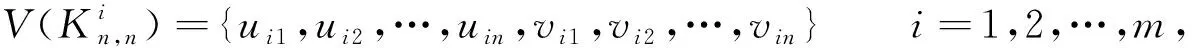
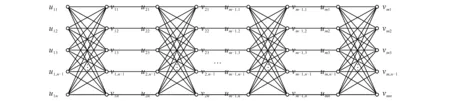
图2 图mKn,nFig. 2 Graph of mKn,n

2 主要结果及其证明

定理1设图mTn的1-因子数为σ(m,n),则有

图3 图

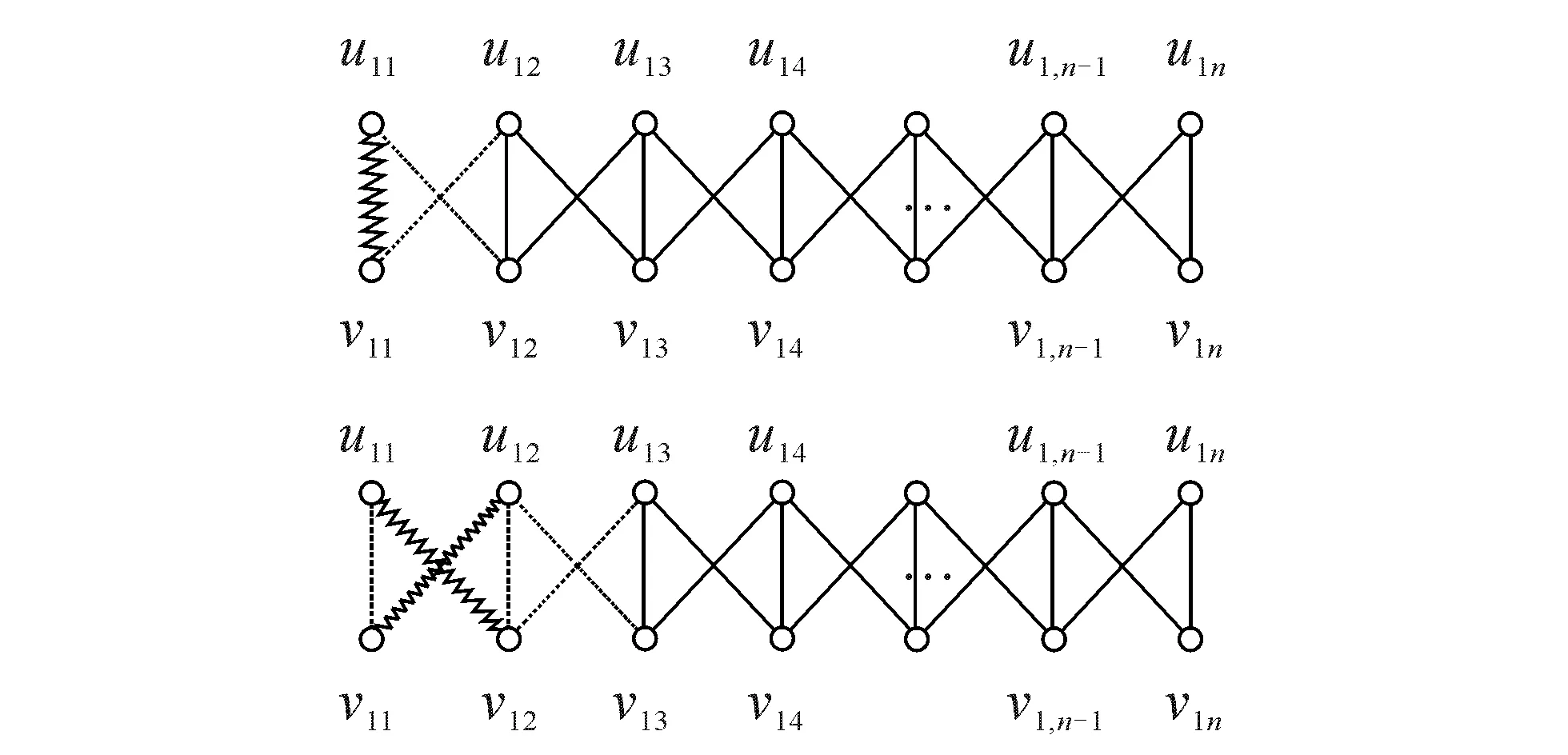
图4 图G1Fig. 4 Graph of G1

图5 图G2Fig. 5 Graph of G2

如图1所示,对于图mTn的任意一个1-因子D,若边u1jv1,j+1∈D(j≤n-1),则必须有u1,j+1v1j∈D.否则由u1jv1,j+1∈D可得u1,j+1v1,j+2,u1,j+2v1,j+3,…,u1,n-1v1n∈D,于是顶点u1n就不被1-因子D饱和,这与D是图mTn的1-因子矛盾.由此可知，图mTn的边vijui+1,j∉D(i=1,2,…m;j=1,2,…,n).

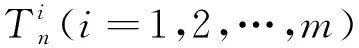
所以图mTn的1-因子数

证毕.

定理2图mKn,n的完美对集数τ(m,n)=(n!)m.

图6 图