兼具高自由度低互耦的间距约束稀疏阵列设计

岳世杰, 胡国平, 师俊朋, 周 豪, 占成宏

(1.空军工程大学防空反导学院，西安，710051；2.国防科技大学电子对抗学院，合肥，230000)

阵列信号处理因其优异的波束控制和空间分辨能力而在通信、雷达、声呐、导航等领域得到广泛应用[1-5]。由于存在测向模糊，传统阵列信号处理主要关注阵元间距小于λ/2的均匀线阵(uniform linear array，ULA)，N个阵元的均匀线阵理论上最多可估计N-1个信源[6]，随着信源数的增多，通常需要增加阵元数来满足测向需求，这就会相应增加硬件成本和计算复杂度。此外，传统均匀线阵由于阵元间距较小，阵元间存在较大的互耦，严重影响信源估计精度[7]。

稀疏阵列通过向量化协方差矩阵形成差联合阵列进而扩展孔径[8]，这为提高自由度、减小阵元间互耦提供了新的思路。早在1968年Moffet就提出了最小冗余阵[9](minimum-redundancy array，MRA)，虽然MRA能够提供最大连续差联合阵列，但由于这种阵型结构不存在闭式表达式，随着阵元数增多，需要大量计算来确定阵元位置，限制了MRA的应用。近年来提出的嵌套阵[10]和互质阵[11]因具有较大的孔径以及自由度的闭式解而引起学者的广泛研究。嵌套阵利用N个阵元得到O(N2)个虚拟自由度[10]，极大提高了测量精度和可估计信源数。互质阵阵元间互耦小，但是其差联合阵列形成的虚拟阵元不连续，因此得到的自由度往往不能充分利用。

在嵌套阵和互质阵的基础上学者们提出了改进阵列以进一步扩大孔径，减少互耦。文献[12]提出了阵元间距压缩互质阵(co-prime array with compressed inter-element spacing, CACIS)和子阵级联互质阵(co-prime array with displaced subarrays, CADiS)，CACIS压缩互质阵中一段子阵的阵元间距，虽然能够得到更大的连续虚拟阵列，但是CACIS中的最小间距元素间仍存在较大互耦，为克服互耦进而提出了CADiS，将一个子阵移到另一段阵列中，虽能减少互耦，但是其连续虚拟阵元要小于CACIS。文献[13]提出了将传统互质阵中一段均匀线阵的阵元数提升一倍的改进型互质阵，进一步提升了差联合阵列的自由度。文献[14]提出了改进嵌套阵(improved nested array)将传统嵌套阵的密集阵元的第1个阵元放到稀疏阵元之后，提升了嵌套阵的自由度，但是阵元间有着严重的互耦。文献[15]提出了二阶超级嵌套阵(second-order super nested arrays)，将嵌套阵的密集分布阵元放置在间距较大的阵元之间，在确保自由度的同时，减少了互耦。文献[16]在此基础上提出了Q阶超级嵌套阵(qth-order super nested arrays)进一步减少了阵元间的互耦。文献[17]将传统嵌套阵密集子阵分为4个部分，将其放置到均匀线阵的两侧，提出了增强嵌套阵，根据阵元分集的方式不同，提出了ANAI-1、ANAI-2、ANAII-1和ANAII-2。ANAI-1和ANAI-2虽能提升阵元自由度，但是无法显著降低阵元间互耦。

针对无法同时优化虚拟阵元孔径和阵元间互耦的问题，本文提出了一种间距约束稀疏阵列(inter-element spacing restriction array，ISRA)，该阵列基于约束阵元间距设计进而得到阵元位置，形成了4段以一定间隔首尾相连的均匀线阵。ISRA有自由度闭式表达式，且同时做到了自由度与互耦的同步优化，与相同阵元数的互质阵、嵌套阵、二阶超级嵌套阵等稀疏阵列相比，使用该阵列进行DOA估计效果更好，最后通过计算仿真验证了使用ISRA估计的有效性。

1 稀疏阵列回波信号模型

设有K个窄带远场不相干信号入射到由N个阵元构成的非均匀线阵，阵元位置分布在nid，其中ni∈Z，且S={ni,i=1,2,…,N}，d=λ/2，其中λ为信号波长。设K个信源入射角度为θ={θk,k=1,2,…,K}，则阵列回波信号模型为：

x(t)=As(t)+N(t)

(1)

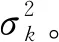
由x(t)可计算回波协方差矩阵为：

(2)

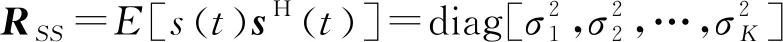
对回波信号协方差矩阵RXX向量化可得：

(3)

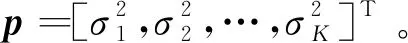
由A*∘A得到稀疏阵列虚拟阵元位置是实际阵元位置的差联合阵列[18]。

2 间距约束稀疏阵列结构设计

二阶超级嵌套阵是在嵌套阵的基础上将密布的子阵分解为六段尽可能稀疏的子阵，进而减少阵元间的互耦。ISRA设计借鉴二阶超级嵌套阵的设计思想，将阵列分为4段尽可能稀疏的子阵，并加入间距约束的思想，即除必须的一对阵元间距为d外，约束其他所有的阵元间距至少为2d并尽可能增大间距大于2d的阵元的数量。

如图1所示，给出ISRA结构，基于给定阵元数S，限制物理阵元之间的间距，进而确定物理阵元的位置。总阵元数为S=N1+N2+1，N1≥4且N1为偶数，N2∈Z+。该阵列由X1,X2,X3,X4这4段均匀线阵拼接而成。为减少阵元间互耦，则至少需要阵元间距为2d，因此约束两段均匀线阵的间距为2d，即阵元间距为2d，阵元数目为N1/2-1的均匀线阵构成的第一部分X1和阵元间距为2d，阵元数为N1/2-2的均匀线阵构成的第2部分X2；为进一步扩展阵列孔径，约束一段间距较大的均匀线阵，即由阵元间距为N1d，阵元数为N2的均匀线阵组成第3部分X3，N2≥1；为形成密布虚拟阵元，则至少需要有一段阵元间距为d，因此约束第四部分由阵元间距为d的2个阵元构成。约束X1,X2,X3,X4这4段均匀线阵之间的间距大于2d并通过调试得到这4段均匀线阵之间的间距分别为3d,N1d,(N1-3)d。通过约束各段均匀线阵阵元间距以及各段线阵之间的间距组成的ISRA能够形成连续的密布虚拟阵。

图1 ISRA阵元结构配置

令A表示为相邻阵元间距的集合，即A中第k个元素为第k个物理阵元和第k+1个物理阵元之间的间距。式(10)给出了阵元间距设置。假设参考阵元位于坐标轴0处，由相邻阵元间距确定阵元位置S。

(4)

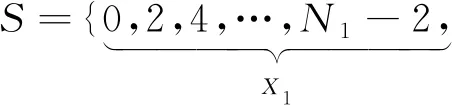
(5)

ISRA阵元位置是由N1，N2共同决定的，且总阵元数S=N1+N2+1，当给出S、N1、N2任意2个变量的值都能唯一确定集合A的值，进而确定阵元位置S。

3 间距约束稀疏阵列自由度

定理：ISRA的差联合阵列是密布均匀线性阵列，且该阵列的自由度为：

(6)

证明：

令X+={0,1,2,…,(N2+3)N1-6,(N2+3)N1-5}，为集合X中大于等于0的部分，令D+为差联合阵列D中大于等于0的部分，D代表ISRA阵元位置S的差联合阵列。则只需要证明ISRA的差联合阵列D=X。由权重函数[15]知X、D中元素关于0对称分布，则只需要证明D+=X+。

将差联合阵列的正向部分X+分为4个子集，分别为φ1={0,1,2,…,N1-1}、

φ2={N1,N1+1,N1+2,…,N1(N2+1)-2}、

φ3={N1(N2+1)-1,N1(N2+1),…,N1(N2+2)-5}

φ4={N1(N2+2)-4,N1(N2+2)-3,…N1(N2+3)-5}

定义集合和数字加减运算：

A±c={a±c|∀a∈A}

(7)

定义集合和集合的运算：

diff(A,B)={a-b|∀a∈A,∀b∈B,a>b}

(8)

设：

(9)

情形1：证明φ1⊆D+

显然{0,1}⊆D+

(10)

因为{N1-2,X1,N1+1}⊆S，则：

P1=

diff(N1-2,X1)={0,2,4,…,N1-2}⊆D+

(11)

P2=

diff(N1+1,X1)={3,5,7,…,N1+1}⊆D+

(12)

P1∪P2=

{0,2,3,4,…,N1-2,N1-1,N1+1}⊆D+

(13)

由式(10)～(13)得：φ1⊆D+。

情形2：证明φ2⊆D+

由{X1,X2,X3,2N1-3,(3+N2)N1-5}⊆S，

X3∪{2N1-3}={(2N1-3)+qN1|0≤q≤N2,q∈Z+}⊆D+，

P3=diff(X3∪{2N1-3},X1)=

diff(2N1-3,X1)+qN1=

{N1-1,N1+1,N1+3,…,2N1-3}+qN1⊇

{N1-1,N1+1,N1+3,…,2N1-3}+mN1

(14)

P4=diff(X3∪{2N1-3},X2)=

{0,2,4,…,N1-4}+qN1⊇

{N1,N1+2,N1+4,…,2N1-4}+mN1

(15)

P5=diff((3+N2)N1-5,{2N1-3}∪X3)=

diff((1+N2)N1-2,qN1)=

{N1-2,2N1-2,3N1-2,…,(1+N2)N1-2}⊇

{2N1-2}+mN1

(16)

其中：

0≤q≤N2,q∈Z+；0≤m≤N2-1,m∈Z+。

得P3⊆D+，P4⊆D+，P5⊆D+，P3∪P4∪P5⊆D+

又φ2⊆P3∪P4∪P5，则φ2⊆D+

同理可得φ3⊆D+,φ4=⊆D+。

综上可得：

X+=φ1∪φ2∪φ3∪φ4⊆D+

(17)

且max (D+)=max (S)-min (S)=(N2+3)N1-5，min (D+)=0。则：

D+⊆{0,1,2,…,(N2+3)N1-5}=X+

(18)

由式(17)、(18)得D+=X+。

证毕。

由定理知，ISRA的自由度是由N1和N2共同决定的，下面引理给出如何确定N1和N2的值才能获得最大的自由度。

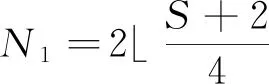
证明：

由定理知ISRA虚拟阵列满足X，且X中元素遍历所有在min (X)和max (X)之间的整数，则虚拟阵列自由度为DOF=max (X)-min (X)+1

设N1=2k，k∈Z+

DOF=2(N1(N2+3)-5)+1=

-8k2+4(S+2)k-9

(31)

表1给出了在已知阵元总数S的情况下ISRA的差联合阵列自由度。由表可以看出ISRA利用4r个阵元可以实现O(8r2)数量级的虚拟阵列自由度。

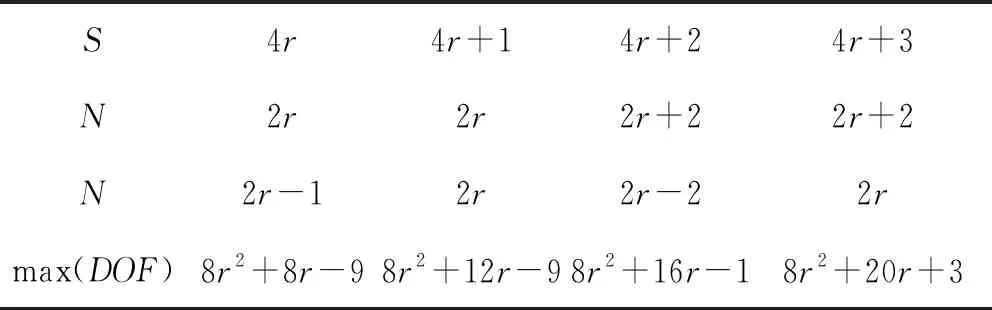
表1 ISRA配置

4 仿真实验

本节将通过仿真验证ISRA在减少互耦以及提高DOA估计精度方面的优势。仿真实验的计算机平台为Intel(R)Core(TM)i7-9750H CPU @ 2.60 GHz 2.59 GHz, RAM 8.00 GB，软件为Matlab(R2020a)。首先对比各稀疏阵列权重以及互耦率[15]，随后对比无互耦条件下DOA估计的均方值误差，最后分析阵元间存在耦合条件下不同阵列DOA估计的均方值误差。对于稀疏阵列，采用MUSIC算法[21]进行DOA估计。假设所有信源的功率相当且信源数一定，为了定量评价DOA估计结果，将归一化DOA估计均方根误差(共进行500次蒙特卡罗仿真实验)定义为：

(20)

4.1 权重及互耦矩阵

比较不同稀疏阵列与ISRA在阵列设计上的性能，表2给出了在不同阵元数情况下五种稀疏阵列的权重及互耦率。在表2给出的10阵元、15阵元、20阵元的情况下，嵌套阵和增强嵌套阵的权重ω(1)较大，而互质阵、二阶超级嵌套阵和ISRA保持着较低的ω(1)，且ISRA的权重ω(1)始终保持最低，为1，这反映了ISRA在这5种阵列中始终保持着较低数量的密布阵元。互质阵、二阶超级嵌套阵以及ISRA都保持着较低的互耦率，而嵌套阵和增强嵌套阵由于密布阵元较多而有着较高的互耦率。二阶超级嵌套阵和相同阵元数的嵌套阵拥有相同的虚拟孔径，但其互耦率要低于嵌套阵，这其中一部分原因是二阶超级嵌套阵在嵌套阵的基础上将密布子阵放置到稀疏的位置。ISRA的互耦率低于二阶超级嵌套阵，一方面是因为相同阵元数的ISRA自由度要大于二阶超级嵌套阵，另一方面ISRA通过间距约束使得权重ω(1)=1，减少了密布阵元的数量。

表2 5种稀疏阵列权重及互耦率对比

4.2 不考虑阵元耦合DOA估计

本节比较在无互耦的情况下，最小冗余阵、嵌套阵、互质阵、二阶超级嵌套阵、增强嵌套阵以及ISRA的DOA估计性能。设定阵元数为14，最小冗余阵阵元位置设定为[20]：

SMRA=

{0, 1, 2, 8, 15, 16, 26, 36, 46, 56, 59, 63, 65, 68}

(33)

对于嵌套阵以及二阶超级嵌套阵，设定N1=N2=7，互质阵按照文献[13]设定为M=4,N=7。

4.2.1 MUSIC空间谱

图2给出了不同稀疏阵列的MUSIC算法的空间谱，设共有50个信源均匀分布在[-80°,80°]，第k个信源的角度为：θk=-80°+160°(k-1)/49，其中1≤k≤50。设定信噪比为0 dB,快拍数为1 000。可以看出由于互质阵列的差联合阵列密布的阵元数目较少，不能有效分辨出50个信源。其余阵列均能有效分辨出50个信源，且可观察到最小冗余阵、增强嵌套阵以及ISRA的谱峰明显高于嵌套阵以及二阶超级嵌套的谱峰，这反映了最小冗余阵、增强嵌套阵以及ISRA在孔径上的优势使得角度估计的精度更高。

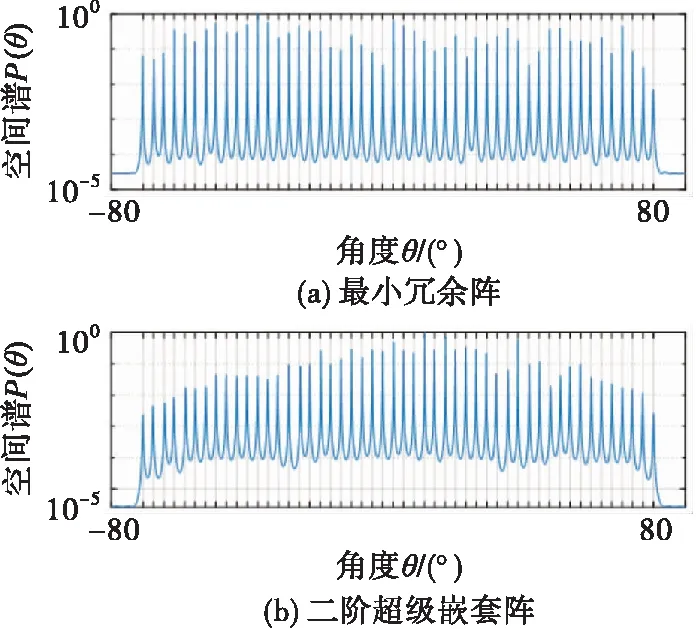
图2 不同阵列无互耦空间谱估计谱峰图

4.2.2 均方根误差

假设3个信源分布在-5°、0°、5°的位置。图3给出了均方根误差随信噪比增大的变化曲线，设定快拍数为1 000，信噪比从-30 dB以5 dB的步长增加到30 dB。从横坐标来看：信噪比小于-20 dB时所有阵列的均方根误差均较大，随着信噪比的增大均方根误差减小且最小冗余阵减小的速度最大，当信噪比大于10 dB时均方根误差趋于稳定。从纵坐标来看，当均方根误差趋于稳定时最小冗余阵均方根误差最小，互质阵的均方根误差最大，这是因为最小冗余阵有最大数目的连续虚拟阵元，而互质阵连续的虚拟阵元数目最小。ISRA和增强嵌套阵的估计效果略好于嵌套阵和二阶超级嵌套阵。

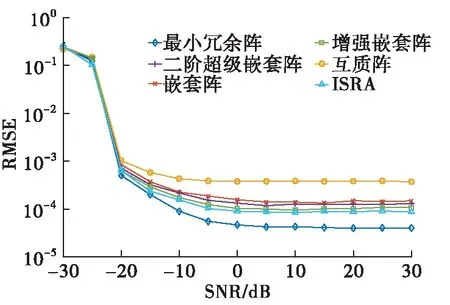
图3 归一化均方根误差随信噪比变化曲线

图4给出了均方根误差随快拍数的变化曲线，设定信噪比为0 dB，快拍数从10以300为步长增加到3 010。从横坐标来看，当快拍数小于310时所有阵列的均方根误差较大。随着快拍数的增大，均方根误差减小，在快拍数小于310时均方根误差减小的趋势最大，之后均方根误差减小的趋势减缓。从纵坐标来看，均方根误差趋于稳定后，最小冗余阵有着最小均方根误差，互质阵的均方根误差最大。ISRA和增强嵌套阵均方根误差相差较小，且略大于嵌套阵和二阶超级嵌套阵，这是由于ISRA和增强嵌套阵拥有相同大小的连续虚拟阵元，且ISRA和增强嵌套阵的虚拟阵元数目大于嵌套阵和二阶嵌套阵的虚拟阵元的数目。

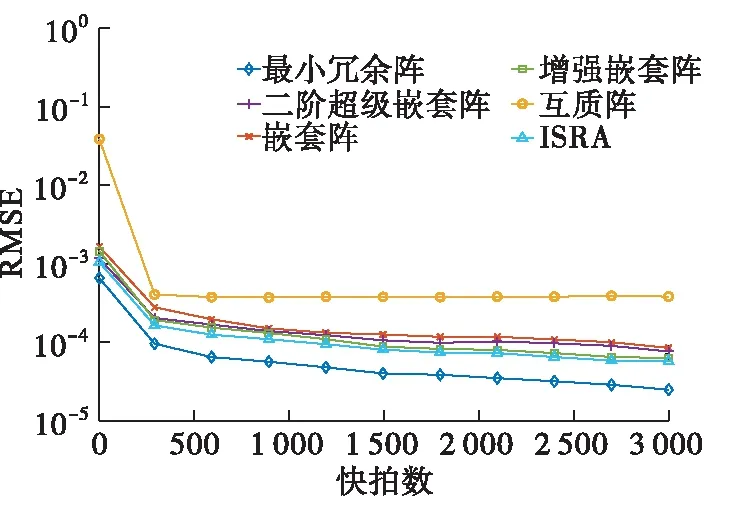
图4 归一化均方根误差随快拍数变化曲线

4.3 考虑阵元耦合DOA估计

本节考虑互耦对信源角度估计的影响，对比最小冗余阵、嵌套阵、互质阵、二阶超级嵌套阵、增强嵌套阵、ISRA的DOA估计性能。设定阵元数为14，阵元位置分布同4.2节。

4.3.1 MUSIC空间谱

设共有30个信源θk=-80°+160°(k-1)/29，其中1≤k≤30，信噪比为0 dB，快拍数为1 000，图5给出了有互耦影响下不同阵列谱峰图。可以看出所有阵列的空间谱的谱峰由于互耦影响都出现不同程度的削弱，但是ISRA仍能有效检测到30个信源；最小冗余阵、嵌套阵以及增强嵌套阵由于互耦在一个角度区间内出现多个谱峰；其余阵列则缺失谱峰或者谱峰偏离真实信源角度过远。

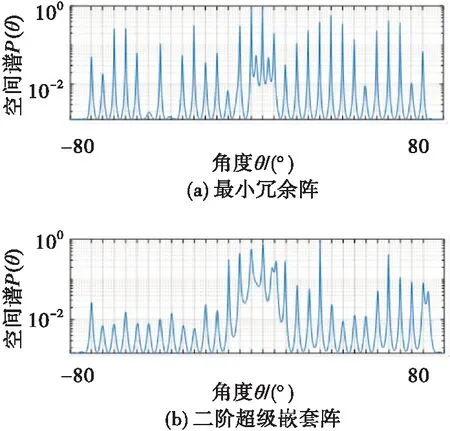
图5 不同阵列互耦影响下空间谱估计谱峰图

4.3.2 均方根误差

假设3个信源分布在-5°、0°、5°的位置。设定快拍数为1 000，信噪比从-30 dB以5 dB的步长增加到30 dB。图6给出了归一化均方根误差随信噪比变化曲线。从横坐标来看，当信噪比小于-20 dB时，阵列的均方根误差较大，随着信噪比的增大均方根误差减小，并在大于0 dB之后趋于稳定。均方根误差随信噪比减缓的速度在小于-20 dB时最大。从纵坐标来看，当均方根误差趋于稳定后嵌套阵的均方根误差最大，这是密集子阵互耦带来的影响。ISRA均方根误差最小，与最小冗余阵相比，虽然ISRA的自由度要小于最小冗余阵，但是ISRA受互耦影响更小，这就使得ISRA的估计效果要好于最小冗余阵。

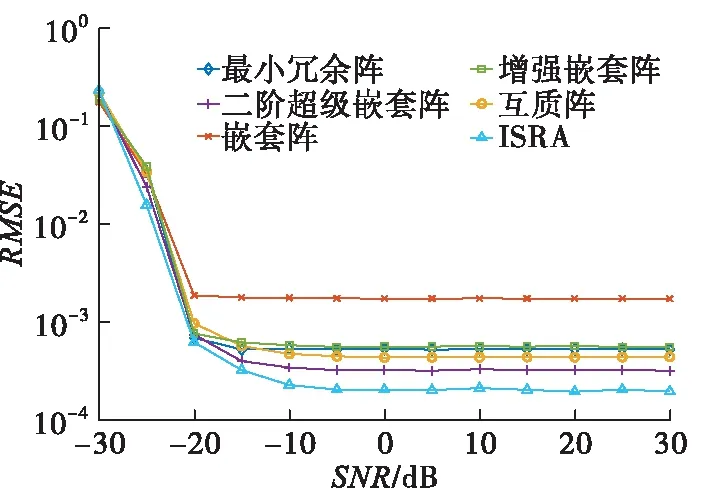
图6 归一化均方根误差随信噪比变化曲线

图7给出了均方根误差随快拍数的变化曲线，设定信噪比为0 dB，快拍数从10以300为步长增加到3 010。从横坐标来看，在快拍数较小时，阵列的均方根误差较大，随着快拍数的增大均方根误差趋于稳定。从纵坐标来看，均方根误差趋于稳定后，ISRA的均方根误差最小，嵌套阵的均方根误差最大。其余阵列的均方根误差由小到大依次是二阶超级嵌套阵、互质阵、最小冗余阵和增强嵌套阵。可得最小冗余阵和增强嵌套阵虽然有着大的连续虚拟阵元数目，但是互耦的影响使得他们的估计效果仍不理想。

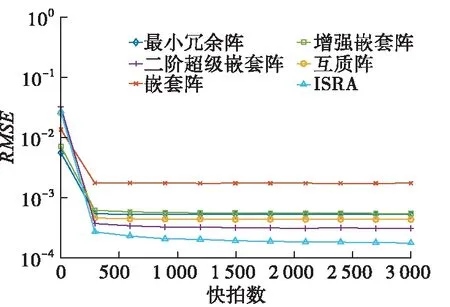
图7 归一化均方根误差随快拍数变化

5 结语

本文设计了一种兼具高自由度与低互耦率的间距约束稀疏阵列，该阵列给定阵元数量后即可唯一确定阵元分布位置以及差联合阵列的自由度。理论分析表明，该阵列的差联合阵列是无孔阵列，与嵌套阵、超级嵌套阵相比拥有更大的自由度；与互质阵、最小冗余阵和增强嵌套阵相比拥有更小的互耦。最后通过仿真验证了该新型阵列在测向方面的优越性。