连续批加工过程中嵌套自相关数据的控制图设计

陈昌华，李敬敏，姚 进,

（四川大学a.工商管理学院；b.制造科学与工程学院，成都610064）

1 问题的提出

在批加工过程中，工艺参数往往呈现嵌套性的特点。例如，对于晶片涂胶这类逐片批加工工艺，每片晶片上的胶膜厚度服从一定的分布，一般为正态分布。设其均值为μd，标准偏差为σd。而连续加工的若干片晶片之间，每片晶片上的均值μd又遵从另一个正态分布，这是最简单的一阶嵌套的情况。

采用控制图分析胶膜厚度的起伏变化情况时，一般从一片晶片上的中间以及上下左右共5个位置测试5个胶膜厚度数据，作为控制图中的一批数据，采用均值-标准偏差控制图或者均值-极差控制图分析膜厚度的变化是否处于统计受控状态。显然，由于这5个胶膜厚度数据是同一片晶片上的数据，而同一片晶片上的胶膜是同时生成的。尽管该片晶片上的胶膜厚度不可能完全相等，而是服从一定的分布（一般为正态分布），但是如果该晶片胶膜厚度偏大，则这5个数据同时偏大。因此，就一般情况而言，如果控制图上同一批数据是同时生成的，例如上述半导体器件生产中的胶膜厚度，以及电镀工艺中的镀层厚度等，均具有嵌套特点。

另一方面，若干片晶片之间属于连续加工过程，由于对于大多数连续生产过程或已实现数据自动采集的过程都存在自相关性，因此，从总体考虑，每片晶片上的均值μd又存在自相关的特点。

由此可见，对于逐片批加工的过程（如：半导体贴胶工序）一般都既具有嵌套性又具有自相关性的特点，本文称具有这类特点的过程为“嵌套自相关过程”。关于该过程的质量控制，由于完全违背了独立同分布的假设，采用常规休哈特控制图或者嵌套控制图都有可能导致错误的结论，需要开发一种新的控制图解决该类过程的质量控制问题。

2 常规休哈特控制图与嵌套控制图比较

其中B3和B4为与样本含量n有关的常数，其值可从许多质量手册中查到。

则常规均值控制图的控制限为：

如果第i组样本服从均值为(μd)i、标准偏差为σd的正态分布，其中(μd)i之间不全相等；由各样本均值组成的随机变量{(μd)i}又服从另一个均值为μw、标准偏差为σw的正态分布，即“一阶嵌套过程”。其中，Xi称为嵌套随机变量，而不同批次的Xi构成的矢量｛Xi｝(i=1,2,…)称为一阶嵌套随机矢量，简称嵌套随机矢量。

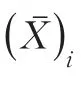
上述为一阶嵌套分布的控制模型，对于二阶嵌套等更复杂的情况，也可推得类似的数学模型。

式中Sw为每个嵌套随机变量均值的标准方差σw的估计值。

则一阶嵌套过程的所有测量值的样本总体标准偏差为

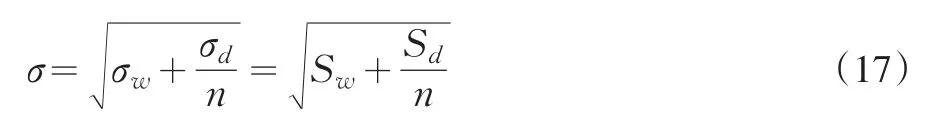
则嵌套过程的均值控制图的控制限为：

按照数理统计的原理，样本标准偏差组成的数列一般都是独立的，故样本数据相互独立情况下的嵌套过程的标准偏差控制图与常规标准偏差控制图一样。

3 嵌套自相关数据的控制图设计

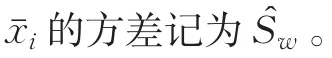
当每批测量值的均值之间存在自相关时，此时均值的方差发生变化，为：

比较式（22）和式（18），显然批均值自相关嵌套控制图的控制限小于嵌套控制图的控制限，原因是当过程存在自相关性时，均值会发生漂移，方差的计算应根据均值的漂移进行动态的计算，而动态的均值更接近局部数据测量值，使得方差减小，可以用自相关函数值对均值的方差的影响来表达。

4 实例分析

以半导体晶片涂胶工序为例，从某晶圆生产线上连续加工的25个晶片上各抽取5个数据，数据见表1。

表1 具有“嵌套”和“批均值自相关”特点的工艺参数数据（例）

（1）常规均值-标准偏差控制图的建立（不考虑“嵌套”和“批均值自相关”的情况）。

利用SPSS软件，画出该实例数据的常规均值-标准偏差控制图，见图1。

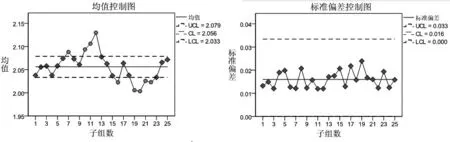
图1 常规均值-标准偏差控制图

均值控制图上均出现了多个数据点严重超出控制限的情况，而标准偏差控制图完全处于受控状态。对照表1可见，该组数据的特点是，同一批5个数据来自于同一晶片，片内分散性很小，因此每批的5个数据差别很小，即每批的标准偏差很小。而这组数据中不同批次之间数据分散性相对较大，即各批次之间平均值差别较大。

由于每批的标准偏差很小，根据式（6），由各批标准偏差的平均值0.016计算的均值控制图上下控制限分别为2.079和2.033，范围很窄，只有0.046。但是各组之间平均值的分散性较大，这就导致均值控制图上多个数据点严重偏离控制限。

（2）自相关性分析。

利用SPSS软件，画出批均值的自相关函数和偏相关函数，如图2所示，可见批均值之间存在自相关性，一阶自相关系数为0.702。

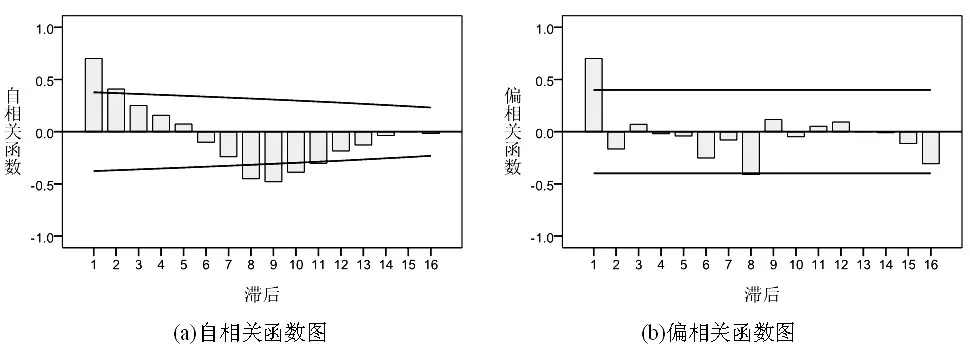
图2 批均值的自相关性分析

（3）嵌套控制图的建立（只考虑“嵌套”的情况）。

在样本数据相互独立的前提下，嵌套过程的标准偏差控制图与常规标准偏差控制图一样。根据式（18），嵌套过程的均值控制图的控制限为：

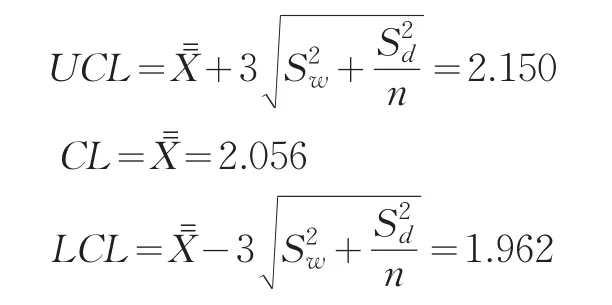
图3是利用上面计算结果绘制的控制图。由于考虑了过程的嵌套性，均值控制图上下控制限分别为2.150和1.962，控制图范围达到0.188，远远大于常规控制图的控制范围，均值控制图上未出现数据点超出控制限的情况。但是该嵌套控制图没有考虑过程存在批均值自相关的情况，由批均值的趋势图可以看出前12个数据属于渐进式均值漂移的情况，在第12个数据点远远高于所有测量值的均值2.056，属于失控点。因此，该控制图存在漏报警。

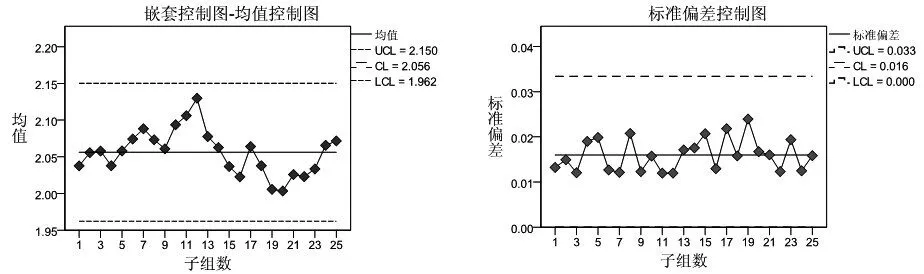
图3 嵌套控制图

（4）嵌套自相关控制图的建立（同时考虑“嵌套”和“批均值自相关”的情况）。

当嵌套过程存在自相关时，若仍使用常规嵌套控制图方法进行估算，往往导致控制限设置错误从而对质量的波动不能作出正确判断，可能导致漏报警。因此，为了提高控制图对特殊性原因的检测能力，当过程自相关时设计控制图，必须考虑过程的自相关结构。利用第3节提出的方法，存在批均值自相关的嵌套控制图（即嵌套自相关控制图）的控制限的计算结果为：

图4是利用上面计算结果绘制的控制图。该控制图由于同时考虑过程存在的嵌套性和批均值自相关性，控制图的控制限分别为2.111和2.002，控制图范围为0.109，小于常规嵌套控制图。嵌套自相关控制图显示第12个数据点偏离控制图，表明过程失控，由表1可以看出，该组数据远远大于其他各组数据，说明过程出现了异常情况。

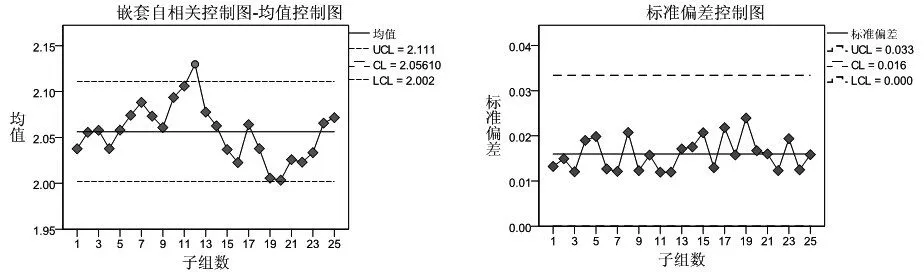
图4 嵌套自相关控制图

综上所述，当过程存在嵌套性和批均值自相关性时，采用常规休哈特控制图，由于控制范围较窄会出现大量误报警；采用嵌套控制图，由于控制范围较大容易出现漏报警；采用嵌套自相关控制图，相比常规控制图和嵌套控制图具有更高的检测能力，能够可靠的检测出过程的失控点。

5 结论

对于一些连续逐片批加工的生产过程，如：半导体晶圆生产、电镀工艺等，工艺参数数据往往存在“嵌套”和“批均值自相关”的特性，简称该类过程为“嵌套自相关过程”。本文引入自协方差函数和自相关函数，修正了传统嵌套控制图的控制界限，提出了一种嵌套自相关过程质量控制的新方法，即嵌套自相关控制图。以半导体晶片涂胶工序为例，对工艺数据的常规休哈特控制图、常规嵌套控制图和嵌套自相关控制图进行了比较分析，结果表明：存在嵌套性和自相关性的情况下，若继续采用常规休哈特控制图，则容易虚发警报；采用常规嵌套控制图，则容易漏报警；本文提出的嵌套自相关控制图具有更高的检测能力。因此，对于在生产过程中的嵌套自相关数据，建议使用嵌套自相关控制图来代替常规控制图。未来将进一步探讨自相关函数值对嵌套自相关控制图的影响，以及其它新的质量控制方法及其在实际生产中的应用。

[1]贾新章,李京苑.统计过程控制与评价——Cpk、SPC和PPM技术[M].北京：电子工业出版社,2004.

[2]高彩云.嵌套控制图在微波件腔体生产中的应用[J].电子质量,2008,(12).

[3]Vasilopoulos A V,Stamboulis A P.Modification of Chart Limits in the Presence of Data Correlation[J].Journal of Quality Technology,1978,10(l).

[4]Alwan L C，Roberts H V.Time-series Modeling for Statistical Process Control[J].Journal of Business and Economic Statistics,1988,6(1).

[5]Wardell D G,Moskowitz H,Plantz R D.Control Charts in Presence of Data Correlation[J].Management Science,1992,(38).

[6]Runger G C,Willemain T R.Model-based and Model-free Control of Autocorrelated Processes[J].Journal of Quality Technology,1995,(27).

[7]Jiang wei,Tsui K L.A New SPC Monitoring Method：The ARMA Chart[J].Technometrics,2000,42(4).