自适应样本量调整中Fisher合并P值法和传统检验法的模拟比较

王素珍,孟维静,吕军城,石福艳,夏结来

0 引言

样本量调整是临床试验自适应设计的一个热点问题，样本量调整的方法有很多，目前关注最多的是两阶段自适应设计的样本量调整。而在两阶段样本量调整中，又包括根据第一阶段的合并方差S21进行样本量调整、根据第一阶段的组间差值进行调整以及同时根据S21和进行调整等，本文主要研究根据S21和进行样本量调整时数据的分析方法。

第一阶段完成后，在盲态或揭盲状态下进行期中分析[1]，利用新得到的组间差值来代替最初设计的有临床意义的差值δ、新得到的合并方差代替原计划的方差重新计算样本量，受到很多统计学家的推崇[2-6]，本研究采用两阶段设计方法设计一安慰剂对照的临床试验，在揭盲状态下对样本量进行调整，借助蒙特-卡罗（Monte Carlo）计算机模拟方法[7]，采用SAS软件[8]模拟样本量调整中的两个阶段。第一阶段结束后估算组间差值以及近似方差并据此重新计算样本量，完成第二阶段的试验模拟，第二阶段结束后采用合并P值法分析全部数据，并与传统检验方法相比较，以探讨合并P值法对样本量调整后Ⅰ型错误和检验效能的影响，为两阶段设计在临床试验中的应用提供参考依据。

1 方法及设计

1.1 揭盲状态下利用δ和调整样本量的方法

假定有一研究某降压药疗效的安慰剂对照Ⅲ期临床试验，具有A，B两个处理组，分别接受治疗药物A和B，主要终点指标是仰卧舒张压SDBP（Supine diastolic blood pressure，单位mmHG）。现采用两阶段自适应设计方法设计该试验，即在试验进行中调整样本量[9～11]，同时观察药物疗效。由常识知A，B两个处理组的疗效均服从正态分布，根据先前的试验，预先估计处理组和安慰剂组的共同方差为，两组之间有临床有意义的处理差别为δ。由此可以计算在Ⅰ型错误概率α、检验效能1-β下试验所需的样本量N。初始方案中的第一阶段每组样本量为n1，即从总样本中取出一部分n1作为第一阶段样本进行试验，试验完成后在揭盲状态下计算组间差值δ以及合并方差

，据此重新计算整个试验的样本量Nrecalc，然后进行第二阶段的试验，第二阶段的样本量为重计算所得样本量减去第一阶段的样本量，即n=Nrecalc-n1。

1.2 模拟设计

由前面的假定已知A，B两个处理组的组间差值δ，共同的方差，现假定药物组A和安慰剂组B对应的主要疗效分别具有均值ux、uy，则模拟过程如下：应用SAS随机数函数rannor分别产生均值ux方差和均值uy方差的两组随机数各n1个，作为第一阶段的样本量。此处的为第一阶段的方差，此值可设置与相等或略有不等。第一阶段完成后，利用2n1个样本做期中分析，计算A，B两个处理组的组间差值以及合并方差，根据和重新计算样本量，模拟产生第二个阶段的数据。对上述两个阶段分别进行方差分析和合并P值法进行检验，其中方差分析法是对两个阶段的合并数据进行检验，而合并P值法则是对两个阶段分别做方差分析，然后将两个阶段得到的P值合并。不断改变n1的值，重复上述模拟试验。在既定的参数设置下，程序每循环一次对一个样本量为N的样本完成一次两阶段模拟，也即对一个样本量为n1的样本完成一次第一阶段模拟，两组的组间差为0时计算Ⅰ型错误，为某一固定值时计算检验效能对每一个既定的两阶段过程循环10000次计算Ⅰ型错误，5000次循环计算检验效能。n1从5开始，每次增加5个，直到达到总样本量的80%。

2 结果

根据前面假定的研究某降压药临床试验例子产生模拟数据，先前研究得到的两组SDBP与基线相比平均舒张压下降的差值δ=3，方差=64，在Ⅰ型错误α=0.05时，获得1-β=0.9的检验效能所需的最初样本量为151例，简单起见取150例，即N=150，从中取一定比例的样本量n1=πN模拟第一阶段试验。第一阶段的组间效应即是两组SDBP与基线相比平均舒张压下降值的差值，此值与最初设定值相同，即3mmHG，第一阶段的方差与最初设置的不同，设为=92=81，据此产生第一阶段模拟数据。由模拟数据计算出组间均值差的估计值，以及第一阶段的合并方差，并根据1j和重新估算样本量，进行第二阶段的试验，第二阶段的模拟数据根据和产生。在 δ1j=0时，计算Ⅰ型错误，而在δ1j=3mmHG计算检验效能。在不断变化第一阶段样本量的条件下，比较方差分析法和合并P值法的Ⅰ型错误和检验效能。对每一个既定的样本量完成10000次循环计算Ⅰ型错误，5000次循环计算检验效能。所得结果如表1和表2所示。其中N_ips为第一阶段样本量，MeanNr和MedNr分别为10000或5000次重计算的样本量的均值和中位数，MeanN2和MedN2分别为第二阶段样本量的均值和中位数。表1中最右侧的两列分别对应方差分析法和合并P值法的Ⅰ型错误；表2中最右侧的两列则分别对应两种方法的检验效能。

由表1可以看出，调整后样本量的均值比最初预设的样本量要大。这是因为在模拟Ⅰ型错误时，假定两组间的均值差为0，此时在第一阶段完成后，计算得到的两组间差值会很小，因此重计算的样本量较大。当第一阶段样本量较小时，比如小于70（约为最初设计样本量的一半左右）时，方差分析法的Ⅰ型错误明显高于合并P值法，而第一阶段样本量高于70时，方差分析法的Ⅰ型错误逐渐减小，没有出现大于名义检验水准0.05的情况；而合并P值法的Ⅰ型错误却还出现大于0.05的情况。这似乎告诉我们，当采用IPS方差及观测到的组间差值进行样本量调整时，如果第一阶段的样本量较小，比如小于最初计划样本量的一半时，则应采用合并P值法对两阶段数据分别分析；而在第一阶段样本量大于计划样本量的一半时，可采用方差分析分析两阶段的合并数据。然而，从表2的检验效能比较中却发现，在样本量较小时，合并P值法的检验效能远低于方差分析法的检验效能，比如当第一阶段样本量为20时，方差分析法的效能为0.828，但合并P值法的检验效能却只有0.682，离预期的检验效能相差太远，因此我们只根据Ⅰ型错误就断定IPS样本量较小时应采用合并P值法来分析数据是不合理的。

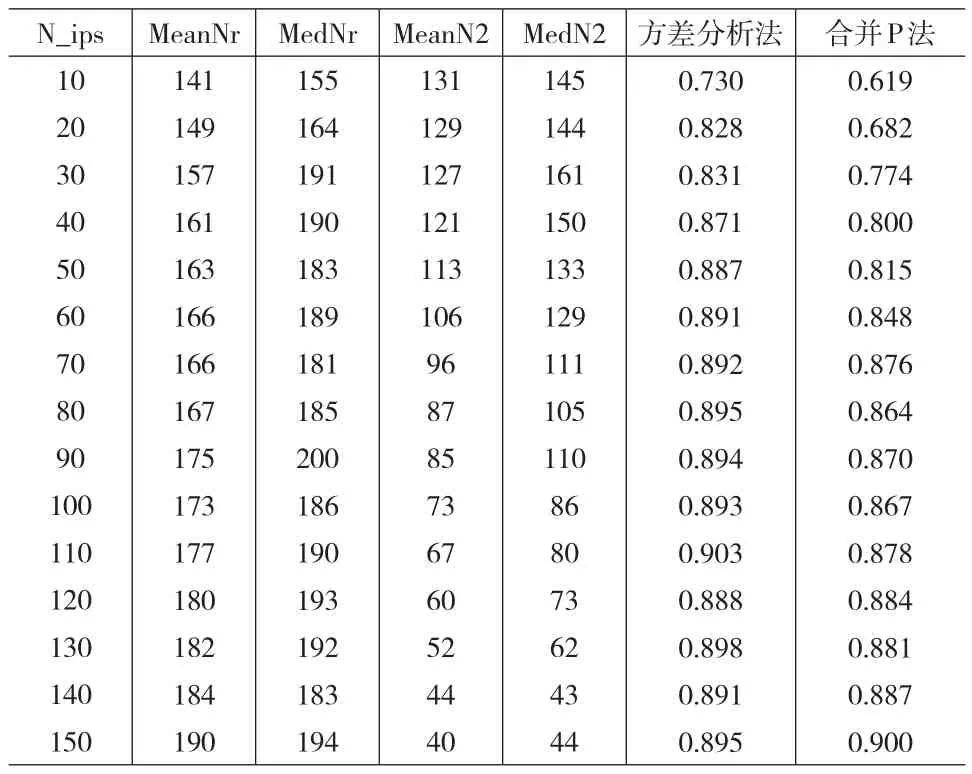
表2 方差分析法和合并P值法在不同IPS样本量时的检验效能

3 讨论

自适应样本量调整中，Ⅰ型错误的膨胀一直为人们所关注[1，4]。综合本文中两种方法的Ⅰ型错误和检验效能，可以得出这样的结论：当采用第一阶段方差及观测到的组间差值进行样本量调整时，第一阶段的样本量不能小于计划样本量的1/3，在此为50例，若小于计划样本量的1/3，则无论采用传统的统计方法还是采用合并P值法，都很难在控制Ⅰ型错误和保证检验效能之间达成较好的平衡，因为此时如果采用方差分析法，则Ⅰ型错误过大；采用合并P值法，Ⅰ型错误略有增大，但是检验效能过低。当第一阶段样本量大于计划样本量的1/3而小于计划样本量的一半时，应选择合并P值法，此时虽然检验效能有所降低，但是可保证Ⅰ型错误不增大。而当第一阶段样本量超过计划样本量的一半时，则应采用方差分析法分析两个阶段的合并数据，此时既有较高的效能，又能防止Ⅰ型错误的增大。

样本量调整中不增大Ⅰ型错误，不仅与药物审批要求[17]相一致，而且节约了成本，保证了试验的可行性。在样本量调整过程中，合理的选择检验方法，是保证试验成功的关键因素之一。本文给出了不同样本量时检验方法的选择途径。另外，在模拟中还有两个随机数，即调整后的样本量Nrecalc和第二阶段的样本量n2，这两个值同样对Ⅰ型错误和检验效能有影响。由于样本的随机性，有时根据第一阶段数据得出的很小，而很大，使得重计算的样本量非常大；有时得出的很大，而很小，重计算的样本量就会很小。当重计算的样本量很小时，可以按照Birkett和Day[13]的规限制则，取重计算的样本量不小于第一阶段的样本量；但是当重计算的样本量很大时，按照Birkett和Day的规则，应该取重计算样本量和第一阶段样本量中的较大者，这会使得重计算的样本量相当大，有的甚至到了上万例，使得第二阶段的临床试验变得根本不现实。这无论对临床试验的申办方还是研究者，都是难以接受的。重计算样本量的目的就是为了节约成本，在用最少样本的情况下得出最准确可靠的结论。如果重计算的样本量大于原计划样本量的4倍，应即视之为异常值。为了防止异常值的出现，应该对第一阶段设计有效或无效停止的边界，比如，可以按照检验效能做出规定：如果条件效能至少为60%的话，则增加样本量，否则的话，就宣布无效停止；也可以按照第一阶段检验所得的P值做出规定，当P值小于或大于某一临界值时，宣布试验有效或无效，及时停止试验，这样可以避免因出现异常大的样本量调整值而导致试验无法进行。

[1] Zucker D.M.,Wittes J.T.,Schabenberger O.et.al.Internal Pilot Stud⁃ies II:Comparison of Various Qrocedures[J].Statistics in Medicine,1999,(18).

[2] Bauer P,Kohne K.Evaluation of Experiments with Adaptive Interim Snalyses[J].Correction in Biometrics,1996,(52).

[3] Proschan MA,Hunsberger SA.Designed Extension of Studies Based on Conditional Power[J].Biometrics,1995,(51).

[4] Kieser M,Friede T.Simple Procedures for Blinded Sample Size Ad⁃justment that do not Sffect the TypeⅠ Error Rate[J].Statistics in Med⁃icine,2003,(22).

[5] Lan KKG,Wittes J.The B-value:A Tool for Monitoring Data[J].Bio⁃metrics,1988,(44).

[6] Liu Q,Chi Gyh.On Sample Size and Inference for Two-stage Adap⁃tive Designs[J].Biometrics,2001,(57).

[7] Sheldon M.Ross,Simulation.(3th Edition)[J].Printed in China by POSTS&TELECOM Press,2006.

[8] SAS Institute Inc.SAS/STAT User's Guide Version 8.2[CP/CD].North Carolina,2006.

[9] Werner Brannath,Peter Bauer,Martin Posch.On the Efficiency of Adaptive Designs for Flexible Interim Decisions in Clinical Trials[J].Journal of Statistical Planning and Inference,2006,(136).

[10] Zhu Chunhua,Chen Guijing.Some Optimal Adaptive Designs in Clinical Trials[J].Chinese Journal of Applied Probability and Statis⁃tics,2005,(21).

[11] Wittes J,Brittain E.The Role of Internal Pilot Studies in Increasing the Efficiency of Clinical Trials[J].Statistics in Medicine,1990,(9).