二阶亥姆霍兹共鸣器的隔声特性*

赵 准，孔 鹏，邓 科

(吉首大学物理与机电工程学院，湖南 吉首 416000)

随着工业化的大肆发展，空气噪声控制成为重要的民生问题.近年来，声学人工结构逐渐成为吸隔声降噪领域研究的热点.声学人工结构一般是指由人工设计具有天然材料不具备的特殊物理性质的复合材料.常见的声学人工结构大都由尺寸远小于波长的结构单元组成，通过精确的几何参数设计调节，声学人工结构能够实现对声波的吸收、阻隔和过滤等新奇效果[1-5].

随着声学人工结构的蓬勃发展，腔式声学超材料成为了近些年的研究热点.其主要是通过对亥姆霍兹共鸣器结构进行改良，进而达到摒弃腔体尺寸对共振频率的限制.2014年，Cai等[6]率先提出了一种将亥姆霍兹共鸣器背腔加长并进行盘绕的设计概念，实现了对400 Hz附近的低频声波完美吸收的效果；虽然，这种背腔盘绕结构使腔式声学超材料突破了1/4波长的限制，实现了较低频降噪.但是，其共振频率单一的缺陷限制了腔式声学超材料的进一步发展.2017年，Chen等[7]将2段不等径的细长共振腔串联拼接，并盘绕成圆盘状.两段细长腔分别在各自的共振频率达到了完美吸收.通过调节两段长腔的内径和长度，使2个共振峰之间距离适中，便可实现拓宽吸收带宽的效果；对共振腔结构的改良除了可以实现低频和宽频降噪，还可以达到对多频段噪声的控制效果.2019年，刘志恩等[8]提出了一种新型并排式多腔亥姆霍兹共振消声器结构.将多个不同频率的共振腔并排式布置在管道同一截面，能做到并排式共振腔传递损失性能互不干涉，且能有效地消除多个不同频率处的噪声值.综上所述，改良亥姆霍兹共鸣器对噪声控制的应用有着重要的研究意义[9-15].笔者运用传递矩阵和有限元仿真相结合的研究方法，设计了一种二阶亥姆霍兹共鸣器，该结构设计简单，调节方便，通过对几何参数的调节能有效的对两个噪声频段进行隔声降噪.

1 传递矩阵法建立数值理论模型

图1(a)是二阶亥姆霍兹共鸣器结构，该结构由内插短管1、空腔1、内插短管2、空腔2这4个主要部分组成.内插短管及腔的单个传递矩阵形式实质上是与主管流道(波导管)的传递矩阵相一致的，该体系中所使用的等效波数公式(1)和等效阻抗公式(2)如下：

(1)

(2)

图1 二阶谐振腔单元的二维结构与等效阻抗模型示意Fig. 1 Schematic Diagram of Two-Dimensional Structure and Equivalent Impedance Model of Second-Order Resonator Element

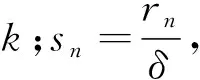
本研究将二阶亥姆霍兹共鸣器结构的每个细致的组成部分都等效成一层超薄的阻抗边界，等效模型如图1(b)所示.黄色层代表波导管与内插管1前端管口部分的阻抗边界层，用不连续性传递矩阵MΔl2表示；红色层代表整个内插管1部分的阻抗边界层，用传递矩阵Mneck表示；蓝色层代表内插管1后端管口与空腔1部分的阻抗边界层，用不连续传递矩阵MΔl1表示；绿色代表整个空腔1部分的阻抗边界层，用传递矩阵Mcavity表示；蓝色代表空腔1与内插管2前端管口部分的阻抗边界层，用不连续传递矩阵MΔl1表示；红色代表整个内插管2部分的阻抗边界层，用传递矩阵Mneck表示；蓝色代表内插管2后端管口与空腔2部分的阻抗边界层，用不连续传递矩阵MΔl1表示；绿色代表整个空腔2部分的阻抗边界层，用传递矩阵Mcavity表示；黑色代表刚性末端，用Rigid表示.

通过等效模型图推导出管口与末端的声压、质点速度关系为

(3)

其中：Bneck为内插管传递矩阵，

(4)

Bcavity为空腔的传递矩阵，

(5)

BΔl1为内插管口与空腔的不连续传递矩阵，

(6)

BΔl2为内插管口与波导主管的不连续传递矩阵，

(7)

因此，可以得到二阶共振腔单元的系统等效阻抗

(8)

上述公式中，Δl1为内插管口与空腔的修正长度：

(9)

Δl2为内插管口与波导主管的修正长度：

(10)

其中，rk为内插管半径，rmain为波导主管等效半径，rc为空腔等效半径.通过传递矩阵得到的二阶谐振腔单元系统的总的传递矩阵M可以求得系统的声强透射系数T如公式(11)以及传递损失(隔声量)TL如公式(12).

(11)

TL=-10log10T.

(12)

笔者运用传递矩阵法，分层推导出二阶亥姆霍兹共鸣器的系统阻抗，并建立用于隔声降噪的数值理论模型.将数值理论模型编程在Matlab软件中，便可通过大量的结构参数进行数值计算分析二阶亥姆霍兹共鸣器的隔声性能.

2 二阶亥姆霍兹共鸣器的隔声仿真

将数值理论模型编程在Matlab软件中，通过参数调节设计了2组用于主管道侧腔隔声的二阶亥姆霍兹共鸣器参数模型.为了验证2组参数模型的可行性，进行了Matlab数值计算与Comsol Multiphysics有限元仿真计算相结合的验证工作.本研究验证的2组二阶亥姆霍兹共鸣器的几何参数列于表1.图2(a)表示的是二阶亥姆霍兹共鸣器在主管流道的侧方工作的三维仿真示意图，数值计算与仿真计算的传递损失(隔声量)结果的对比数据如图2(b)所示.

表1 2组二阶谐振腔单元的几何参数

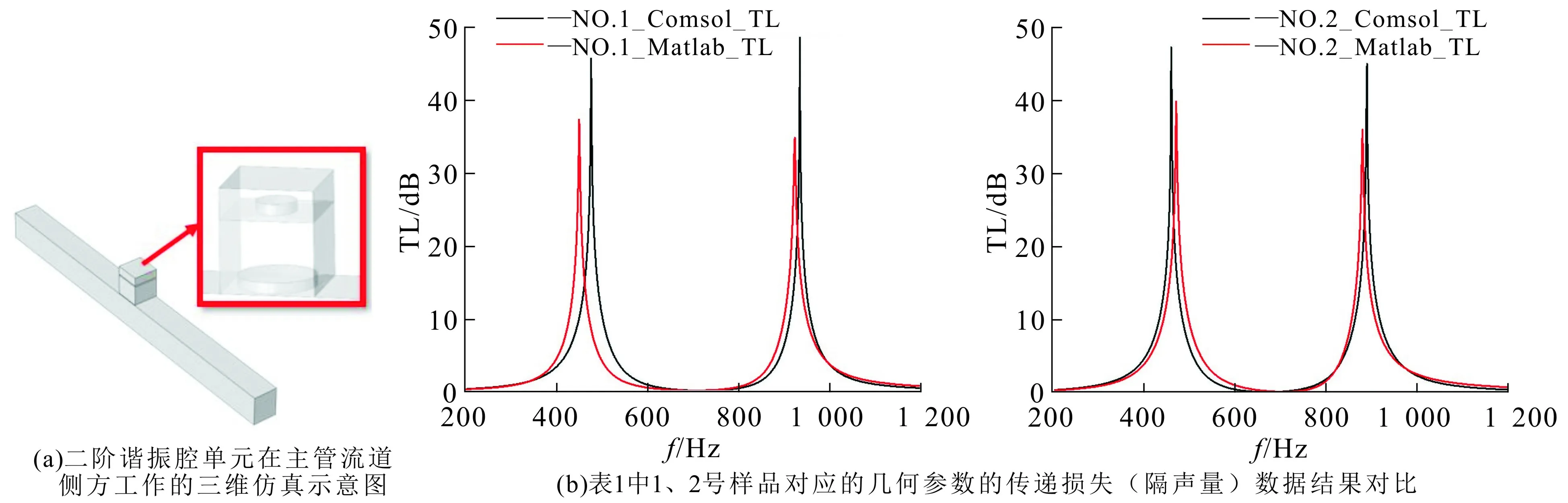
图2 二阶谐振腔单元工作示意图与2组结构参数的数据结果Fig. 2 Schematic Diagram of the Second Order Resonator Cell and the Results of Two Groups of Structures

从图2(b)中可以看到，二阶亥姆霍兹共鸣器存在两个传递损失(隔声量)峰值.以Comsol Multiphysics有限元仿真计算结果为对比数据，1号样品的隔声工作频率在470 Hz和920 Hz，2号样品的隔声工作频率在450 Hz和864 Hz，且隔声量在两个工作频率处均可达到较高的隔声效果(40 dB左右).从图2(b)结果表明，1号和2号样品的数值计算结果与仿真计算结果匹配度较高，仅有微小偏差，且最大并不会超过20 Hz.仿真结果较好地验证了二阶亥姆霍兹共鸣器隔声的优异性能和理论模型的精确性，对二阶亥姆霍兹共鸣器的隔声降噪理论有着重要的研究意义.

3 总结

本文在传统亥姆霍兹共鸣器的结构基础上，改良设计出一种基于高阶共振的亥姆霍兹共鸣器结构.通过传递矩阵法将二阶亥姆霍兹共鸣器结构进行分层推导，建立了较为精准的数值理论模型.将数值理论模型编程在Matlab软件中，通过参数调节设计了两组用于主管道侧腔隔声的参数模型.并对两组模型进行Comsol Multiphysics有限元仿真计算的验证，传递损失(隔声量)结果匹配度较高，且隔声量在工作频率处均可达到40 dB左右的高性能隔声降噪.可见，二阶亥姆霍兹共鸣器结构在多频段噪声控制工程中有广泛的应用前景.