磷烯-硼碳二磷异质结电子输运性质的掺杂调控*

吴 丹，廖文虎，林丽娥，罗淑珍，程小丽

(吉首大学物理与机电工程学院，湖南 吉首 416000)

磷烯由1层排列在六角形皱褶晶格中的磷原子构成，现已经被人们从块体黑磷结构中成功分离出来[1-3].磷烯因拥有独特的能带结构而具有十分有趣的特性，包括有效质量的高度各向异性和可以通过应变调节的电子特性，从而电子可以一系列跃迁为直接半导体、间接半导体、半金属和金属[4-5].此外，磷烯具有极高的电子迁移率[2]和随层数变化的透射带隙[6]，从块体到单层带隙由0.30 eV增加至约2.00 eV.这些特性使得磷烯在纳米电子学和光电子学领域中有重要的应用[1，7-9].

目前，基于二维材料的异质结构提供了新的构建器件的方法，而将不同性能的二维材料缝合或堆叠在一起有望为设计具有特定性质的新材料提供机会.对石墨烯-氢化硼氮单层异质结[10-11]、过渡族金属化合物半导体-过渡族金属化合物异质结[12-13]和过渡族金属化合物-黑磷异质结[14-15]等的研究表明，这些异质结不但表现出组分材料本身优异的物理特性，还克服了的单一材料的不足.磷烯具有优异的物理性质和广泛的调制范围，将它与其他二维层状材料进行堆叠能够形成范德华尔斯异质结，研究显示，基于磷烯的此类异质结构在晶体管设计方面得到了成功应用[16-18].

硼碳二磷(BC2P)是一种类似于石墨烯完全平坦的六角蜂窝结构的稳定的硼碳磷化合物单层[19]，它是间接带隙半导体，能隙为1.41 eV.磷烯与BC2P的晶格常数非常接近，将两者通过一定的方式堆叠，能够形成稳定的范德华尔斯异质结.因此，笔者拟利用磷烯与BC2P构建扶手椅边缘和锯齿边缘范德华尔斯异质结电子输运器件，并利用密度泛函理论与非平衡格林函数相结合的第一性原理计算方法，研究有限偏压下2种边缘形貌异质结的电子输运性质，以及N型电子/P型空穴掺杂对2种边缘形貌异质结电子输运性质的影响.

1 结构模型与计算理论

1.1 磷烯-硼碳二磷范德瓦尔斯异质结器件的结构模型

沿扶手椅边缘磷烯的晶格常数为0.437 nm，BC2P的晶格常数为0.487 nm；沿锯齿边缘磷烯的晶格常数为0.331 nm，BC2P的晶格常数为0.282 nm.沿扶手椅边缘用2个磷烯元胞匹配沿锯齿边缘3个BC2P元胞，沿锯齿边缘用3个磷烯元胞匹配沿扶手椅边缘2个BC2P元胞，从而构建了磷烯-硼碳二磷(P-BC2P)超胞.P-BC2P超胞原子结构的俯视、正视和侧视图如图1所示.为了方便起见，规定超胞中磷烯的扶手椅边缘/锯齿边缘形貌为超胞的边缘形貌.

图1 P-BC2P超胞的原子结构Fig. 1 Atomic Structure of P-BC2P Supercell

将P-BC2P超胞沿x或z方向拓展4个单位作为中心散射区，沿垂直磷烯平面使用应力压缩为原始厚度70%的磷烯作为左、右电极(左、右电极为半无限长，其中的一部分作为缓冲层放入中心散射区)，这样搭建的扶手椅边缘和锯齿边缘P-BC2P范德瓦尔斯异质结器件的结构如图2所示.采用虚拟晶体近似方法[20-22]对异质结中的磷烯层进行N型电子和P型空穴掺杂，掺杂浓度为0.001～0.01 e/atom.为了屏蔽相互作用，除了输运方向外，其他2个方向均添加1.5 nm的真空层.

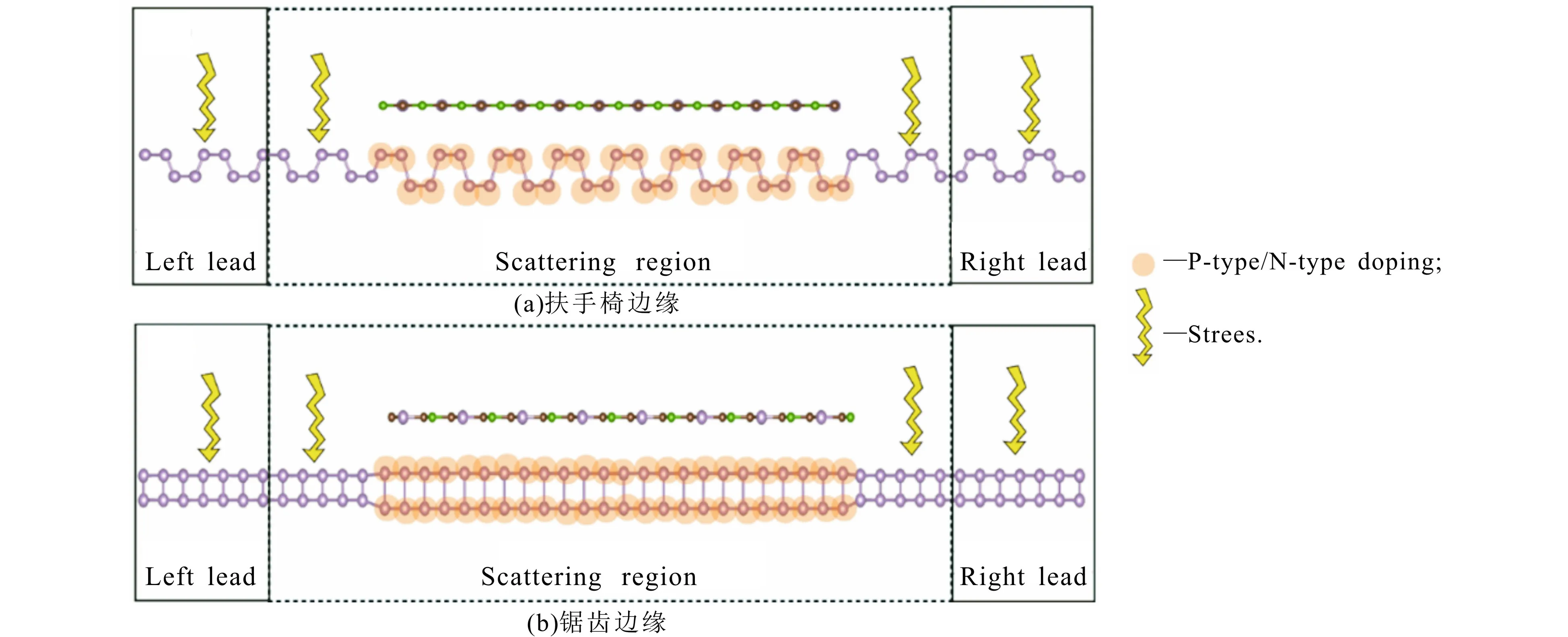
图2 P-BC2P异质结器件的结构Fig. 2 P-BC2P Device

1.2 磷烯-硼碳二磷范德瓦尔斯异质结电子输运性质的计算理论

采用密度泛函理论结合非平衡格林函数[23]的第一性原理计算方法，借助Nanodcal量子输运软件包[24]，对P-BC2P器件的电子输运性质进行数值计算.研究过程中选用双ζ极化原子轨道基组扩展物理量，费米温度为100 K，能量截断半径为80 Hartree，交换关联形貌使用GGA_PBE96，采用Pulay算法进行迭代更新，混合率为0.01.电极和中心区自洽循环的K点取值分别为1×1×100，1×1×10，哈密顿量和密度矩阵的收敛标准为10-5.

电极α中的自旋非极化电流可用如下Landauer-Büttiker公式进行计算：

(1)

其中fα()是在电极α中电子的费米-狄拉克分布函数，2倍因子来自自旋简并度.

2 数值模拟结果与讨论

2.1 有限偏压下磷烯-硼碳二磷范德瓦尔斯异质结的电流和电导

现来讨论有限偏压对P-BC2P异质结的电流和电导的影响.为了更好地理解P-BC2P异质结的物理特性，选取同样宽度的本征磷烯纳米带(P)作为对照.此外，考虑到超胞中BC2P六角环上原子位置的不对称性，同时研究反向偏压作用P-BC2P范德瓦尔斯异质结(P-BC2P*)的影响.图3示出了-1～1 V偏压范围内扶手椅边缘/锯齿边缘P、P-BC2P和P-BC2P*异质结的电流-电压曲线，图4示出了-1～1 V偏压范围内扶手椅边缘/锯齿边缘P、P-BC2P和P-BC2P*异质结的电导-电压曲线.

图3 -1～1 V偏压范围内P、P-BC2P和P-BC2P*异质结的电流-电压曲线Fig. 3 Current-Voltage Curves of Phosphorene Nanoribbons, P-BC2P and P-BC2P*Heterojunctions in the Range of -1～1 V Bias Voltage

图4 -1～1 V偏压范围内P、P-BC2P和P-BC2P*异质结的电导-电压曲线Fig. 4 Conductance-Voltage Curves of Phosphorene Nanoribbons, P-BC2P and P-BC2P*Heterojunctions in the Range of -1～1 V Bias Voltage

由图3可见：(1)扶手椅边缘和锯齿边缘P-BC2P异质结的电流在偏压绝对值为0～0.2 V范围内几乎线性增大，随着偏压绝对值的进一步增大，电流振荡上升.(2)改变偏压方向对2种边缘形貌P-BC2P异质结的电流几乎没有影响，P-BC2P与P-BC2P*的电流仅在较大偏压下定量上稍有不同.(3)扶手椅边缘P-BC2P异质结的电流的增长快于同样宽度扶手椅边缘P的，最大电流达到扶手椅边缘P的2倍；锯齿边缘P-BC2P异质结的电流的增长慢于同样宽度锯齿边缘P的，最大电流不足锯齿边缘P的1/2.

由图4可见：(1)在-1～1 V偏压范围内，扶手椅边缘和锯齿边缘P-BC2P异质结均呈现有负微分电阻现象.(2)同偏压下，2种边缘形貌的P-BC2P异质结与P-BC2P*异质结的电导非常接近.(3)同偏压下，扶手椅边缘P-BC2P异质结的电导几乎均高于扶手椅边缘P的，而锯齿边缘P-BC2P异质结的电导几乎均低于锯齿边缘P的.

2.2 有限偏压下磷烯-硼碳二磷范德瓦尔斯异质结的电子透射谱

图5示出了0～±1 V偏压下扶手椅边缘和锯齿边缘P-BC2P异质结的电子透射谱.图中，垂直能量轴的2条(0 V偏压下为1条)虚线给出与能量范围对应的偏压窗口，偏压窗口内电子透射系数的积分面积用S表示.由Landauer-Büttiker公式可知，电流和电导变化的微观机理可以通过电子透射谱的变化直观地反映.也就是，通过偏压窗口内的电子透射系数的积分面积的变化直观地反映电流的变化，积分面积越大，电流越大；通过费米能级附近的电子透射系数的分布直观地反映电导的变化，透射能隙越小，电导越大.

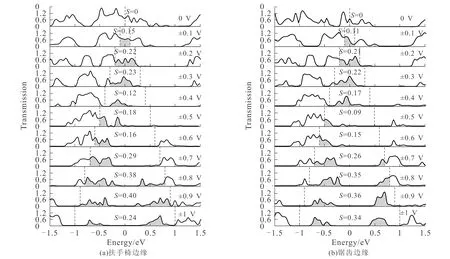
图5 0～±1 V偏压下P-BC2P异质结的电子透射谱Fig. 5 Electron Transmission Spectrum of P-BC2P Heterojunction Under 0～±1 V Bias

对比图3～5可知，0～±1 V偏压下，2种边缘形貌P-BC2P异质结电子透射系数的积分面积的增减与电流的增减一一对应，透射能隙的增减与电导的增减一一对应.这说明，2种边缘形貌P-BC2P异质结的电流和电导的变化得到电子透射谱的有力印证.

2.3 N型电子/P型空穴掺杂调控磷烯-硼碳二磷范德瓦尔斯异质结的电导

图6示出了掺杂浓度0.001～0.01 e/atom范围内N型电子/P型空穴掺杂对扶手椅边缘和锯齿边缘P-BC2P异质结的电导的调控结果.未掺杂时，扶手椅边缘和锯齿边缘P-BC2P异质结的电导分别为0.75G0，0.28G0.

图6 掺杂浓度0.001～0.01 e/atom范围内P-BC2P异质结的电导-掺杂浓度曲线Fig. 6 Conductance-Doping Concentration Curve of P-BC2 Pheterojunction in the Range of 0.001～0.01 e/atom Doping Concentration

由图6(a)可见：掺杂浓度0.001～0.01 e/atom范围内，P型空穴使扶手椅边缘P-BC2P异质结的电导最多升至0.90G0和降至0.60G0，相比未掺杂时分别增加和减少20%；N型电子掺杂使扶手椅边缘P-BC2P异质结的电导最多降至0.40G0，相比未掺杂时减少46.7%.

由图6(b)可见：掺杂浓度0.001～0.01 e/atom范围内，P型空穴掺杂使锯齿边缘P-BC2P异质结的电导最多升至0.83G0，相比未掺杂时增加196%；N型电子掺杂使锯齿边缘P-BC2P异质结的电导最多升至0.74G0，相比未掺杂时增加164%.

3 结论

利用密度泛函理论与非平衡格林函数相结合的第一性原理计算方法，研究了有限偏压下扶手椅边缘和锯齿边缘P-BC2P范德瓦尔斯异质结的电子输运性质，以及N型电子/P型空穴掺杂对2种边缘形貌异质结电子输运性质的影响.有限偏压下的电流-电压曲线和电导-电压曲线显示，2种边缘形貌P-BC2P范德瓦尔斯异质结均呈现非线性变化和负微分电阻效应.扶手椅边缘P-BC2P异质结的电流增长快于扶手椅边缘磷烯纳米带，负微分电阻效应更强；锯齿边缘P-BC2P异质结的电流增长慢于锯齿边缘磷烯纳米带，负微分电阻效应更弱.掺杂浓度0.001～0.01 e/atom范围内的N型电子/P型空穴掺杂的电导-掺杂浓度曲线显示，2种边缘形貌异质结的电导呈现不同的调控结果.相比未掺杂，扶手椅边缘P-BC2P异质结的电导在P型空穴掺杂时最多增加和最多减少均为20%，在N型电子掺杂时最多减少46.7%；锯齿边缘P-BC2P异质结的电导在P型空穴掺杂时最多增加196%，在N型电子掺杂时最多增加164%.研究结果可为基于磷烯异质结的电子器件设计提供参考.