数学眼光的内涵及培养

胡晋宾 (江苏第二师范学院数学系 210013)

刘洪璐 (江苏省南京师范大学附中数学组 210003)

1 问题提出

当下数学课改中倡导“三会”理念，“提升学生的数学素养，引导学生会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界”[1]．从某种意义上来说，“三会”就是数学教育的终极目标，也是高中阶段核心素养的本质．相对于“三会”中的数学思维和数学语言来说，数学眼光(和“数学的眼光”等价)虽然经常被使用，但是它相对“年轻”，在实际教学中存在很多歧义和误读．比如，在数学教育中常见术语有数学知识、技能、能力、思维(思想)、文化等，数学眼光的内涵和这些似乎都有联系，但是具体怎样去界定则未见系统论述．如果含混地说数学眼光本质上是核心素养的综合体现，那么就很容易加重概念的模糊性．如果把“三会”当做一种终极的上位培养目标，那么会在教学转化时存在一定的落地困难．由此可见，数学眼光该怎样去界定和剖析乃至培养，是个亟待研究的问题．

2 内涵思辨

2.1 眼光的语义

眼光有以下几种语义：第一，名词，视线的意思．例如：大家的眼光都集中到他身上．第二，观察鉴别事物的能力，眼力．例如：这辆车挑得好，你真有眼光．第三，指观点．例如：老眼光，用发展的眼光看问题．[2]实际上，一般语言中所说的眼光，比如说这人很有眼光，意思是见解认识独到深邃，考虑问题长远非凡．

2.2 内涵厘清

数学眼光的本质是什么呢？通常所说的数学眼光，当然不是生理意义上的眼光．比如欧拉在失明以后还能做高深的数学研究，显然不能说此时他没有了数学眼光．从本质上来说，相对于没有学习过数学的人或数学不好的人来说，具有数学眼光的人拥有略胜一筹或者与众不同的数学能力(核心素养)或观念意识．

数学眼光的特点是什么呢？不妨先比较后回答．既然有数学眼光，那么也就有物理眼光、美术眼光、语文眼光、体育眼光等．如果说物理眼光考察的是物质和变化、美术眼光关注的是造型和色彩、语文眼光聚焦的是情感和表达、体育眼光考量的是体质和技能的话，那么从根本上来说，数学眼光就是生发于数学学科特性视角的一种思考，关切的是“数学是数量关系和空间形式”内涵，彰显的是“思想材料的形式化抽象”特点．比如纸盒子与三视图问题中，并非就是去打开和折叠纸盒子，而是要最终在大脑中建立表象并进行空间想象．再如，著名的哥尼斯堡七桥问题，不是去关心河流的长宽、水质的清浊、桥梁的色泽、材料的软硬等，而仅仅考虑岛屿和陆地之间借助穿河而过的桥梁之间的结构关系，将桥抽象为线段，将岛屿和陆地抽象为点(空间形式)，最终转化为一笔画问题加以解决．正因如此，数学课程标准中强调的“数学地思考”就是“在大脑中”思考和解决问题，而无须实际地操作．[3](即使有“实实在在的”实际操作，那也仅仅是“辅助的思维工具”.)换句话说，这就是数学和其他学科的差异所在，也就是数学眼光的要害所系．

数学眼光体现了什么数学核心素养呢？史宁中指出，数学教育的“终极培养目标都可以描述为：会用数学眼光观察现实世界，会用数学思维思考现实世界，会用数学语言表达现实世界”[4]．数学眼光从本质上来说是核心素养的体现．我们不妨用斯托利亚尔和弗赖登塔尔的话语来解读数学眼光．斯托利亚尔认为，“数学教学应该是数学活动的教学”，并且指出数学活动可以分为3个阶段：“第一，经验材料的数学组织化；第二，数学材料的逻辑组织化；第三，数学理论的应用．”显然，上述3个方面大致对应着3个基本思想，即抽象、推理和建模．换句话说，我们可以对“经验材料”作些拓展，数学的思考对象不一定就是物质层面的经验材料，也有可能是精神层面的经验材料，数学抽象即是在相关事物中提炼出更加抽象化和一般性的数学内涵．因此，数学眼光主要涉及经验材料的数学组织化阶段．在弗赖登塔尔数学化理论中，数学化有水平和垂直数学化之分，其中水平数学化和现实有关联，数学眼光主要就是发生在水平数学化阶段．现在有些论文中把从现实中抽象出数学问题，直至最后用数学方法加以解决的整个过程，都当作数学眼光，这种把垂直数学化的相关工作也泛化为数学眼光的做法是不合适的．因为如果这样泛化，那么就没必要提及另外的“两会”即数学思维和数学语言了．

如果用“四能”(发现、提出、分析和解决问题)来解释数学眼光的话，数学眼光主要对应发现和提出数学问题这两个阶段．对于数学活动来说，数学眼光最为重要，主要体现在：从相关的问题中发现数学内涵，或者有了数学内涵之后怎样去想到现实案例．至于接下来该怎样去解决问题、怎样去表达推广，这些就是“三会”中的另外“两会”，即用数学思维去思考和用数学语言去表达的事情了，已经不再是数学眼光的“地盘”了．正因如此，史宁中等认为，数学眼光主要表现为三大基本思想中的数学抽象，主要涉及数学抽象和直观想象两种核心素养．而数学思维主要表现为推理，数学语言主要表现为模型．它们三者分别呼应数学的高度抽象、逻辑严谨和应用广泛的特点．上述关系可以用图1来表示．

图1 “三会”、基本思想与数学特点对应关系

综上，数学眼光是数学学科核心素养的具体表现和数学教学的最终培养目标之一．数学眼光主要就是在现实与数学之间进行的思维切换，也即：立足知识储备，关涉活动经验，借助数学抽象和直观想象，从现实案例“看到”数学内涵，从数学内涵“想到”现实案例．在数学学习和实践中，当我们看到相关的现实情境后，具有数学眼光的人会不由自主地抽象出相关数学知识，而一旦提到某个数学知识，也会自动想象到现实中的具体案例．

2.3 维度划分

基于上述定义，数学眼光的理论框架如图2所示．第一，现实维度(或者说情境与问题维度)：生活现实、数学现实、其他学科现实(或者熟悉的情境、关联的情境、综合的情境)．(水平可以理解为从低到高共3级.)第二，素养维度：数学抽象，直观想象．从现实案例“看到”数学内涵主要是数学抽象，从数学内涵“想到”现实案例主要是直观想象．水平划分可以对照课标中的刻画，如表1和 表2所示．[1]课标中对数学抽象和直观想象的水平划分是按照情境与问题、知识与技能、思维与表达、交流与反思4个角度来阐述的，实际上如前所述，思维与表达、交流与反思涉及“三会”中的后“两会”(数学思维和数学语言)，和数学眼光不相吻合，故而不予考虑．第三，数学维度(或者说知识与技能维度)：数与代数，图形与几何，统计与概率．(综合与实践领域是综合运用前述3种领域知识，故而不作独立维度.)

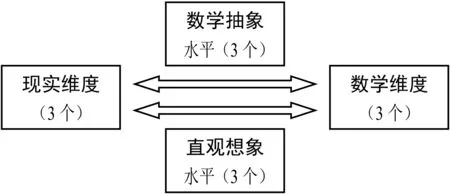
图2 “数学眼光”模型示意

3 机理探讨

3.1 发生机制

数学眼光是怎么运作的，将直接涉及怎样培养和落实．

首先，数学眼光和知识技能有关．没有知识作支撑，是不宜奢谈眼光的，知识越多越有利于产生数学眼光．比如，张景中院士的《数学家的眼光》[5]中的案例，阅读之后让人叹为观止．数学家的眼光和他们自身渊博的知识基础、高超的数学能力以及丰富的研究经历有关系．显然，他们的数学眼光比普通人更加独到、深刻、犀利、敏锐、多元．他们往往会看到别人看不到的数学关系，抽象出较为深刻的数学内涵，直观想象到更多的现实案例等．当然，我们也可以这样理解，接受过好的数学教育的人相较于没有接受过好的数学教育的人，数学眼光也会有如此差异．

其次，数学眼光和活动经验有关，这一点与教师平时的教学有关．虽然当前的教材中有很多情境和生活的案例，但是要让学生养成数学眼光，还需要个体日积月累的实践磨砺．显然，具有数学眼光或者数学眼光厉害的人，不一定应试能力就很强．

表1 数学抽象水平划分

表2 直观想象水平划分

再次，数学眼光和联系实际的意识与能力有关系，最为重要的是抽象能力以及直观想象能力．就数学抽象而言，按照郑毓信的分类，主要有等置抽象(也叫等价抽象，比如从数量中抽象出数)、理想化抽象(比如在生活中抽象出点、线、面概念，以及哥尼斯堡七桥问题的欧拉解决等)、强弱抽象和存在性抽象(比如抽象出虚数i及无穷远点)等种类．[6]实际上，限于学生的水平，日常中主要是前3种抽象．就直观想象而言，需要强调的是，虽然数学强调逻辑严谨，但是数学学习和研究中直观和想象无处不在，我们无论如何强调都不为过．

3.2 实例剖析

以下就亲身经历的2个案例来加以说明．

(1)集合案例

我们在编写集合教材时安排了以下“阅读题”作为练习，以期培养学生的数学眼光：“一位渔民非常喜欢数学，但他怎么也想不明白集合的意义．于是，他请教数学家：‘尊敬的先生，请你告诉我，集合是什么？’集合是不定义的概念，数学家很难回答那位渔民．有一天，他来到渔民的船上，看到渔民撒下鱼网，轻轻一拉，许多鱼虾在网中跳动．数学家非常激动，高兴地告诉渔民：‘这就是集合！’”[7]显然，水里的鱼是全集，打进渔网的鱼和漏网的鱼正好是集合的互补关系．

打鱼的现实和其中的关系刺激了个体的思考，从中抽象概括出数学集合知识．更进一步，从中还可以“看出”著名的等周定理．当然，一旦提到集合的概念，我们还会想到现实中的更多案例．

(2)圆锥曲线案例

图3 壁灯与圆锥曲线

在许多地方都有类似如图3所示的灯具．晚间点亮的时候，就会发现墙壁上有曲线的影子．它看起来像是抛物线，果真如此吗？实际上，圆锥曲线可被看作是用一个平面从不同角度去截取圆锥后得到的截线：当平面经过圆锥面的顶点时，可以得到等腰三角形；当平面与圆锥面的轴垂直时，可以得到一个圆；当平面与圆锥的轴夹角不同时，可以分别得到椭圆、双曲线和抛物线．图3中的灯泡就相当于点光源，发出光之后被灯罩阻挡，形成一个类似圆锥的光柱．而这时墙壁就相当于截平面，显然这个截平面平行于圆锥轴线，所以它是双曲线．

反思上述过程可以发现：首先，个体需要具备相应的数学知识和经验．其次，相关场景激活了大脑中的原有知识，个体产生了数学抽象、直观想象、联想类比等思维活动．再次，个体把相应现象和数学知识做了模式识别和关联匹配，或者利用数学知识去搜寻现实中的模型并得到了圆满的解释，突然领悟到数学原来在这里．

4 培养策略

4.1 经历知识生成，发展概括抽象

数学知识的学与教中既有过程也有结果．这种过程主要就是弗赖登塔尔所说的数学化．数学眼光中，主要是和现实相关的水平数学化(而非垂直数学化)．数学眼光的培养要多关注应用，密切联系，经历过程，从实际和应用中发展学生的概括抽象能力，帮助学生把握知识本质；尽量围绕数学的内涵和本质，结合不同现实(生活现实、学科现实和数学现实)展开日常的教学．当然，我们也必须指出，要防止以下的几种误区：数学课中的去数学化，没有聚焦数学主旨；数学课的庸俗化，缺少数学味道；数学的泛情境化，即每节课都必须要情境或生活化．

4.2 发展直观想象，强调关联转换

数学学习与研究中不仅有基于模型的直观和表象把握，而且有汪洋恣肆的想象和联想．正因如此，伏尔泰说数学之神阿基米德比荷马更有想象力．数学发展历史告诉我们，它是鲜活丰富的，是激情四射的．不能因为数学的严谨性而窒息了数学中的想象．想象和数学不是截然对立的，甚至文学和数学也有相通和互补的地方．比如，历史上就有多个数学出身的文学家，如罗素、索尔仁尼琴、库切获得过诺贝尔文学奖．再如，有很多数学家的文学修养很高，比如华罗庚、苏步青、丘成桐、张景中等．总之，“科学和艺术在山底下分手，在山顶上会合”．为了培养学生的数学眼光，教师在备课的时候应该基于学生的现实，设计相应的环节，加强不同知识之间或者知识与生活实践之间的联系；多关注数学文化，能够在生活常识和数学知识之间、在数学知识的不同学科应用和前后之间切换(比如数形结合、前后呼应)．

4.3 积累活动经验，注重数学应用

现实教学中我们往往功利地短视于应试，而忽视数学素养的积累和沉淀．数学学习和教学不仅仅是让学生掌握一些静态死板的知识，或熟练一些推算技能，或掌握一些应试技巧，还需积累一些经典案例，因为这远胜一打抽象理论．因此教师应该在日常教学中，经常和学生一起戴着“数学眼镜”，用数学眼光来审视多重现实(生活、数学和其他学科)，融入不同的知识学习；挖掘整理一些经典案例，让学生逐步积累相应活动经验，关注数学综合应用与反思，炼就数学眼光的“火眼金睛”．此外，教师还可以让学生多阅读数学科普读物，以便开阔眼界、砥砺眼光．