初高中数学的衔接重在思想方法的衔接*
孙居国 (江苏省南京师范大学附属中学 210003)
当前初高中数学衔接的问题,广大学生和教师都非常重视,新教材在内容的安排上也进行了调整,作了一些补充和拓展,以使学生能尽快适应高中数学的学习.但是对“衔接”问题,不少师生还存在一些误区,认为只要补充一些知识,例如对一些高中数学有影响的运算进行加强,包括乘法公式、因式分解等,有的甚至提前学习高中数学内容,但对数学思想方法方面的衔接还不够重视.为使学生能尽快适应高中数学的学习,本人认为关键是重视思想方法的衔接.
1 从图形直观转化为代数抽象
初中数学学习中几何的内容很多,特别是对一些较难的内容,借助于图形的直观性,可以符合初中学生的认知规律,取得较好的学习效果.有时在中考压轴题中,也是兼顾图形直观,例如南京市2020年中考数学压轴题:
名酒企业具有得天独厚的品牌优势,更受消费者信任。因此,我们要承担起责任,推动行业进行产品创新、品牌创新、服务创新,实现消费者价值担当、渠道价值担当和行业价值担当。
如图1,要在一条笔直的路l边上建一个燃气站,向l同侧的A,B两个城镇分别铺设燃气管道,试确定燃气站的位置,使铺设管道的路线最短.
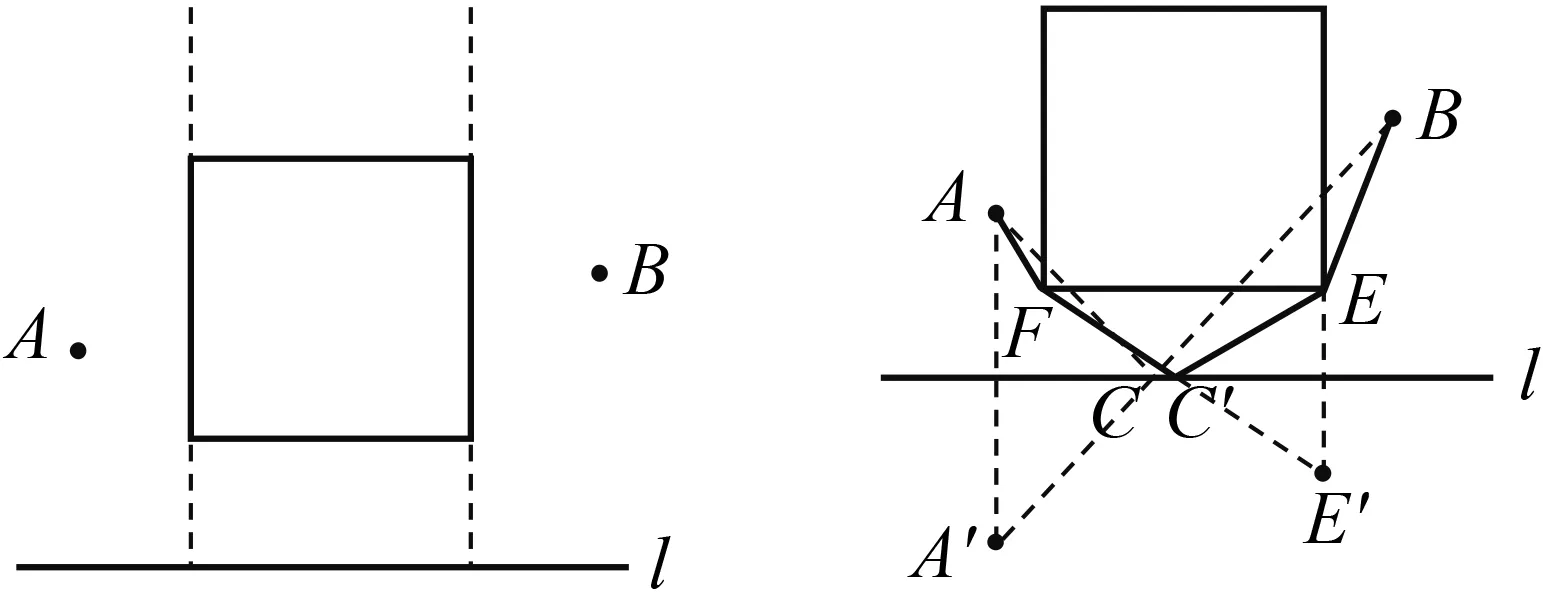
(1)如图2,作出点A关于l的对称点A′,直线A′B与直线l的交点C的位置即为所求,即在点C处建气站,所得线路ACB是最短的.为了证明点C的位置即为所求,不妨在直线l上另外取一点C′,连结AC′,BC′,证明AC+CB 图1 图2 (2)如果在A,B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域.请分别给出下列两种情形下的管道铺设方案(不需要说明理由). ① 生态保护区是正方形区域,位置如图3所示; ② 生态保护区是圆形区域,位置如图4所示. 南方公司2018年8月宣布项目估计造价增加超过20亿美元,因此项目业主在9月底就该项目的未来进行投票表决。 图3 图4 解析 (1)连结A′C′.因为点A,A′关于直线对称,所以CA=CA′,故AC+CB=A′C+CB=A′B.同理AC′+C′B=A′C′+C′B.因为A′B 图5 图6 此题如果作为对数学习的引例,则是比较好的,能引起学生学习的兴趣,使学生懂得证明的功能不仅是从已有结果获得一个新的结论,而且能帮助学生形成对数学知识的理解和洞察;让学生懂得欣赏经验的作用和思维中的猜测作用.若作为一个题目给初中学生讲解,则会影响他们对数学的全面理解,甚至会出现科学性的错误.教师在教学中要认真区分已经证明和没有证明(或因受中学数学限制,暂时不能证明)的事实. 在这一前提下还需再分类讨论(图8-图10). 图7 图8 图9 图10 而原题中只是一种情形,说明高中与初中对学生的要求不一样,初中相对直观简单,而高中则对理性思维的要求更高,思考问题应更加全面且深刻. 吕剧故乡文化产业项目少、规模小、社会文化消费水平不高。省、市、区电视台虽然播出一些吕剧,但存在资料匮乏、播出时间和栏目不固定等现象。民间文化队伍未形成较大演艺阵容,文化演出特别是吕剧庄户剧团、民间演艺公司习惯于传统性经营,吕剧文化产业发展和市场化运作水平较低。目前,东营市吕剧博物馆、雪莲大剧院等一批文化场馆设施的建设有助于吕剧文化的宣传推介和振兴发展。必须抓住机遇,通过“产学研销”四位一体的市场经济运作模式的建立和文化旅游市场的培植等手段,坚定不移地走产业化发展之路。 题1求函数f(x)=x2-2ax-3(-1≤x≤1)的最小值. 图11 例如,函数单调性的处理:如何利用函数解析式f(x)=x2描述“随着x的增大,相应的f(x)随着减小”“随着x的增大,相应的f(x)随着增大”? 巴乌是音乐教学中常用的乐器,它音域较窄,简单易学,在教学过程中,老师先让学生熟悉巴乌的十个音节,知道是低音,1 2 3 4 5 6是中音,并让学生在巴乌上找出各个音对应的位置,然后音乐老师再进行示范演奏,让学生模仿自己吹奏单音,从低音到中音进行逐一体验式练习,培养学生的音高概念和识谱能力,正所谓“冰冻三尺非一日之寒”,再有天赋的学生也要通过反复操练才能把握好音调的高低和演奏的节奏。小学生乐器的学习不能过于死板,老师要以组织游戏的方式进行乐器的教学,寓教于乐是促进学生学习积极性的重要手段,同时也让他们感受到学习巴乌演奏的乐趣。 由解法可知,本视频的受众应是初中学生,因为解法是初中数学的方法,估计其目的是培养指数运算的技巧,提高变形的能力.题目短小精悍,有一定的深度,且是一题多解,可以激发学生的学习兴趣.对初中学生来说还有一定的难度,但对于高中学生而言,就是比较简单的题. 但仔细思考,此解法中存在着问题.在题目中,没有给出a,b的范围.查阅初中教材,规定指数一定是正整数次幂的运算,也就是说在初中数学中,若出现ba,则a是正整数.而5a=2b=10,对于初中学生而言,是一个矛盾的式子,因为不存在这样的整数a,b,使得5a=2b=10成立. 规定锚节点和传感器节点均采用如图1所示的三方向线圈天线,图中线圈Ck(k=1,2,3)之间互相正交且圆心重合,d表示节点S与锚节点之间的距离,xyz为以锚节点为原点建立的局部坐标系,坐标轴分别对齐对应的线圈的几何轴线。采用电流源对3个发送线圈依次激励,则在节点S处分别产生磁场作用。 到了高中以后,要求从图形直观转化为代数抽象.学生不但要知道怎么做,还要知道为什么这样做,把每一个数学问题想清楚、想明白,形成思考的习惯,逐步适应高中数学学习的要求. 方法1中出现由式子10ab=10a+b,得ab=a+b也存在问题,说不清楚,这要用到函数的单调性. 如今,这种生活陶艺不再像高端的艺术品,慢慢走近平民百姓的生活,已经变成了我们生活的一种时尚。与古人相比,当今的生产制造水平大大提升。现代化的加工机械和设备,如今的陶器成型可以直接在拉坯机上操作,现在丰富多彩的釉料、颜料可以让我们装饰陶器作品。科学技术的不断提升,不但能给我们生活带来更多的便利,更加能在艺术创作中给我们先决条件,这也是当今陶艺作品不断蓬勃发展的动力所在。 因此,要解决此问题,显然学生的知识储备不足.很显然,这是高中教材中的问题,用高中数学中的解法如下: 二、中职学生自主学习能力现状分析通过对本校学生的调查,能主动学习的只有26%。不难发现,中职学生自主学习能力低,状况令人堪忧。原因分析如下: 用此方法解此题时,学生要用到大量的知识,首先要用到指数从整数推广到分数、有理数、实数的过程,还要用到指数的概念和性质以及对数的概念和性质,本人认为把这样的对数题下放给初中学生做是不妥的,对学生的数学学习不利.要从这种“不求甚解”转化到“步步有依据”,从操作技巧转化到思想方法,可以借助于此题引入,从而将整数指数幂推广,或引进对数的概念. 学生常常出现如下的问题:忽视概念、公式、定理成立的条件,只追求结果的正确、方法的奇异,把最常规的思想方法给摒弃了;对细节不能追求到位,粗枝大叶,舍本求末,不求甚解.现在有很多做法在推波助澜, 有的高中自主招生时,出的数学试题有不少的内容是高中数学内容,有个别学生得到较高的分数,显然是提前学习了高中数学知识或参加过竞赛辅导,尽管暂时获得了好成绩,但到了高中,随着学习的深入,优势则会越来越不明显,甚至被其他同学反超.有的学生初三暑假就将高一数学内容学完,实际上是提前学.随意拓宽知识,加重学生的学习负担,这种做法可能只符合极少数学生,对大部分学生来说是不利的. 说明在高中教学要求中,这种做法还不够,需要分下列情况讨论:第一要说清楚,点A的位置在正方形区域的左侧,点B的位置在正方形区域的右侧(图7). (2)①如图5,在点C处建燃气站,铺设管道的最短线路是ACDB(其中D是正方形的顶点). 企业通过PLM系统实施和应用过程中的标准化工作,实现产品数据的统一管理,简便快捷的电子签审,方便的产品文档齐套审查,文档版本的有效控制,资源共享,质量管理体系与PLM系统的有机结合,工作流程的标准和统一等。企业标准化工作与PLM系统之间是相互依存的共同体。标准化工作是PLM系统建立和实施的基础,并始终贯穿于每一个环节;PLM系统的成功实施又将推动企业标准化工作的开展和进步,将标准化要求尽可能地嵌入设计、管理、生产等工作流程,使得标准化工作的重心可以从日常烦琐的标准化审查转为制定各类“规则”,充分发挥PLM系统的各项功能。 若作为复数的引入,则很好,若作为题目让学生解,就不妥了.因为对学生而言,方法不确定,结论不确定,因此也就不存在严谨性了.如果有学生说答案不存在,你说这样的回答对不对?学生怎么也想不通两个数的平方和为负数! 整个数学是一个科学体系,数学教学要符合学生的认知规律和数学发生、发展的特征,要有连续性、逻辑性,循序渐进.若打破知识的结构,将会对学生的长远发展不利.而上述解法显然是记方法、代模式、不求甚解的表现. 本例幕上肿块型血管母细胞瘤因组织结构致其磁共振成像信号特征存在特殊性,为今后提高血管母细胞瘤影像诊断的准确性积累经验,存在一定的临床研究参考价值。 清楚的前提、清楚的推理,才能得出清楚的结论.数学中的命题,对就是对,错就是错,不存在丝毫的含糊.我们说,数学是易学的,因为它是清楚的,只要大家按照数学规则,按部就班地学,循序渐进地想,绝对可以学懂;我们又说,数学是难学的,也因为它是清楚的,如果有人不是按照数学规则去学去想,总是把“想当然”的东西强加给数学,在没有学会加法的时候就想学习乘法,那就要处处碰壁,学不下去了. 运算能力是数学的重要能力,初中运算能力主要是指能够根据法则和运算律正确地进行运算的能力.而高中数学运算指在明确运算对象的基础上,依据运算法则解决数学问题的素养,主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果.数学运算是解决数学问题的基本手段,是演绎推理,是计算机解决问题的基础. 在初中数学运算中,运算通常是目标,依据法则和运算律,侧重于计算,抽象度低(数与式),是静态的运算.例如求函数y=x2-x-3的最小值,这类题在初中经常出现,直接配方或代公式即可,即依据的法则和运算律正确就行了. 再看下面两个高中常见的问题: 其次,照片成为超文本之后,一张完整的照片能充当节点,成为一张超照片,是正在发展的对话的一个不明确的、形象化的、未解说的、诱人的数据段,只要读者愿意,他可以被引至其他照片、其他媒介、其他观念。[1]69当它们接入网络环境里,摄影被讨论和被重估: 题2求函数f(x)=x2- 2ax-3(-a+ 1≤x≤2a+1且a>0)的最小值. 在高中数学运算中,运算通常是手段,选择法则和运算律,侧重于运算,抽象度高(数与式、集合运算、向量运算),是动态的运算.随着数学中新概念的不断出现,促使运算对象不断增加,并逐步抽象化. 思维型学习疑难也称组织型学习疑难,它是在信息的组织时出现的异常情况而产生的学习疑难.美国学者安东尼·格里高根据知觉的具体与抽象,规则的次序与随机将人类的思维分成了四种:具体而有序的思维、抽象而有序的思维、具体而随机的思维、抽象而随机的思维[25].这四种思维类型并无好坏之分,但它们之间的思维形式有所不同[26].不同的思维形式在一方面表现出一些优势的同时,往往在另一方面会表现出劣势,以致于出现一些思维障碍,从而产生思维型学习疑难. 再看下面一高中问题:已知关于x的函数y=f(x),y=g(x)和h(x)=kx+b(k,b∈R)在区间D上恒有f(x)≥h(x)≥g(x).若f(x)=x2+2x,g(x)=-x2+2x,D=(-∞,+∞),求h(x)的表达式. 由于涉及的知识点多,对学生的思维能力、运算能力、应变能力有很高的要求.该题层次分明,内涵丰富,值得品味.具体分析如下. 一级配电系统保护开关由于和二级三级配电系统在设计中需要进行选择性设计,往往上一级保护开关选择具有三段式保护功能的短路器,而下一级保护开关选择具有两段式保护功能的断路器,这样的设计能将事故中停电范围缩小至故障回路中,提高了其他用户对用电要求的需要,也利于排查检修故障电器设备。 The comprehensive language is used in a tense system,and the usual class score is 40 points.In that the new teaching mode has a significant effect on the improvement of students'performance,have real validity. 这就要求进入高中后,在数学教学过程中,学生对数学概念的理解要清晰,基础知识、方法的掌握要精确到位,教师要强化知识间内在的联系,强调推理过程的严谨性,强调训练的有效性,特别是要突出不同数学语言间的统一性,文字语言、符号语言、图形语言相统一和协调.平时课堂教学中要注意学生的语言表达,使得数学思维和数学表述相一致.还要注意平时练习中有时虽然选择题、填空题的答案是正确的,但数学思维不一定正确,推理不一定严密,甚至可能是错误的,因此不能只满足于答案正确,还要借助于课堂的优势,强调为什么这样做,通过师生对话、生生交流来相互启发,使得解题的每一步精确到位,提升严谨的数学思维,积累精准的解题经验,形成规范的数学表述习惯,突出“四基”,强化“推理”. 从初中到高中,是数学学习的两个不同阶段,其中的数学概念、数学方法与数学思想既有区别又有联系.就像篮球训练,初级阶段是定点投篮、运球、防守等较为单一的要求;高级阶段中除了继续进行定点投篮、运球、防守等训练外,更要加强运动中投篮、有障碍的运球、有防守的投篮等,对体力、协调性、应变性、相互配合等要求更高.因此,为了实现初高中数学学习的无缝对接,不但要在知识、方法上对接,更要着重数学思想方法的衔接,加强兴趣培养,拓展数学视野,帮助学生尽快适应并喜欢高中数学的学习.在学习知识的过程中,还应注重能力的培养.在学习完每一章节后,帮助学生整理所学知识和方法,形成稳定和完善的知识结构,再适当补充一些重要的知识方法,提高学生的解题能力和数学思维水平,从而逐步形成数学的基本思想、基本方法和基本态度.
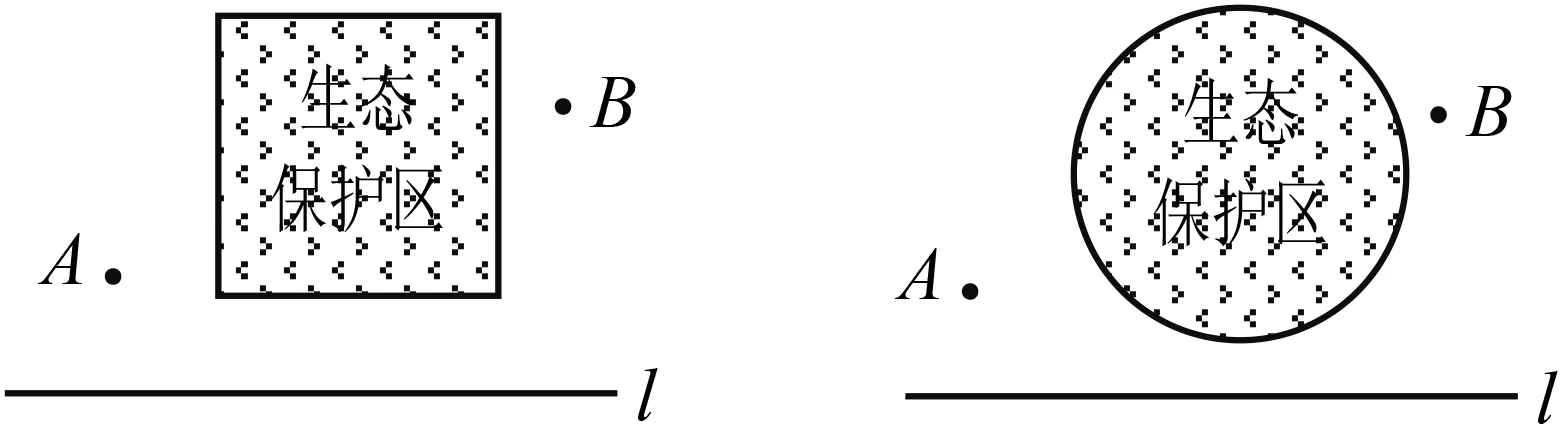
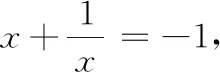



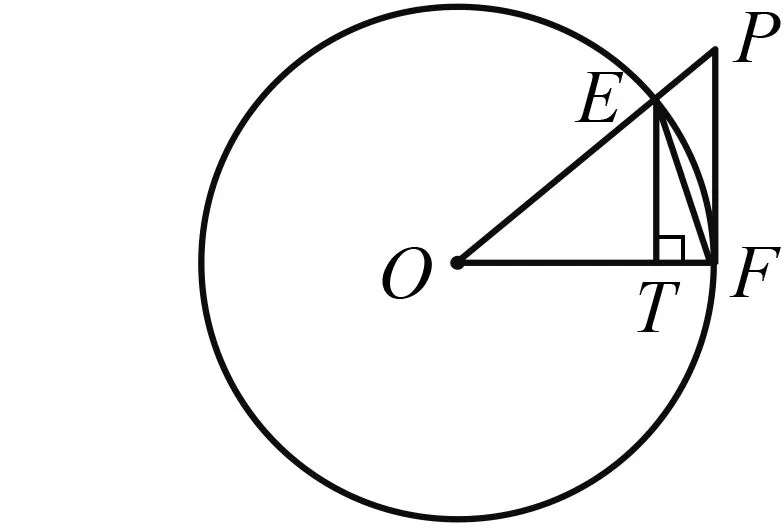



2 从操作技巧转化为精准推理


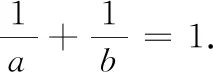
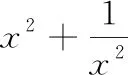

3 从静态计算转化为动态运算

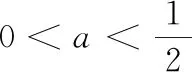
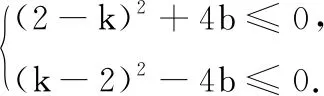

4 结束语

