数学教育实证研究科学化：思考与建议

蔡金法 (西南大学数学与统计学院 400715 美国特拉华大学数学系 19716)

徐冉冉 (西南大学数学与统计学院 400715)

姚一玲 (杭州师范大学教育学院 311121)

实证研究是一种基于事实和证据的研究，是教育学走向科学的必要途径[1-2]．实证主义哲学创始人孔德(Auguste Comte,1798—1857)认为，一切知识都必须建立在观察和实验的基础上，经验是一切知识的来源，经验范围以外的知识都是不可靠的[3]．纵观包括教育学在内的学术发展史，可以发现实证研究是提高社会科学研究科学化水平的重要保证[4]．在西方，实证研究已成为教育研究的主流，是学术交流和期刊论文的基本范式，也是美国制定教育政策的基本思维方式[5]．例如，国际顶尖数学教育期刊“Educational Studies in Mathematics”和“Journal for Research in Mathematics Education”(简称ESM 和JRME)迄今刊发的论文多为实证研究[6]．与之相比，中国教育实证研究才刚刚起步，实证研究论文不足论文总数的15%，大多数论文仍停留在主观性的思辨和应然性的畅想阶段[7-9]．因此，加强和改进教育实证研究，是中国教育研究的当务之急．

近年来，国内关于加强教育实证研究的呼声不断高涨．特别是2017年初，14所大学的教育科学学院、32家教育研究杂志以及全国教育科学规划办公室和光明日报教育研究中心在华东师范大学联合召开了“全国教育实证研究联席会议”，共商加快教育研究发展、提高教育研究质量之策，共同发布了《加强教育实证研究，促进研究范式转型的华东师大行动宣言》，推进和深化中国教育研究中的实证研究范式转型．尽管越来越多的教育研究者开始注重实证研究，并使实证研究逐渐成为中国教育研究的主流，但中国学者的研究成果极少见诸于国际公认的高水平教育期刊上[10-11]．比如，迄今为止，没有任何一位中国大陆学者在国际顶尖数学教育期刊JRME上公开发表过科研论文．此外，研究范式和研究方法不能很好地与国际接轨，也使得中国学者在国际研究舞台上很少能发出强而有力的声音[12]．

可见，我国的教育研究迫切需要加强对实证研究方法的运用，提高教育实证研究的科学化水平．因此，本文结合国际优秀实证研究案例，针对数学教育实证研究科学化提出几点思考与建议．以期有助于更多教育研究者规范实证研究的范式与方法，扩大研究问题和研究领域，提高教育研究成果质量，增强中国教育研究在国际上的地位与影响力．

所谓实证研究，一是要仔细选择问题，使研究的问题具有学术价值和实际意义；二是要了解该问题的研究情况，即别人已经做了什么，我能贡献什么；三是根据问题选择适当的方法(定性或定量)，借以切实地进行论证[13]．基于此，特从“数据说话与研究类型、数据说话与理论框架、数据说话与实践智慧、数据说话与原因分析以及非认知能力——实证研究的重要内容”5个方面进行简要介绍．

1 数据说话与研究类型

研究类型不同，所需要的数据也是不一样的．美国教育科学研究所(The Institute of Education Sciences)和美国国家科学基金会(National Science Foundation)两个机构出版的《教育研究与发展的共同准则》[14](Common Guidelines for Education Research and Development,2013)提出了6种类型的研究：基础研究(Foundational Research)、早期阶段或探索性研究(Early-Stage or Exploratory Research)、设计与开发研究(Design and Development)、效能研究(Efficacy Study)、有效性研究(Effectiveness Study)和大样本的推广研究(Scale-up Study)．该报告介绍了每种类型的研究大概需要用什么样的数据，为什么用这样的数据可以回答该类型的研究问题，以及什么样的数据是无法回答该类型的研究问题的．举例来说，对“基础研究”而言，如果用大量的调查进行研究是没办法说明它的研究问题的．例如，一项关于脑科学的“基本研究”通过对脑扫描的数据可以发现：以前认为大脑不可以改变，但现在的研究表明大脑可以在很短的时间内改变．即我们在学习新东西时，就是在我们大脑内建立联系．然而，该研究结果通过调查等其他方式是无法得到的．又如，对“有效性研究”而言，其目的是在常规实践条件下实施某个干预或策略，从而观察这些干预或策略所产生的影响．因此，简单做个访谈或调查也是无法揭示这些干预或策略的有效性．

研究问题是实证研究的开端，研究问题的类型决定了所需要的研究方法、数据类型及数据收集手段与分析方法等．如若不然，研究所得的结果将可能无法准确而深入地回答所研究的问题．用“两种不同研究方法对同一研究问题进行研究”的例子加以详细说明．例如，通过定量分析和定性分析两种方式收集数据，研究“学生对数学的情感是怎样的？”．

(1)定量分析：整体评分．在5个选项(1-5分进行赋分，依次代表非常负面、中等程度的负面、一般或态度不明朗、中等程度的正面、非常正面)中勾选出一个对数学的情感评价，收集相关数据，得出以下初步结果(图1)．

(2)定性分析：揭示学生所使用的比喻类型以及为什么？

a.编制研究工具

我们对你怎样思考和感知数学很有兴趣，请花一点时间思考下面的问题并写下你的真实感受．另外，所有这些问题并没有所谓正确或错误的回答．

①如果数学是一种食物，它可能是；因为．

②如果数学是一种颜色，它可能是；因为．

③如果数学是一种动物，它可能是；因为．

b.收集数据(学生回答)，并得到以下两类不同的结果．

一类是表明喜欢数学的例子：“数学像牛排，因为数学是一个面很广的学科．然而，牛排有的部分很硬很难啃．虽然整顿饭的最后感受还是满意的，但吃的过程挺费力的”；“蔬菜是对你有利的，就像数学对于日常的事物．生活中需要它．一些人喜欢它，而一些人不喜欢它，但健康的生活却离不了它”．一类是不喜欢数学的例子：“数学像蚊子，因为无论你试图怎样躲避它，它总会回来的．让我讨厌的是每天都要上数学课，无论你试图怎么逃避它，你总是不会得逞的”；“数学像口香糖，你嚼它并且用它来清新自己的口气，但嚼到最后它变得毫无价值而且一点营养和维生素也没有．学校里的数学能影响你的智力，但日后的生活却用 不上”．

通过对比两种不同研究工具对同一研究问题的调查结果发现：用定量分析作为研究工具进行调查，能够说明样本的总体情况，但无法揭示导致这一结果的具体原因；相反，用定性分析作为研究工具进行调查时，由于样本量的限制，或许无法得到总体趋势，但学生对数学的情感状态和导致结果的原因却可以更容易、更准确地描述．也就是说，在做一项研究时，首先要明确到底想要回答什么研究问题，然后用较多的时间去思考什么办法能够把这个现象测量出来，以至于可以深入地研究下去，从而让现象可以精准地被描述出来．换言之，实证研究首先以研究问题为主，研究问题确定了用什么样的数据和研究方法，方法、数据等皆是为回答研究问题而服务的，而不是数据的形式决定回答什么样的研究问题．换言之，用什么样的研究方法，是根据要回答什么样的研究问题，怎样才能更好地回答这个研究问题来确定的[15]．

2 数据说话与理论框架

数据需要理论框架来指引．当设计需要收集什么样的数据的时候，首先需要确定一个理论框架．同样地，在进行实证性研究数据的收集、分析和解读时，也需要借助理论框架来指导，而非让数据引导整个研究．举两个例子加以说明．

第一个例子：检验中美学生对平均数算法的概念性知识与程序性知识的理解[15]．

文献研究表明，学生对数学知识的理解包括概念性知识理解与程序性知识理解两个方面．在该理论的指导下，我们该如何了解学生的知识理解属于哪种类型呢？又该如何分析所收集的数据呢？

只有在具体了解学生数学知识理解类型的情况下，才能在课堂上有效帮助学生在这两方面的理解．用下面的例子加以说明，如何在理论指导下调查和分析学生对算术平均数的概念性和程序性理解．

1.在一次食品捐赠活动中，小张、小王、小李和小赵分别捐赠了一些罐头．其中小张11罐，小王6罐，小李5罐，小赵2罐．这四人所捐罐头的平均数是多少?

2.一商店出售帽子．图2列出了该商店在前三个星期售出的帽子数．

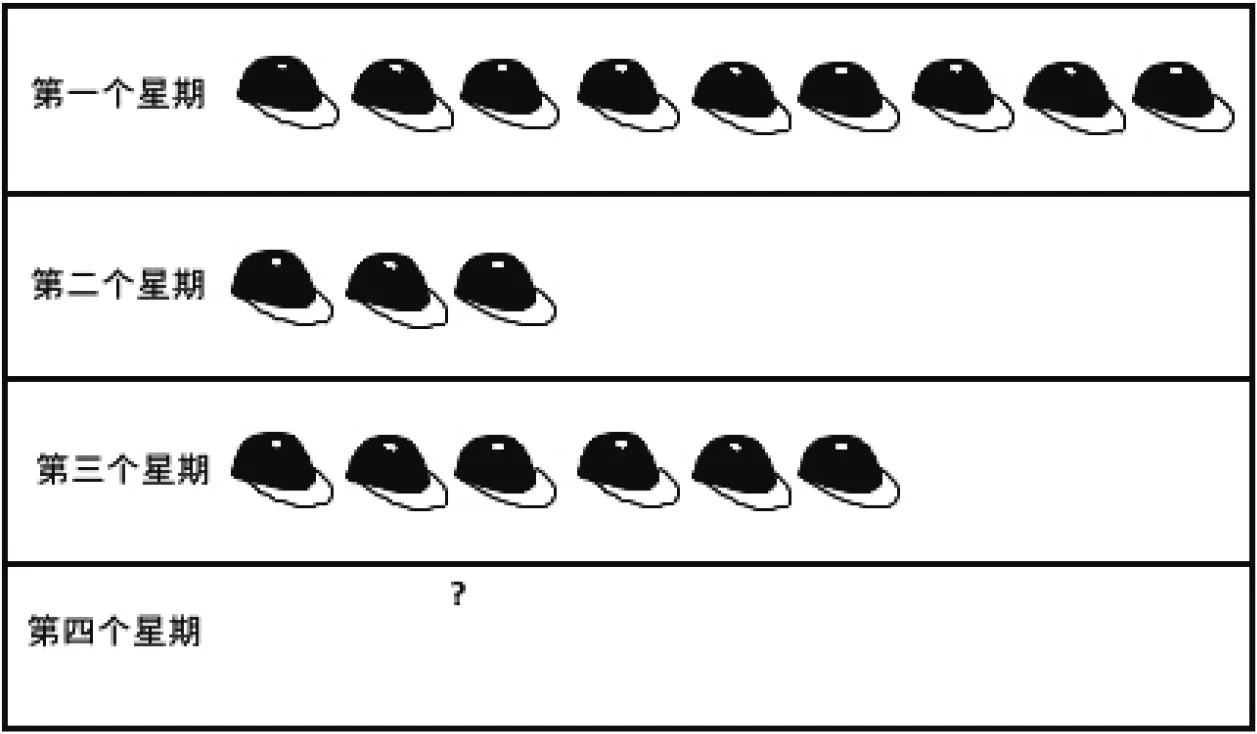
图2 商店每周出售帽子的情况

这家商店在第四个星期应该卖掉多少顶帽子，才能使售出帽子的平均数为7？请写出你的全部解答过程．

研究表明(见表1)，“第一题对但第二题错”的中美学生约占1/4．由此可见，这1/4的学生具有如何计算平均数的程序性知识，但缺乏对平均数算法的概念性理解．随后，对第二题做错的人进行分析，80%以上都知道程序上加一加除一除，但不知道加什么除什么．因为在解答第二题平均数的问题时，学生不能简单直接套用公式求解，他们必须凭借对平均数概念的理解来解答这道题．大多数学生都能认识到平均数的算法是必然会用到的，但往往未能适当地使用那些已知条件，这说明学生并非缺乏程序性知识，而是缺乏对平均数算法的概念性理解，因而不能更灵活地使用这一算法解决问题．因此，在进行实证研究时，需要在理论构架下将现象尽可能的详细、精确地描述出来，并进行分析．

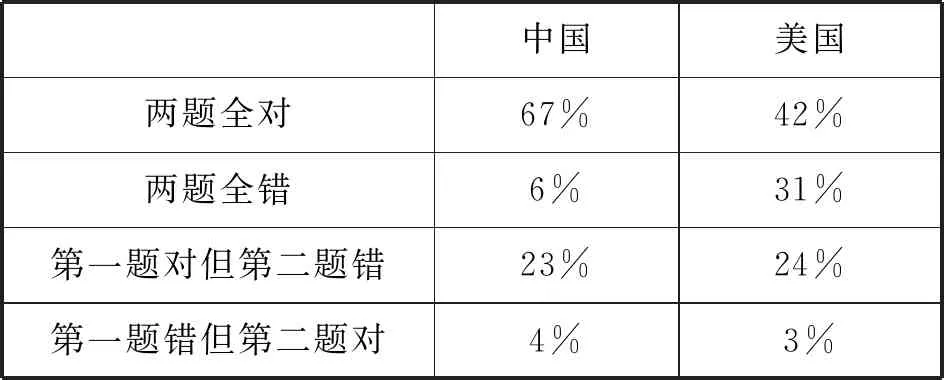
表1 中美学生解答两平均数问题的正确率

第二个例子：美国的改革型(CMP)课程和非改革型(Non-CMP)课程在“解线性方程”的教材编写中到底有何区别？[16]

如何定义变量？改革型课程认为，变量是一个变化的数量，是可以改变的；非改革型课程认为，变量是一个符号或字母，通常用来表示数．如何定义方程？改革型课程认为，含有变量或未知数的等式叫方程．该课程从函数的角度来定义方程，强调用变量来表示数量之间的关系，例如，“寻找表示变量之间关系的变化规律”“理解变量是一种可变化的量，认识现实世界中的变量”“确定变量及自变量、因变量的取值范围”，这些都要求学生通过变量来表示关系；非改革型课程认为方程是含有等号的一个式子，它以代数结构为核心，强调代数运算过程及其背后的结构和模式．为了找到改革型课程与非改革型课程的区别，研究者对初中三年课程中涉及到方程的题目进行分类，发现主要有“含有一个未知量的方程”“二元一次方程”和“二元一次方程组”这三类(参见表2)．

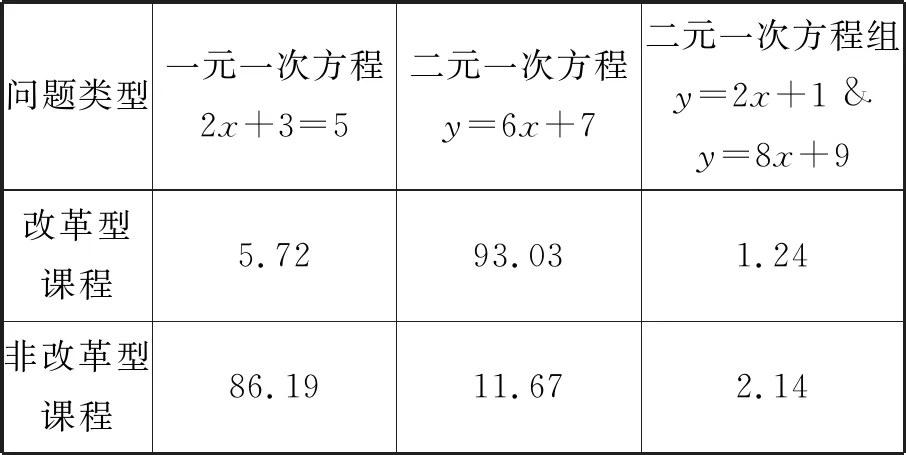
表2 两种课程中涉及线性方程问题的百分比分布(%)

由表2可以发现，在改革型课程中，二元一次方程占比高达93.03%，一元一次方程与二元一次方程组占比仅有7%左右；而在非改革型课程中，占比最高的是一元一次方程，高达86.19%，其余两类约占14%．这说明，改革型课程强调理解方程变量之间的关系，而不是获得求解方程所需的技能．因此，方程求解是在讨论线性关系的背景下引入的，且绝大多数线性方程涉及两个变量．

可见，理论框架指导研究问题、研究方法和数据收集的选择，好的研究问题可以明确回答研究问题所需要的数据类型，且必须与先前的研究或文献相关．因此，通过文献可知，改革型课程采用“功能方法”解方程式，它既强调了情境与语境中改变与变化的重要思想，也强调变量之间关系的表示；非改革型课程则采用“结构方法”，它要求学生抽象地使用符号并遵循系统解方程式的程序．基于先前研究的基础，明确该研究的理论框架，并确定所需收集的数据及数据分析方法，产生令人信服的研究结果，并准确地回答了研究问题．因此，在实证研究中，对数据进行分析的前提是确定理论框架，再由理论框架引导数据分析，并为数据分析的结果作出解释．

3 数据说话与实践智慧

实证研究的目的在于透过表面现象看某一事物(事件)的本质及原因．然而，一些实证研究中不乏产生走极端的现象，且更偏重于为了数据而数据．

举个有关牙线的故事加以说明[17]．有一系列科学研究专门考察“使用牙线对牙齿是否有益？”，这一结果曾在2016年11月的纽约时报上登出．在对其25项相关文献进行研究后发现，使用牙线并不一定能促进良好的口腔健康．换言之，用牙线比不用牙线对牙齿的影响没有统计学上的显著差异．然而，全美牙科协会和普通牙科学会指出，虽然这是在非常严谨和随机控制实验下产生的结果，但实际上，从一系列证据和临床经验中发现，使用牙线对齿间清洁是至关重要的、是有好处的．所以，对证据(数据)的强烈需求是好事，但培养更细致入微的专业知识观应是这一需求的重要部分．

可见，实践智慧是一种能够将一般理论与实际情境相结合的智慧，且实践智慧是教育实践不可或缺的[18]．因此，在研究中，一方面，需要用数据说话；但另一方面，也不要忘记平常的实践智慧．所以，在科学研究中用数据说话是重要的，但不要走极端却忽略了实践中的智慧．有时候，在统计学上产生的偏差只是使用工具产生的结果．例如，在研究学生成绩时，往往会收集身高、年龄、学校等背景变量，然后运用统计软件对这些数据进行相关性分析，来研究其成绩与背景变量是否相关；然而，在实际生活中有些人的身高与成绩是相关的，但有些人并不相关．因此，“实践智慧”是教育实证研究的重要部分，切勿为了数据而数据．

4 数据说话与原因分析

在实证研究中，不仅要考察一门课程、一种教学方法是否有效，更重要的是要看在什么条件下有效．以下面这个研究举例说明[19]．

该研究试图通过调查美国实施新课程学校学生数学成绩的变化情况，来说明新课程的有效性．研究者将20所实施新课程的学校(实验学校)与实施原课程的学校(对照学校)进行一一匹配．从实验学校开始实施新课程的学年起，即从1998年或1999年(部分实验学校从1999年开始实施)至2004年春季学期，调查了所有实验学校与对照学校中学生的数学成绩．通过统计分析、对比研究后发现，20所实验学校学生的数学成绩平均增长与对照学校学生的数学成绩平均增长相比，并没有统计学意义上的差异，也就是说，所实施的新课程并不能更好地促进学生数学学习．研究者推测，新课程的实施也许受到学校及教师改革意愿的影响，换言之，学校和教师强大的改革意愿可能会促进新课程实施的影响，改革意愿低的学校或教师可能会阻碍实施新课程的影响效果．随后，研究者又对所有实验学校增加了一项以“改革意愿”作为变量的调查，调查结果如图3所示．

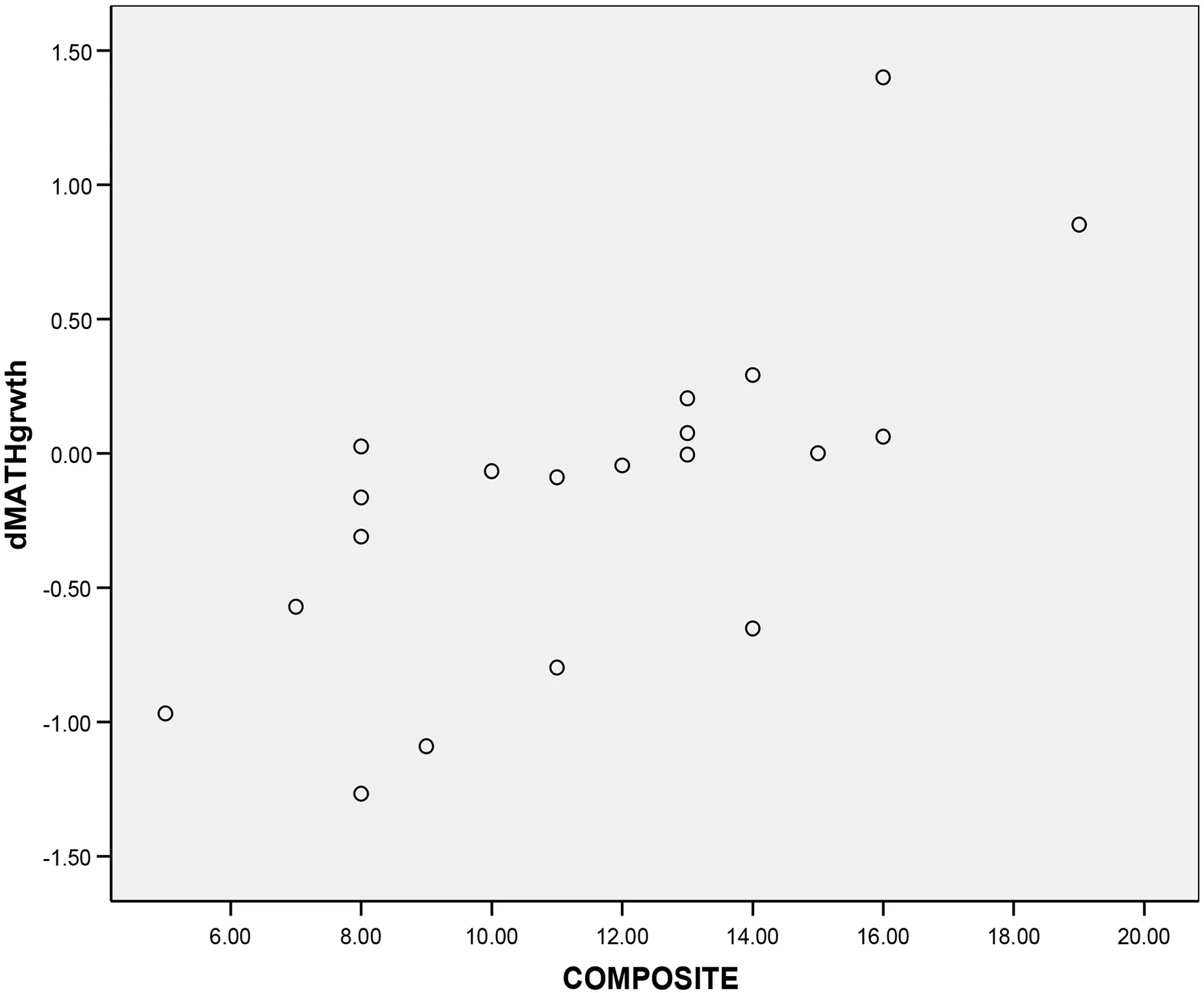
图3 从起始年(1998年或1999年)至2004年，实验学校的数学成绩增长减去与其相匹配的对照学校的数学成绩增长(dMATH growth)，与综合改革意愿分数(COMPOSITE)的函数．

通过图3可以发现，与所匹配的对照学校相比，在改革意愿上得分越高的实验学校，其学生数学成绩就会越高；而实施了新课程但改革意愿较低的学校，其学生的数学成绩低于与其匹配的对照学校学生成绩．换言之，有较强改革意愿的学校，在采用了新课程之后，该校学生的数学成绩有了显著提高；反之，改革意愿较低的中学，在采用新课程之后，数学成绩却大幅下降．

通过上述例子，可以发现，单从总体实验学校的效果来看，并不能准确地说明新课程的实施是否有效．而从不同条件或角度来考察、衡量数据结果，也可以发现新课程实施的实验效果．因此，在回答研究问题时，需要关注研究问题的不同侧面及相关条件，从不同角度解释数据与数据之间的关系，而不仅仅只是关注最直接的研究问题本身．

5 非认知能力——实证研究的重要内容

实证研究不仅要关注个体的认知能力，还应该关注非认知能力的发展．因为对非认知能力的正确认识与理解，直接关系到我国教育的成败和我们所培养人才的素质与规格[20]．近年来，非认知能力在预测教育成就、就业、健康、犯罪趋势等广泛的工作、生活方面显得越来越重要[21-22]．尽管一些国际大型教育研究测试已将非认知能力的影响作用纳入到研究中，但实际上，通过近20年发表在JRME上的研究报告或简要报告来看，只有10%的研究者将学生的非认知能力作为影响学习结果的因素/变量．但值得高兴的是，不少研究者越来越强调非认知能力发展的重要性．例如，Lindqvist和Vestman[23]通过对瑞典14 000余名18岁入伍男性进行了认知能力和非认知能力两方面的测试．20年后，通过调查他们生活状况的各个方面，来研究劳动力市场与认知能力和非认知能力之间的关系．研究发现：认知能力虽然是劳动力市场成功的重要预测因素，但并不是唯一的因素；非认知能力也会影响未来劳动力市场的成功与否．事实上，非认知能力的总体影响大于认知能力(见表3)．该表中选取工资、就业率和失业率3个指标进行解释说明．就工资情况而言，18岁时，如果A比B在认知方面的分数高一个标准差的话，20年后(38岁时)，A的工资很大程度上会比B的工资高5%；而如果A比B在非认知方面的分数高一个标准差的话，20年后(38岁时)，A的工资很可能会比B的工资高9%．就业率和失业率在认知和非认知能力方面也存在类似的差异．换言之，非认知能力比认知能力对工资、就业率和失业率的影响更大．

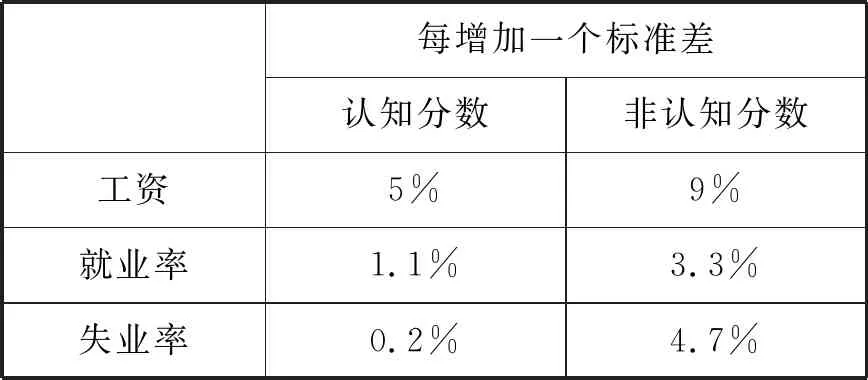
表3 认知和非认知评分中增加一个标准差，20年后其工资、就业率增长和失业率下降的的百分比[22]

Cai和Morris[24]等人也强调：一是教育研究中不仅要考虑认知层面的因素，也要考虑非认知层面的因素；二是不仅要通过短期效应来衡量影响效果的大小，还要通过长期效应来衡量，且长期效应也需要考虑认知和非认知两个层面所产生的影响．

Moyer等人[25]在Lie Cai项目中也从认知和非认知方面对学生数学态度进行了测试．首先在初中6-8年级学生中分别使用改革型、传统型两种不同的课程进行教学，长期跟踪到12年级结束，测试使用不同类型数学课程的学生在数学态度上的差异．研究发现：使用改革型课程的学生，其测量的认知因素所改变的敏感性不如用非认知因素来测试长期的影响来得敏感．换言之，初中分别用两种不同的课程进行教学，到12年级后，这两组学生在成绩上有一些差别(改革型的好一些)；但是，在数学的情感方面，用了改革型课程的学生远远比用了非改革型课程的学生来的更正面、积极．

研究中我们往往只是将非认知方面的因素顺便测一下，而主要关注其在认知方面的变化．通过这两个典型研究案例可以发现，今后的发展方向是将非认知能力的改变作为一个干预来衡量其在认知能力的变化．换言之，今后无论是心理学还是教育学等领域，通过干预学生的非认知能力来提高认知能力都将是新的发展趋势．

6 结束语

实证研究是当今国际教育研究的主流话语和主要方法，相比之下，我国教育实证研究数量少、质量弱的现况表明了加强教育实证研究的必要性和迫切性[4]．目前，我国教育实证研究尚处在艰难的起步阶段，在国际研究舞台上的“声音”亦是微乎其微.因此我国数学教育研究亟需更多、更规范、科学化和高水平的研究成果来提高中国教育研究在国际舞台上的地位和影响力．由此，作为数学教育研究者有必要清楚地了解数学教育实证研究科学、规范的研究范式，避免陷入实证研究误区．基于此，结合多个实证研究案例，提出五点关于数学教育实证研究的建议，希望能够帮助研究者产出更多科学、严谨、高质量的研究成果．