基于学生数学交流能力的微思考

范建兵 (江苏省苏州高新区景山实验初级中学校 215000)

许 彬 (江苏省苏州中学园区校 215000)

国际学生评价项目(PISA2012)的数学测评框架中，数学素养由三种教学过程和七种基本能力构成．七种基本能力为：交流，数学化，表征，推理和论证，设计问题解决策略，使用符号、公式、专业语言和运算，使用数学工具．在这七种基本数学能力中，交流既是构成其他数学素养的基本要素，又是发展其他数学素养的基本途径之一，因为只有学会数学交流，并且不断提高数学交流的深度，才能使学生达成对数学知识的理解，促进数学思维的发展，提升学生的数学素养[1]．现结合许彬老师执教的苏科版教材八年级上学期第二章第5节“等腰三角形的轴对称性(第1课时)”的教学片断，谈谈教学中如何培养学生数学交流能力．

1 从“看”到“做”，在实验活动中培养学生交流能力

《义务教育数学课程标准(2011年版)》(下称《课标2011》)进一步提出“学生学习应当是一个生动活泼、主动的和富有个性的过程．认真听讲、积极思考、动手实践、自主探究、合作交流等，都是学习数学的主要方式”[2]．有教研团队调查发现，初中生中喜欢数学交流的只有17.3%，并且随着年级的升高在逐年下降．因此，提高初中生的交流意识，积极培育学生的质疑和合作能力已是课堂教学的重要、迫切任务．

数学交流能力的培养离不开课堂教学活动的实施，问题情境、实验活动都是教学过程中促进师生及生生交流的重要方式，其中情境问题的高质量、实验活动的有效率、教师提问的准确性等都是克服“一看就懂、一做就错”这一尴尬现状的有效途径，都会影响到学生对数学交流的认知和理解．

1.1 在活动中丰富学生“看”的体验

教学片断1 观察与思考．

问题1数学之美无处不在，下列美丽的图案(图1)蕴含了哪些数学知识？

答：蕴含了轴对称的知识．

图1

问题2利用剪纸的方法，老师按照下图(图2)的步骤操作，你觉得老师手中的纸片是什么形状的？

答：等腰三角形．

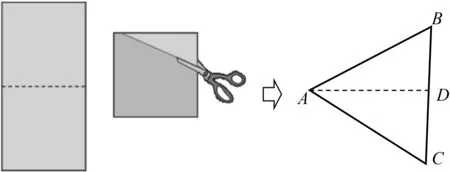
图2

新知识的获得应该是在学生已有知识基础上的自然生长，两个不同层次的“观察”就是由轴对称的生长而来，能够丰富学生“看”的体验．问题1通过回顾轴对称一节中学生共同欣赏过的美丽剪纸，体现数学学习的意义与价值，增强学生对图形之美的理解．问题2通过观察教师剪纸的过程，引导学生进一步结合已有的学习经验，形成图形(等腰三角形)再探究，暗示了等腰三角形的研究与轴对称内容有一定的关联．这样的剪纸示范通俗而易懂，通过观察，大部分学生很容易理解剪纸的目的和依据，为进一步学习与交流奠定了基础．

1.2 在实验中培养学生“做”的能力

苏霍姆林斯基说:“手是意识的伟大培育者，又是智慧的创造者．”动手操作是学生由具体形象思维向抽象逻辑思维过渡的必要手段，是学生手、眼、脑等多种感官协同活动的过程．多种感官参与学习活动，不仅能使学生学得生动活泼，而且对知识的理解更深刻，记忆更牢固，有利于发展学生的数学思维，培养学生的创新精神和实践能力[3]．因此，在实验中培养学生“做”的能力，有利于多视角、全方位地培养学生的数学交流能力．

教学片断2 实验与思考．

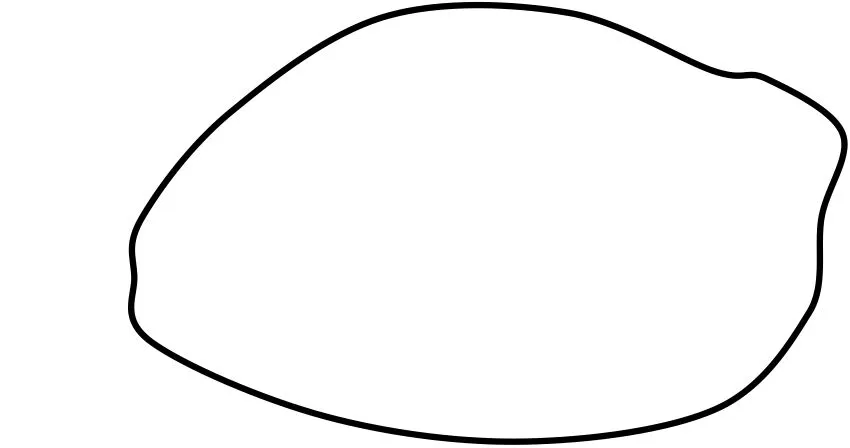
图3

问题3你能利用手中的纸片(图3)，通过折和剪的实验过程，得到一个等腰三角形吗？

问题2的剪纸示范运用的是矩形纸片，问题3的数学实验却是要从一个不规则的图片中剪出一个等腰三角形来．“看”是一种视觉感受，“做”是一种操作体验．“看得懂”不等价于“想明白”，也不一定是“剪得出”，应当让学生经历“思考与思辨”的实验过程，先独立思考，再小组交流自己的操作过程和操作体验，一起归纳活动中的思考与体会．从“看得懂”到“做得出”需要这样的思与剪、说与辨的体验过程，这既能够发展学生的空间观念，有助于发现问题与提出问题经验的积累，也能够提升学生的动手、动脑、动口能力，培养其数学交流的意识和能力．

2 从“说”到“写”，在展示交流中培养学生数学表达能力

《课标2011》在阐述思维能力中指出“要求学生合乎逻辑地、准确地阐述自己的思想和观点”，在解决问题能力中要求“会使用数学语言表达问题，进行交流，形成运用数学的意识”．

2.1 验证性质，培养学生语言表达的能力

教学片断3 猜想与验证．

问题4利用实验操作的方法，大家提出了两个猜想：等腰三角形的两底角相等；等腰三角形顶角的角平分线、底边上的中线、底边上的高互相重合．你能验证这两个猜想的正确性吗？

生1：我将等腰三角形沿底边上的中线所在的直线折叠一下，发现它们有些边和角是重合的，可以直接得到这两个猜想是正确的．

生2：生1这样做并不好，你用实验获得了猜想，再用这个实验来验证性质，这是自相矛盾的．我是这样做的：用量角器和直尺分别量一量有关的边和角，就能够得到这两个猜想是正确的．

教学中通过数学实验让学生归纳、猜想等腰三角形的性质，但猜想是否正确，还需要进一步的验证以及论证．验证的过程可以让学生说一说、辩一辨，尽情地展现学生的思考．你给学生舞台，学生还你精彩．通过数学交流能使学生在学习中充分实现自身的主体地位，充分表达自己的理解和认识，更好地体验数学、体验成功、体验成长．此外，学生还可以通过与老师、与同学的思辨和交流，发现自身的不足，促进自己的思考，促使自己的数学表达更加精炼和严谨．因此，课堂上交流与展示对猜想的各种思考，能够让学生进一步地实现用数学的语言表达问题，是培养学生数学交流素养的重要机会．

当然，度量可能会有误差，教师还可以用更加精准的数学软件进行验证．如果能够借助“几何画板”来动态地展示对猜想的验证，似乎比量一量来得更有说服力．如图4，变化动点A的位置，则两边AB，AC的长度和两角∠B，∠C的度数会发生变化，若有AB与AC的长度相等时，则必有∠B=∠C；如图5，变化动点A的位置，观察两边AB，AC的长度关系与图中底边高线AF、中线AD、顶角平分线AE的分布情况之间的关系，若有AB与AC的长度相等时，则发现三条线段重合．这样的动态呈现带来满满的视觉冲击，能够吸引学生的眼球，在学生心中埋下神奇的数学种子，也让学生进一步理解猜想的合理性．

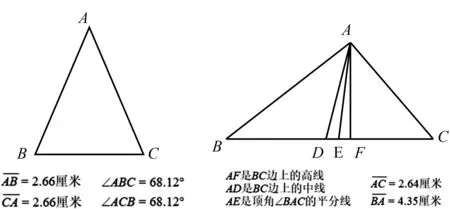
图4 图5

2.2 推理性质，培养学生书面表达的能力

教学片断4 推理与证明．

问题5你能用说理的方式来进一步证明你的猜想吗？

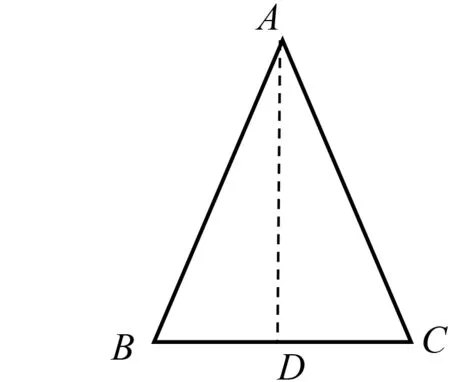
图6

如图6，学生会添加辅助线并用全等的知识来进行证明．

方法1 过点A作AD⊥BC，可以通过HL来证明△ABD≌△ACD，从而得到∠B=∠C．

方法2 也可以作AD平分∠BAC，可以通过SAS来证明△ABD≌△ACD，从而得到 ∠B=∠C．

方法3 还可以作中线AD，然后通过SSS来证明△ABD≌△ACD，从而得到∠B=∠C．

量一量、说一说、看一看，都只是一种浅层次的活动表达，是对性质的初步感知．要想让猜想从合理性走向严密性，将学生的数学思维由直观感知引向严密的逻辑说理，还需要进行推理与证明．

在问题5中，我们要及时追问：如何构造两个三角形全等？如何添作辅助线？还能怎么添？通过追问，让学生体会不同的证明方法，并梳理方法之间的内在关联，让学生在交流中总结与提炼：三种证明方法中的辅助线图形一致，但意义不同．进一步体会等腰三角形的轴对称性，知道底边高线或底边中线或顶角平分线所在直线是对称轴，从而归纳出等腰三角形的两个性质：“等边对等角”和“等腰三角形底边上的高线、中线及顶角平分线重合”．

几何的学习要处理好“三观”问题，这“三观”是图形观、推理观、表达观．图形观指向直观想象素养，就是要培养学生识图、用图、画图的能力和水平；推理观指向逻辑推理素养，要求学生能够区分合情推理和演绎推理，并且能够正确、规范地表达推理过程；表达观指向学习品质，这也是数学交流能力的显性化，是对学生数学学习中的读、写、画、说、证等各个方面的要求．课堂教学中如何规范地表达“等腰三角形的性质”的推理过程呢？从表象上看，这是通过符号语言将学生说理的过程记录下来；从深层次上看，这其实是在呈现性质的由来及其推理的依据，培养学生的逻辑推理能力和分析问题与解决问题的能力．几何学习要重视符号语言的教学，因为符号是进行数学表达和数学思考的重要工具．为了克服学生“会说不会写，想写写不对”的尴尬现状，我们既要解读清楚文字语言、图形语言及符号语言的各自指向及相互转换，更要教会学生用符号语言表达性质的推理过程．数学语言是进行数学思维与交流的工具，三种数学语言的转换，既能培养学生符号意识，也有利于学生在解题中规范答题格式．

数学交流是学生运用数学语言表达概念、定理、方法、问题、思想等，并以此来传递信息与情感，交流媒介是数学语言，对象包括数学知识、问题解决策略、数学情感等[4]．上文中提到的“看、做、说、写”只是课内外师生之间、生生之间用书面、口头形式进行合理推断、表达数学观点的最常用、最基础的交流方式，只是数学交流的部分外显特征．《课标2011》在阐述能力培养时指出：“要随着学生对基础知识的理解的不断加深，逐步提高对基本技能和能力的要求，培养学生独立获取新知识和正确使用数学语言进行数学交流的能力．”我们平时的数学课堂，应该多让学生想一想、画一画、说一说、读一读、写一写、证一证，通过这样最基础的数学交流，学生从感知到认识，从认识到理解，从理解到应用，从应用到素养，为新的认知结构的建立提供根本的保证[5]．这对丰富学生活动经验，夯实学生知识基础，加深学生几何推理，培养学生交流能力都有着积极的意义．