情境教学的核心是去情景

胡祥志 (江苏省南京市中华中学 210019)

由于情境教学更接近于学生的真实体验，很容易引发学生的兴趣以使其产生探究的欲望，因而备受师生青睐．构建情景只是情境教学的前奏，较之于设置什么样的情景，更重要的是如何“去情景化”，以便生成新的学习境地，使学生发现情景背后的数学本质，进入理性的数学科学知识的探索．本文对情境教学中如何“去情景化”提一点建议.

1 问题情景与情境教学

情景与情境是有区别的，“景”是无我而在，“境”是因我而生．“情景”是指“(具体场合的)情形；景象”[1]．“情境”是指“情景；境地”[1]，包括机体本身和外界环境因素相结合的程度和表现情况．本文的情景特指为了数学学习而特别设置的一些生活中常见的景象，是客观存在的．情境是探索这些生活景象之后所生成的更高一级的认知境界，是主观的延伸．情景相对微观，情境相对宏观；情景相对单一，情境相对复合．

问题情景和情境教学既有联系又有区别，它们的思想基础是“万物皆数”(Pythagoras)以及“数学来源于现实，且寓于现实之中”(H.Freudenthal)．问题情景是寻找数学知识在客观世界中的实际背景材料，把数学问题置于学生所热爱的生活认知之中，让学生亲身体验数学的实际创造过程，从而提高学生从生活中发现数学的水平，这是将科学的数学“生活化”．在考试中，问题情景也备受命题者推崇．比如2012 PISA测试的26个题全部都有非常贴近生活、非常自然的情景，对我们探索问题情景的构建和将数学问题生活化的方法有非常高的借鉴价值．情境教学的本质是生活的情景“数学化”．教师不仅要在去情景的过程中有效地组织教学，还要在对情景的提炼和加工中，引发学生的自主探究、自主发现、思维向高阶发展等学习行为.其根本目的是学习数学知识，核心是在去情景的过程中掌握“数学化”的方法．

2 情景构建的数学性

不同情景有不同的看问题的角度，也就有不同的教学效果．教师在构建情景时重点是要保证问题情景的“数学性”，即通常应具有趣味性、阶梯性、易操作性、生活性、体验性、思想性、现实性、挑战性、关联性等．否则，再好的生活问题也构不成问题情景．如关联性，要求问题本身要有一定的数学内涵，体现出一定的数学价值，与教学的目标相辅相成，有“鱼与水”的关联，很容易切中教学目标，切中问题的要害．比如，笔者曾观摩过一节大市级的公开课教学，课题是“三角函数的应用”．上课开始，教师给出了两个情景问题：

(1)2016年10月1日，国庆节的那天刚好是星期六．可否推断出2017年1月1 日，元旦节的那天是星期几吗？

(2)求2×2×…×2(2 016个2相乘)+3× 3×…×3(2 016个3相乘)的个位数字．

从课堂教学的过程看，这两个问题涉及的都是周期问题，和随后的三角函数的应用的教学内容关联不大，所以去情景之后，没有显现任何与本节课教学内容相关联的探究价值．这就不是情境教学．

3 掌握“去情景化”的方法

“去情景化”(decontextualization)是关注生活问题背后的数学本质，将数学知识从具体的生活情景中抽象出来，实现“生活原型”向相应的“数学模式”的转变．

3.1 建“脚手架”，搭起从形象通往抽象的桥梁

很多学生害怕学习数学，这除了数学学科抽象的“天灾”因素，也有教师的“人为”因素．“填鸭式”“题海”等教学方式不仅使学生厌倦数学，还使其没能真正理解数学，导致其从心理上害怕数学、远离数学．然而，他们又不得不去试图学好数学，这就形成了“二律背反”的现象．

有时候，学生可以记住概念、公式，会解题，但不能真正地理解数学里的定义、定理，教师会解释、会证明，但很多学生感觉证明和自己无关，也听不懂；教师在抽象的数学世界里，学生在现实的世界里，教师认为理所当然的事情，而学生却心存疑虑．因此，教师不能只进行抽象的解释，还要逾越感性，为学生指明从现实世界走向抽象世界的路径，搭建起从感性的形象世界通向理性、抽象的思维世界的“脚手架”．

例1平面向量基本定理的教学．苏教版必修4[2]中给出了这样的情景：火箭在升空的某一时刻，速度可以分解成竖直向上和水平向前的两个分速度，在力的分解的平行四边形法则中，得以看到一个力可以分解为两个不共线方向的力的和．教材随后设问：“平面内任一向量是否可以用两个不共线的向量来表示呢？”

应该说情景设置得很好，符合学生的生活认知又有科学性和跨界整合．学生隐约感觉到情景背后隐藏着深刻的道理，但问题的提出有点突兀，为什么有这个问题？这个问题和情景之间有什么联系？如何去情景，要达到什么样的“境”？对于如何从情景中抽象出这个原理，学生感到茫然、困难.这是因为情景和要探索的问题之间缺少台阶．此时，教师去情景就要不断架设“脚手架”，为学生抽象出数学原理搭桥．

先从学生拿手的具体问题开始．

探究1两个人提一个20 kg的物体，他们的用力方向与水平方向成60°角，物体保持平衡，两人各用多少力？

学生很容易解决这个问题．

探究2两个人提一个20 kg的物体，如果一个人的用力方向与水平方向成45°角，另一个人的用力方向与水平方向成30°角，物体保持平衡，两人各用多少力？

问题更进一步，学生能够解决．有了这两个熟悉的问题作铺垫，就可以进入抽象原理的探究了．

探究3平面内给定两个不共线的向量a,b，你能利用这两个向量作出一些向量吗？

有了探索1、2的基础，学生轻而易举地作出了向量a+b和a-b．

探究4你能作出a+3b和2a-b这两个向量吗？

有数乘在里面，问题更进一步，为“有限”个向量向“无限”个向量的跨越作准备．

探究5你能以这两个向量为基础作出无数个向量吗？

学生很快理解通过数乘进行向量的“伸缩”．这又做好了从“无限”到“任意一个”的铺垫．

探究6平面内任一向量c，都能用a,b表示吗？

至此，问题已经非常明了．通过这样的去情景，不断地搭“脚手架”，使学生迈过一个个“台阶”，进入抽象的思维隧道，数学原理也就显现出来，生成新的认知境界．

数学的概念、原理是通过大量现实的、直观的事物抽象出来的．去情景要显现一种抽象的过程，将情景背后的数学本质外显．这个过程中重要的方式是“搭桥”，搭起学生由直观到抽象的“脚手架”，这也是通常说的思维的层次性，表现为一系列的“台阶”.台阶间的潜在距离往往左右着学习的效率，距离远的学生理解不了，距离近的吊不起胃口．所以教师要把握好生活情景和要探究知识之间的潜在距离，让学生“跳起来摘桃子”．

事实上，我们生活中接触的都是具体的实物，都是很形象的，可以促进抽象思维的发展与建立，而抽象思维是形象思维的高级阶段，情境教学的关键便是找到从形象到抽象的路径．

3.2 深层透视，数学思想方法为探究主线

情境教学重在引发学生的数学思考，在理清情景所包孕的数学知识、原理的同时，返璞归真发现问题的结构特征及规律性，让数学思想方法得到理性升华，逐步渗透数学方法论．

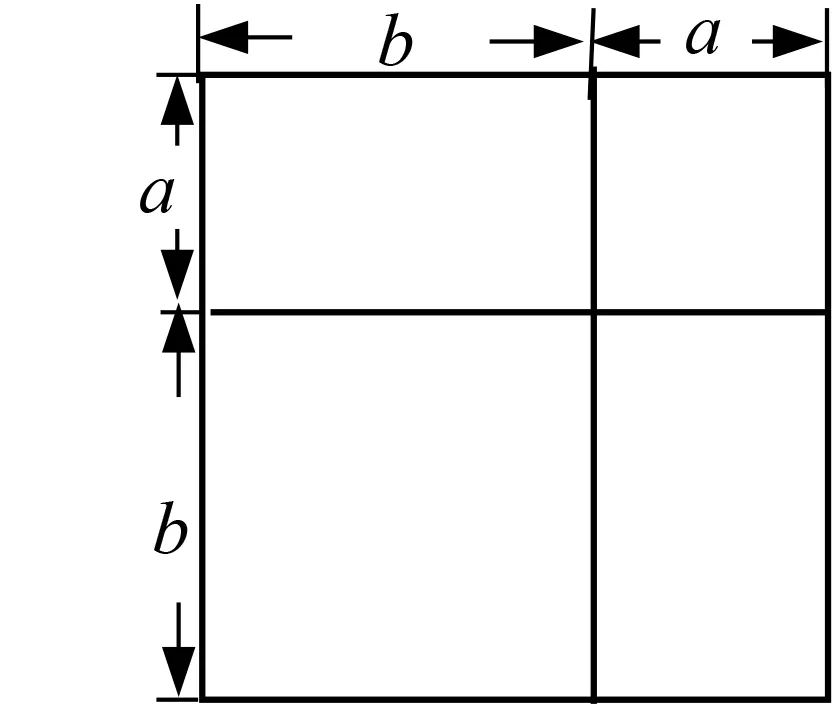
图1

例2苏科版数学七下9.4乘法公式的教学．教材中给出了这样的情景[3]：如图1，大正方形的面积为(a+b)2，2个小长方形和2个小正方形的面积之和为a2+2ab+b2，由此得到(a+b)2=a2+2ab+b2．

情景设置得非常巧妙，古为今用，很有趣、很直观、很简洁．但是如果情境教学仅限于发现这个公式，就可惜了这个情景了．这是一次感悟数学思想方法的绝佳时机，教师可以从以下几个方面引领学生进行探索：

(1)早在毕达哥拉斯时代就用“几何代数”取代了古巴比伦的“算术代数”，现代还在用的一些数学思想可以追溯到四千年以前，这是个逐步发展完善的过程．

(2)可以附带用类似“几何代数”的方式探索乘法分配率公式，如a(b+c+d)=ab+ac+ad，推进对这种方法的认识．

(3)这个情景和教材中的平方差公式的情景浑然一体(如图2，大正方形(边长a)面积减去小正方形(边长b)面积等于右侧大矩形面积)．这两个公式的推导可以同时进行，以便实施“整体教学”以形成系统的方法论意识，不必将两个内容强行肢解后进行教学．

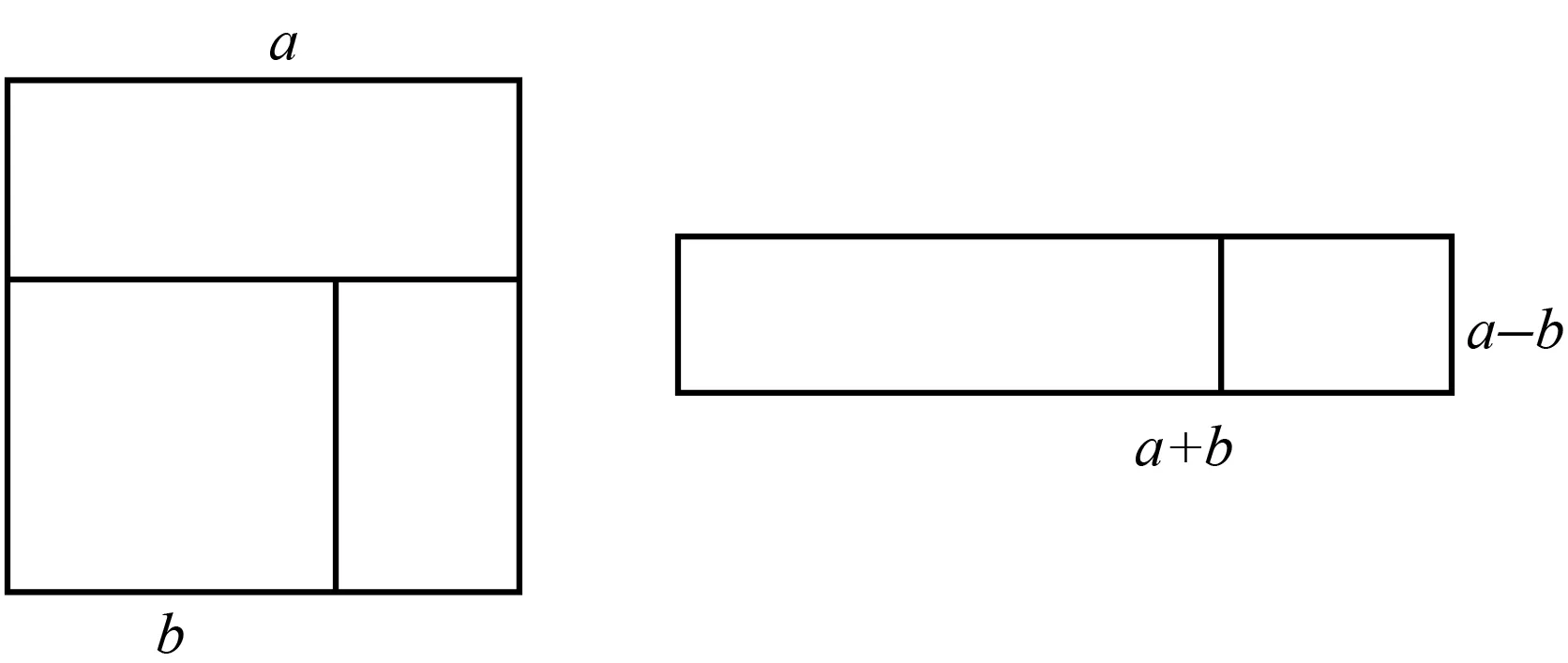
图2

(4)此情境教学的重点是感悟“数形结合” “等价转化”“分割、补形”等重要的数学思想方法．

可以说，数学思想是数学大厦的骨架，拥有对数学思想方法的深入认识是一个人数学素养的重要组成部分，而对于数学思想方法的接受是一个需要慢慢体味的过程，有时要求教师作高屋建瓴的提醒和引领．

3.3 回归传统，感受数学文化的熏陶

很多数学名题都是历史的积淀，在当时的历史条件下名噪一时，给数学打上了浓厚的文化烙印，它们也是人类文化的重要组成部分．利用这些名题构建问题情景时，要重现这些问题的现代数学价值，使学生得到优秀的精神文化熏陶．

例3解二元一次方程的教学．我们设置了这样的教学情景：在数学史上，人们首先解决了形如x3+px=q(*)的方程，然后，把一般的带有二次项的三次方程，通过变换将二次项消去，化归为形如(*)式的方程，从而可解．类似地，在解四次方程ax4+bx3+cx2+dx+e=0(**)时，将其化简为y4+py2+qy+r=0的形式，这样类型的方程是能解的．由此，你能给出一元二次方程ax2+bx+c=0的解法吗？

在去情景的过程中，我们回归传统，重点关注以下几个方面：

(1)研究情景信息，解决提出的问题．用史料让学生明白解三次、四次方程的关键是消去二次项、三次项．那么，解一元二次方程的关键就是消去一次项．

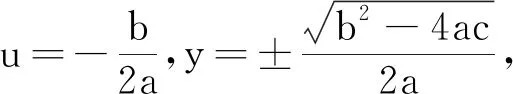
(2)早在美索不达米亚人时代，人类就掌握了特殊的二次方程和三次方程的解法．

(3)解题过程中的换元法，古巴比伦人已经在使用．

(4)在古巴比伦人的一本“难题集”中就有关于二次方程的记载：“已知一个正方形的面积与边长的差是870，求这个正方形的边长．”列方程就是x2-x=870，并且已经有了这类方程的求根公式．

(5)古埃及人会解方程x2+px=q，x2=px+q，x2+q=px(这里的p,q都是正数)，因为没有负数的概念，他们对现在的一般二次方程ax2+bx+c=0大多束手无策．

在这个去情景的过程中，我们从数学史中寻求问题之解，并介绍了一元二次方程解法的演变，让学生很好地领略了数学文化．教育不是一个讲座或一个活动所能一蹴而就的，它需要教学过程中每个契机的浸润．

现代数学教育是将数学置于人类文化大背景下对其进行哲学的反思，它是人类文化的重要组成部分，对人类智力、美学和道德方面有着培养的功能．数学文化已经超越了专业研究范畴，当其广泛进入基础教育，就有了急切的教学要求，高考也明确提出要增加数学文化的考试内容．如何把数学文化形态转化为教育形态，这是值得深思的.但可以肯定的是，数学文化的传承是潜移默化的过程，在去情景中渗透数学文化也是一种可行的方式．

3.4 以“建”代“去”，让学生自己构建问题情景

一般认为问题情景的构建是教师的事情，学生只要去观察、分析、解决就行了，这是“做好了饭给学生吃”.教师可以尝试“让学生自己做饭吃”，由学生自主构建问题情景．相对于去问题情景，构建问题情景更难.前者是相对被动地解决问题的过程，而后者不光要主动发现问题，而且还要能找到解释、解决问题的手段，是思维由低阶向高阶发展的一个飞跃．

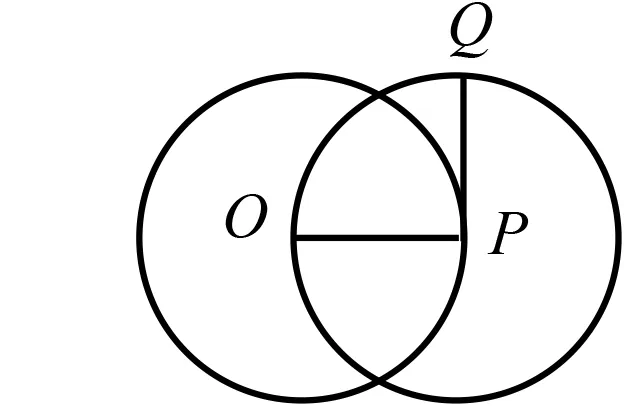
图3

例4在“两角和与差的余弦”(苏教版必修4[2])教学时，给出了这样的问题：“点Q在半径为1的圆P上运动的同时，圆心P又在另一个半径也为1的圆O上运动．O为定点，P,Q两点的初始位置如图3所示，其中OP⊥QP，且P,Q两点以相同的角速度沿逆时针方向运动，这时点Q的运动如何刻画？

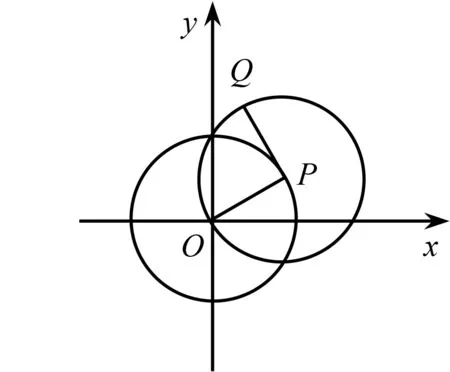
图4

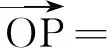
这仅仅是提出了“两角和与差的余弦”如何展开的问题.如何紧扣课本展开教学，需要构建新的情景．课本的证明是用向量的数量积来完成的，这种证明的出现非常突兀．教学中，我们尝试引领学生通过自主构建情景来完成学习．

以下是师生对话中提出的几个关键问题：

(1)前面我们是如何推导同角三角函数和诱导公式的？

此问的目的是回忆过去，找到灵感，思维由过去向现在迁移．学生回忆出利用单位圆来推导，单位圆是研究三角函数的重要载体，本例上述的探究过程也是以单位圆为基本载体．

(2) 学习三角函数之后又学习了向量，现在又回到三角函数，想想，有什么值得借鉴的地方？

本例中，上述探究过程就是将向量的数量积作为重要的探索工具．此问目的是再次从上述探究中寻求灵感，寻找三角函数、向量之间的跨界整合和迁移．

(3)向量的哪部分知识与角的余弦联系得更紧密？是哪个知识点？

从上述探究过程不难看出是数量积，这是找准知识联系的关键点．

(4)要构建情景探索这个公式的证明，有哪些关键的信息？

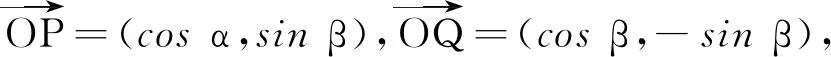
这是一个逆向思维的过程，构建问题情景的过程已经蕴含了公式的发现历程，但构建过程远比解决问题更为困难也更为重要．

4 结语

在去情景过程中，学生可以感受到问题的存在，特别是问题背后蕴含着什么样的深刻道理．这些在学生的头脑中原本可能只是一些模糊的印象，教师要当好“移动式脚手架”，引领学生不断提出并解决新的问题，最终确定情景的本质指向，发现新的数学概念、规律、事实、定理，同时在这个过程中渗透数学方法论思想，使学生感受数学审美，领略数学文化.这就是情境教学“去情景化”的价值．