现象教学视角下的任意角教学实录与反思

孙四周 (江苏省苏州市吴江盛泽中学 215226)

1 教材和学情分析

1.1 教材分析

所用教材为《普通高中课程标准实验教科书·数学(必修4)》(苏教版)，第1章“三角函数”第1节，是整个高中三角函数的起始课．任意角是对初中角概念的推广，也是二维角的最终推广，它是建立三角函数概念的基础．

若从知识教学的角度看，任意角在整个教材体系中不是重点内容(因而极容易被学生轻视)．但从现象教学的角度看，“任意角”在两个方面极为体现数学素养，一是知识推广的原则(必要性和可行性)，二是现实问题数学化(数学抽象和数学建模)．三角函数是用来描述周期现象的，而任意角在坐标系内的表示就已经清晰地体现为周期现象．说到底，正因为角本身的周期性，才有了三角函数的周期性．基于这样的分析，本节课有其特有的教育价值．

教学目标 (1)认识角推广的必要性和可行性、理解任意角的概念，会把角表示在坐标系中；(2)给定任意的度数，会判断角终边的位置； (3)给定角终边的位置，能写出角度数的集合．

教学重点 角概念的推广和在坐标系内的表示．

教学难点 同终边的角的集合．

1.2 学情分析

学生来自四星级高中普通班，数学基础较好．习惯于情境教学，能配合老师活动，但主动探究能力、创新能力稍嫌不足．

2 教学过程

2.1 表象感知阶段

师：在观看体操和跳水比赛的时候，我们会听到一些解说词，比如“转体720°”“转体两周半”．

说明此时并不播放体操或跳水的画面，而是让学生自己想象画面．老师讲话慢一点，给学生留出想象的时间．多数学生会边想象边用手比划，老师鼓励他们“精确比划”.

师：“转体两周半”是多少度？

生：(借助于精确的比划，利用“周角等于360°”进行计算)900°．

师：你能在纸上画出900°角吗？

生：(有点不安)画不出．

2.2 具体认识阶段

师：画不出这个角，没关系，我们从能画出的角入手．现在，我们来画下面的几个角，请快一点：

60°,90°,135°,180°,210°．

说明画前面4个角时，学生很得意，情绪高涨，迅速进入了学习状态．而在遇上210°的瞬间，一切都变了.

生：什么？210°？啥意思？从来没听说过啊——

师：是的，是要你们画210°的角．

生：(经过一番纠结，他们有了这样的判断：210°自然是比180°大的)应当是这个样子(图1、图2)．

图1 图2

师：完全正确，数学家们就是这样画的．我们从来没见过210°角，现在却画了出来，是怎么想到的？

生：说不出理由，凭感觉．

说明顺着60°—90°—135°—180°的惯性，有些学生没有纠结，直接就画出了210°角．画出来以后，就想对“自己的创造物”进行逻辑上的确认，“纠结”也是免不了的.

师：我们凭的是直觉，直觉是非常宝贵的，它是一切创造力的源泉．那么，你还能创造出270°吗？

生：(太容易，随手就画出来了)

师：350°呢？(也容易)——390°呢？(超出360°，再次陷入纠结)

(备注：此时还没有给出“任意角”的定义．在没有定义的情况下，学生能画出390°吗？事实是：在稍微的纠结以后他们还真画出来了，纠结的程度比画210°时小多了)

师：还能画更大的角吗？比如750°．

生：能(手在转圈，比划出750°，已经没有纠结)．

师：可以画出多大度数的角？

生：几千度、几万度都可以．

师：角的度数可以是什么范围？

生：从零到无穷大．

说明至此，“角”在他们眼里已经没有了限制．“没有限制的角”和“任意角”，差的似乎仅仅是一个名词而已．但不可以认为学生的认知已经形成，他们目前还处在直觉阶段，还需要严格的定义.

师：确实如此，从零到无穷大任意度数的角都可以画出来．现在，我们可以画出最开头的那个900°角了．

说明此处留足时间，让学生把900°的角准确地画出来．一是回应他们感情上的需要，二是让神经松驰一下，以迎接新一轮的活动高潮.

2.3 意义抽象阶段

师：回过头来看我们画的210°角，为什么你不说它是150°(即图1和图2中210°“旁边”的部分)？

生：因为那个箭头，要是没有那个箭头，可就不好说了．

师：有道理，不能丢掉箭头．可是，我们忙活了半天，究竟什么是角呢？角的定义是什么？

生：(只能回顾初中的定义)从同一顶点出发的两条射线构成的图形．

师：这个定义能描述我们刚才所画的210°和390°吗？

生：不能，这个定义不能区分210°和150°，也不能区分390°和30°．

师：我们把角的范围推广到了任意正数，大大突破了原来角的范围，原来的定义也不再适用了，看样子应当改写．怎样改写呢？

生：(尝试……)

师生：一条射线绕它的端点旋转所形成的图形叫作角．起始位置的射线叫始边，终止位置的射线叫终边(板书)．

师：这个定义，能包容所有的角吗？比如很大的角，十万度的．

生：可以．因为终边可以无限制旋转下去，因此角的度数没有限制．

师：那么，新的定义还包含原来的角吗？推广必须把原来的概念保持住．

生：原来的锐角、直角、钝角都还在．也可以认为是旋转得到的，就是旋转不超过180°．

师：好的．一是继续描述原来的现象，二是描述更多的新现象，这是数学推广的两个原则．问题是，我们把角推广到任意大的度数，有意义吗？生活中有那么大的角吗？

生：有．直升机机翼的旋转，还有大风车、风力发电机……

师：早上骑自行车来上学的同学，说说你的自行车辐条转了多少度？

生：……

说明回归生活实际，回归对世界的认识，也为新知识增加一个“锚点”.

师：确实如此．下面请大家再来画一个角．听好：-30°．

生：“负30°”？什么叫“负30°”？

师：你感觉呢？什么叫-30米你是知道的．

生：嗯，负数是对相反意义的量的描述．一定是有两个相反的方向，规定一个方向为正，另一个就是负．(备注：老师耐心帮助，让学生动手、动脑)

师：如果对问题看不清楚，我们就应该回到角的定义．角是旋转而形成的图形，旋转的方向只有两个——

生师：一个是顺时针方向，一个是逆时针方向，正好是互为相反的两个方向．

师：那么，规定谁为正方向谁为负方向呢？

生：(好像没有标准可依)……

师：逆时针方向和顺时针方向，规定哪个为正哪个为负，决定权在我们自己手里．

生：……

师：国际上通行的规定是：逆时针方向为正，顺时针方向为负．也就是说，这个(比划逆时针箭头)是——正；这个(比划顺时针箭头)是——负．(学生跟随比划正负角)．

师：这样一来，-30°是不是就可以画出来了？

生：(画-30°)

师：再画一个-150°,-400°．

生：(画角)

师：负角的度数可以到多少度？

生：可以到-∞．

师：到目前为止，角的度数是什么范围？

生：从-∞到+∞．

(其实还缺少零角)

师：确定吗？

生：(思考……)

师：在上面的过程：角的度数可以取到所有正数，也可以取到所有负数．那么——

生：还少一个零度．

师：对，现在还没有零度角．你希望有吗？如果有，它该是什么样的？

生：(画图，思考……)．

师：(提示)还是从定义开始吧．

说明回到定义，这是逻辑思维的一条重要法则，要有这样的素养.

师生：如果射线没有经过任何旋转，我们就把它看成零角(板书)．这是人为规定．

师：如此说来，角的度数可以是任意实数，包括正数、零、负数．每一个角都有一个度数，每一个度数也都可以画出一个角．

(至此，“任意角”的概念已经建立)

2.4 形式表达阶段

师：简直太好了，我们可以有任意大小的角．现在，请你画一个100 000°(十万度)的角．

生：(开始兴致很高，以为胜券在握，可动起手来才知道很难：要转的圈数太多了……)

师：我们先来预估一下，画出来的结果应该是图3中的哪一个？

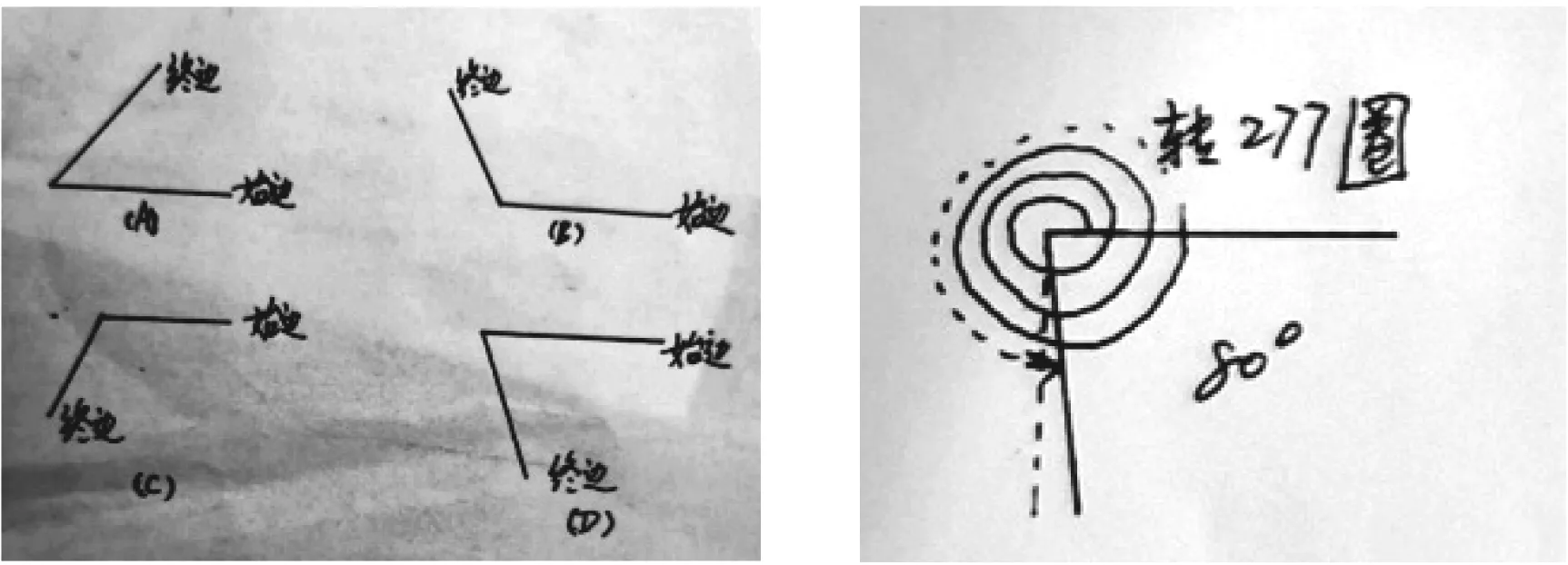
图3 图4

说明图3不是精确作图，只画了始边和终边，那是为了把学生注意力引导到“终边”上，而忽略中间转过的圈数．如果学生能体会到“可以扔掉360°”，那就抽象成功了；如果领会不到，这种图形也可以帮助老师讲解．图3中这些图形本身就是抽象的，图4中那个才是具体的.

师：画始边和终边，我们可以——(齐)忽略360°．不管多少个360°，都不影响终边位置．因此我们应该干什么呢？

生：(活动)……

师：100 000°=277×360°+280°，相当于——(齐)：转过277圈以后继续转280°，于是100 000°的终边和280°的终边相同，因此应该是图3中的选项D．

师：为了便于研究和交流，以后我们常以角的顶点为坐标原点，角的始边为x轴正半轴，建立直角坐标系．这样，角的终边(除顶点外)在第几象限,就说这个角是第几象限角．

说明教这种人为规定的知识，采用告知的方法，不安排探究.

练习(口答)：下面的角分别是第几象限角？是否有终边相同的角？

-300°,-150°,-60°,60°,210°,300°,420°．

思考：锐角是第一象限角．反之，第一象限角是锐角，对吗？(答案：不对)

师：一般地，角的度数增加或减少若干个360°，角的终边——不变．因此，知道一个角α的终边与β的终边相同，这个角的度数并不能确定，而是可以有无数多个值，这些值构成的集合是{β|β=k·360°+α,k∈Z}，这其实也给我们提供了一个判断角终边位置的方法．

2.5 应用巩固阶段

例1在0°到360°范围内，找出与下列角终边相同的角，并指出它们是第几象限角：

(1)650°；(2)-150°；(3)-990°15′．

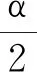
说明例题主要由学生完成，老师强调解题规范，比如k∈Z等.

2.6 回顾与反思，布置作业(略)

3 回顾与反思

3.1 设计理念[1]

这节课，定位不是让学生学会“任意角的知识”而是让他们“对任意角进行刻画”．把学生不认识的角(实例)给他们，将其当做现象去观察、分析，最后生成了新知识、新模式，这就是基于现象的教学．如果是基于知识教学，则有相反的顺序，它会把新知识给学生，再让学生去理解知识、掌握知识、应用知识直至(希望)综合、创新．

对知识进行探究，收获的是知识；对现象进行探究，收获的是对世界的认识．现象教学也收获知识，但那仅是副产品，“主产品”是学生的探究意识和探究能力．知识容易忘记，但探究的意识和能力很难忘记，后者才构成人的内在素养，才是教育应该给予学生的．爱因斯坦、米山国藏和怀特海分别说过几乎相同的一句话：“教育就是当你把在学校里学到的东西都忘记以后还剩下的部分”，现象教学比知识教学能“剩下”更多的东西．

3.2 教学方法[2]

(1)知识生成

经过初中的学习，学生头脑里有了0°—180°角，另外还有一个特殊的“大角”——周角(360°)．从知识上看，周角是最接近于“任意角”的，它似乎处于知识的最前沿．而实际上学生还没有180°—360°之间角的概念，这段空白决定着学生对“周角”的认识不是实在的，360°的意义只停留在“把圆周分成360等份，每一份叫1°角”．因此不能从周角出发引出任意角，我选择用210°和390°作为切入点，来突破180°和360°．

(2)知识表达

在“同终边角的表示”里，我没有按照类似“390°—860°—4 000°—100 000°”这样的顺序“循序渐进”，而是直接让学生面对100 000°(十万度)的角．这是基于这样的考虑：学生在除法运算上不是问题，除法也不是教学的关键，关键是让学生“想到去做除法”，这个“念头”才是核心．好念头应该让学生自己产生，而不是告诉他们让他们“学会”．100 000°，手工操作不现实，便只能去“想”(你可以说学生是“被老师设计”了，也可以说老师发挥了主导作用)．结果是他们“想”了，还从“想”中尝到了甜头，这种学习是快乐的．

十万度虽然是具体的角度数，但这个角不能被直接感知，它几乎等同于抽象角α．不同的是，α不能运算(被360除)，十万度却是可以运算的，这就是选择十万度的理由．当然，如果选择其他诸如5万度、4万度等数字，效果也一样．在学生眼里这些“度”(数)是具体的，但“角”(图形)则不在可感知的范围内，它们具有半具体半抽象的特点．这类对象既便于实际操作又便于意义抽象和创立新模式，是设计现象教学的一项重要资源(因为到这里寻找最近发展区，一找一个准)．可资对比的是，400°就不具备这种特征，因为它太具体，用手转一圈就到了，并不必然导致数学抽象．

(3)核心素养

记住知识，算不得核心素养，核心素养是应对真实世界的能力．“三个会”[3]：会观察、会思考、会表达，宾语都是“世界”．但是我们只能看到“现象”，世界隐藏在现象的背后，于是现象就是我们可以研究的最实在的东西，现象教学的立足点就在这里．

现象的数学化，触及数学本质，有利于提升人的数学素养，选择适合学生的“现象”就是老师必备的业务素养．本节课的后半段，100 000°被看成了现象，这在课的开始是不可想象的．这是基于发展的观点，也是以学生为本的观点．