感悟方程本质，建立模型思想

李静

【摘 要】在小学阶段，就方程的概念学习来说，概念的意义比概念的定义更为重要。史宁中教授认为：一元一次方程比较全面地展示了建模思想——用等号将相互等价的两件事情联立，等号的左右两边等价。这是数学建模的本质表现之一。可见，认识方程的核心在于认识其内在的“等价关系” 模型。我们知道，方程的历史演变经历了文辞式方程、缩写式方程、符号式方程三个时期。教学时，我们可以由方程外在描述性的定义出发，去感悟概念的丰富意义，感悟方程的模型思想。

【关键词】方程的概念 等价关系 模型思想

【教学内容】

苏教版数学五年级下册第1页例1、例2，“练一练”和练习一第1、2题。

【课前慎思】

如何感悟方程本质，建立模型思想呢？本课以苏教版数学五年级下册《认识方程》第一课时为例进行设计。首先，引导学生认识天平，感受平衡，关注等量关系;其次，引领学生共同探究，经历方程概念的形成过程;最后多样练习，深度建模，学生在尝试应用中巩固方程模型。

课前谈话。猜跷跷板谜语，说说玩跷跷板的经验。

师：让我们回到童年，一起用动作体验玩跷跷板。（师生共同用双手做动作，感受平衡、不平衡的状态）

一、认识天平，感受平衡

师：今天我们一起来认识方程。 关于方程，你们有什么问题要问？

生：什么是方程？怎么列方程？学习方程有什么用？……

师：今天，我们重点研究什么是方程，怎么列方程。

师：学习方程离不开一件工具。（出示天平图，图略）认识吗？谁来介绍？

生：这是天平，当天平两边称的物体一样重时，天平就会平衡。

师：像这样，（用双手表示平衡）我们就说天平处于平衡状态。

生：当天平两边称的物体不一样重时，天平就会向左倾斜，或者向右倾斜。

师：像这样，（用双手表示不平衡）我们就说天平——

生（齐）：不平衡。

……

【思考】数学知识来源于生活，数学教学应以学生的认知水平和已有经验为基础。“跷跷板”作为儿童生活中较为熟悉的游戏活动，有着与天平相似的工作原理，作为课前谈话，既可以激起学生的学习兴趣，又可以为后面的学习做铺垫。

二、共同探究，了解方程

（一）用等式表示天平平衡状态

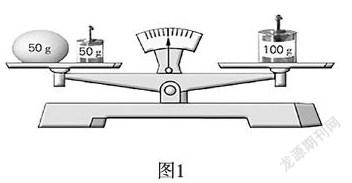
师：你看到了什么？想到了什么？（观察图1）

生：左边一个50克的鸡蛋和一个50克的砝码，右边一个100克砝码，天平平衡。

师：你能用一个式子表示出天平现在的状态码？

生1： 50克的鸡蛋+50克的砝码=100克砝码。

生2： 50克+50克=100克。

生3： 50+50=100。

师：比一比，你最喜欢哪个式子？

生：第三种50+50=100，最简洁。

师：天平左边是50+50;右边是100。图中哪有“=”？

生：天平是平的，（边说边用动作表示平衡）说明天平左右两边相等。

师：我们以前也学过等式，你能举例吗？

（生举例）

【思考】天平直观地呈现，激活了学生的已有经验，学生通过天平的状态用数学语言建构等式及不等式，真正认识到等号的本质意义，表示两边的等价关系。

（二）用含未知数的式子表示等量关系

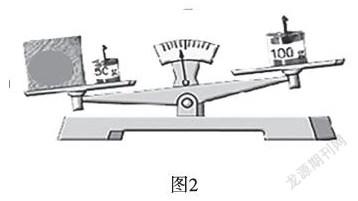
师：在天平左边放一个物体，天平两边物体的质量关系可以怎样表示呢？（观察图2）

生1：这个物体不知道多重。

生2：可以用字母x表示，字母可以表示不知道的数。

师：哦，看来这里的未知数和已知数在一起，有点“已知数”的味道了。

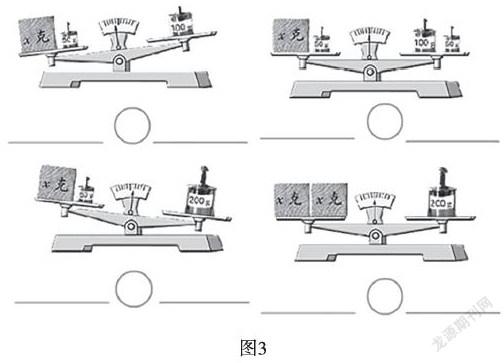
师：为了使天平达到平衡，老师用砝码进行了各种调整，请你用关系式记录你看到的情况。学生在材料纸上完成，并汇报交流。（详见图3）

展示学生记录：（1）一个物体x克+50克的砝码>100克砝码;（2）x+50>150;（3）150-50=x;（4）x+50=150;（5）x+50<150;（6）x+x=200;（7）2x=200。

师：比较一下，你们有什么想说的？

生1：我觉得（2）简单些，（1）的记录比较麻烦。

生2：我认为（3）是在算x等于多少，不是天平现在的样子。

生3：不需要改變未知数的位置，（4）的记录反映了天平的状态，简洁清楚。

生4：我认为（6）的x+x就是2x，（7）的2x=200更简洁。

师：是呀，数学关系式记录，就是用数、符号、字母等进行最简单的表述。

【思考】在教学中引导学生展开观察、比较、交流，学生就能深刻感受到在客观描述天平状态时，已知量和未知量是平等的。同时感受到“=”是描述天平两边的等价关系，而不是以往经验中，从已知到未知的推算。感悟建构方程模型的方法：客观阐述等价关系。

（三）分类、比较，揭示方程的意义

师：你能将黑板上的式子分分类吗？

生1：把相等关系的式子分成一类，不相等关系的式子分成一类。

生2：这些表示相等关系的式子都可以叫等式。

师：今天学的等式和以前学的等式有什么不同？

生：今天学的等式里有字母，以前学的等式里没有字母。

师：像x+50=150、2x=200这样含有未知数的等式就是方程。

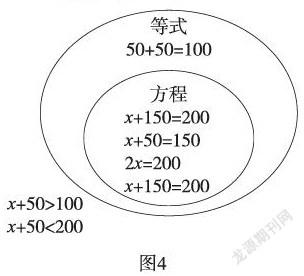
师：老师用一个圈把所有的方程都圈起来，那么，你能圈出所有的等式吗？

展示学生圈的情况（如图4）。

师：没有圈到的可以叫——

生：不等式。

师：看看这两个圈，你们有什么发现？

生1：等式里面包含方程。

生2：所有的方程都是等式。

师（总结）：方程一定是等式，而等式不一定是方程。

【思考】描述现实世界中数量关系的式子有多種，让学生从常见的关系式中，通过观察、比较、分类、抽象、概括逐步归纳出方程的概念，明确概念的内涵与外延，自主建构对概念本质特征的认识。

三、多样练习，深度建模

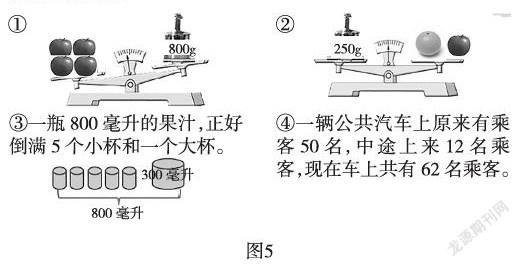
（1）看图列式。（如图5）完成后小组内交流，说说你是怎么想的。

展示：①4x>800;②250=x+y;③5A+300=800;④50+12=62。

生1：我觉得②250=x+y、③5A+300=800是方程，其他不是。

生2：有两个未知数，为什么也是方程？

生3：因为只要是相等的式子，而且含有字母就是方程。

生4：③不是没有天平了，怎么还能列出方程？

生5：因为5个小杯的容量加上300毫升就是总共的800毫升。

师：看来，没有天平了，你们也能找到平衡。这就是数量之间的一种关系，数学上称为——

生（齐）：等量关系。

师：大家都觉得④不是方程，谁能修改一下，让它变成方程？

（生汇报）

师：其实，早在一、二年级时，咱们就已经接触到了方程：（     ）+5=8，（     ）×6=18，（     ）÷5=2。

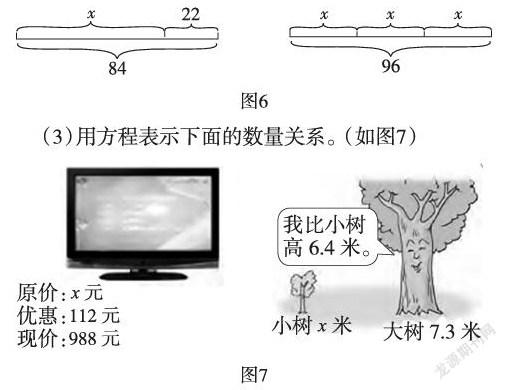
（2）看图列方程。（如图6）

（3）用方程表示下面的数量关系。（如图7）

师：其实，我们生活中的衣食住行等各方面都隐含着很多的相等关系，这些相等关系都能用方程表示出来。

【思考】方程留在学生脑海中的不仅是“含有未知数的等式”这样一句话，重要的是明确列方程的过程，学会把已知数当成未知数一起找等量关系，列出方程，从而深刻建立方程的模型。

四、回顾总结，积累经验

师：同学们掌握得真不错，那学习方程有什么用呢？未知数该怎样求呢？关于方程更多的问题，我们以后继续研究。