关于S-系的正合序列及平坦性

李焕云，王胜杰

(河南师范大学新联学院 公共教学部，河南 郑州 450046)

0 引言

设S是幺半群，一个非空集合A被称作是右S-系，记作AS。如果存在一个映射f:A×S→A,(a,s)|→as,使得对任意的a∈A,s,t∈S,满足(as)t=a(st),a1=1。设A、B是右S-系, 称f:AS→BS是右S-系同态，如果对任意的a∈A,s∈S,满足f(as)=f(a)s。 以下除特殊声明以外，S-系均指右S-系。同样的方法，可以定义左S-系以及左S-系同态。

图1 拉回图 Fig.1 pullback diagram

在图1中作张量积A⊗·,则可得交换图如图2所示。

图2 交换图 Fig.2 Commutative diagram

对于图2中1A⊗f1和1A⊗g1映射的拉回,可取P′={(a⊗m,a′⊗n)∈(AS⊗SM)×(AS⊗SN)|a⊗f1(m)=a′⊗g1(n)}。由拉回定义, 则存在唯一同态φ:AS⊗SP→P′,使得拉回图交换，如图3所示。

图3 拉回图Fig.3 Pullback diagram

定义映射φ(a⊗(m,n))=(a⊗m,a⊗n),对任意的a∈A,(m,n)∈SP，则称φ是相对于A来说相应于拉回图P(M,N,f1,g1,Q)的映射。而所有的平坦性质关系如图4所示。

图4 关系图Fig.4 Relation diagram

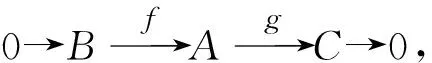
1 主要结果

引理1[6]令S是幺半群,a,a′∈A,b,b′∈B,则a⊗b=a′⊗b′∈AS⊗SB⟺存在自然数m和元素a1,a2,…,am∈A,b2,b3,…,bm∈B,s1,t1,s2,t2…,sm,tm∈S,使得

a=a1s1,

证明假设(x⊗m,y⊗n)∈P(A⊗M,A⊗N,1A⊗f1,1A⊗g1,A⊗Q),其中x,y∈A,m∈M,n∈N,则x⊗f1(m)=y⊗g1(n)∈A⊗Q，如果有a∈A,(m′,n′)∈P(M,N,f1,g1,Q),使得φ(a⊗(m′,n′))=(x⊗m,y⊗n)，则结论成立。

由于x⊗f1(m)=y⊗g1(n)∈A⊗Q,由引理1, 则存在自然数k和元素a1,a2,…,ak∈A,q2,q3,…，qk∈Q,s1,t1,s2,t2,…,sk,tk∈S，使得

x=a1s1,
a1t1=a2s2,s1f1(m)=t1q2,
a2t2=a3s3,s2q2=t2q3,
⋮ ⋮
aktk=y,skqk=tkg1(n)。

(1)

将g作用于式(1)的左列可得

g(x)=g(a1)s1,g(a1)t1=g(a2)s2,s1f1(m)=t1q2,
g(a2)t2=g(a3)s3,s2q2=t2q3,
⋮ ⋮
g(ak)tk=g(y),skqk=tkg1(n),

即g(x)⊗f1(m)=g(y)⊗g1(n)∈C⊗Q,因此得

(g(x)⊗m,g(y)⊗n)∈P(C⊗M,C⊗N,1C⊗f,1C⊗g1,C⊗Q1)。

由假设，对于C，映射φ相应于拉回图P(M,N,f1,g1,Q)是满的，可得存在c″∈C,m′∈M,n′∈N, 使得φ(c″⊗(m′,n′))=(g(x)⊗m,g(y)⊗n),即g(x)⊗m=c″⊗m′,g(y)⊗n=c″⊗n′。因此存在自然数p和元素c1,c2,…,cp∈C,m2,m3,…,mp∈M,u1,v1,u2,v2,…,up,vp∈S,使得

g(x)=c1u1,
c1v1=c2u2,u1m=v1m2,
c2v2=c3u3,u2m2=v2m3,
⋮ ⋮
cpvp=c″,upmp=vpm′。

(2)

又由条件存在g′:C→A,使得g′g=1A。对于式(2)的左列,将g′作用可得

x=g′(c1)u1,
g′(c1)v1=g′(c2)u2,u1m=v1m2,
g′(c2)v2=g′(c3)u3,u2m2=v2m3,
⋮ ⋮
g′(cp)vp=g′(c″),upmp=vpm′,

可得x⊗m=g′(c″)⊗m′∈A⊗M,同理可得y⊗n=g′(c″)⊗n′∈A⊗N,因此φ(g′(c″)⊗(m′,n′))=(g′(c″)⊗m′,g′(c″)⊗n′)=(x⊗m,y⊗n)。

证明对任意a,a′∈A,m,m′∈M,n,n′∈N, 假设φ(a⊗(m,n))=φ(a′⊗(m′,n′))∈P(A⊗M,A⊗N,1A⊗f1,1A⊗g1,A⊗Q)，其中(m,n),(m′,n′)∈P，即a⊗m=a′⊗m′∈A⊗M,a⊗n=a′⊗n′∈A⊗N,f1(m)=g1(n),f1(m′)=g1(n′)。下面只需证明a⊗(m,n)=a′⊗(m′,n′)∈A⊗P,则结论成立。

由于a⊗m=a′⊗m′∈A⊗M,由引理1, 则存在自然数k和元素a1,a2,…，ak∈A,q2,q3,…，qk∈Q,s1,t1,s2,t2,…,sk,tk∈S，使得

a=a1s1,

(3)

将g作用于式(3)的左列，可得

g(a)=g(a1)s1,

即g(a)⊗m=g(a′)⊗m′∈C⊗M,f1(m)=g1(n),同理g(a)⊗n=g(a′)⊗n′∈C⊗N,f1(m′)=g1(n′),因此φ(g(a)⊗(m,n))=φ(g(a′)⊗(m′,n′))。由假设，对于C，相应于拉回图P(M,N,f1,g1,Q)的映射φ是单同态，因此g(a)⊗(m,n)=g(a′)⊗(m′,n′)∈C⊗P,由引理1，存在自然数r和元素c1,c2,…，cr∈C,(m2,n2),(m3,n3),…，(mr,nr)∈P,x1,y1,x2,y2,…,xr,yr∈S,使得

g(a)=c1x1,

又由于存在g′:C→A,使得g′g=1A。对(3)式的左列作用g′可得

a=g′(c1)x1,

g′(c1)y1=g′(c2)x2,x1(m,n)=y1(m2,n2),
g′(c2)y2=g′(c3)x3,x2(m2,n2)=y2(m3,n3),
⋮ ⋮
g′(cr)yr=a′,xr(mr,nr)=yr(m′,n′),

现已证明a⊗(m,n)=a′⊗(m′,n′)∈A⊗P。

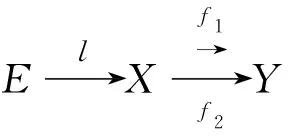
假设a∈A,x∈X,使得a⊗x∈E′,由于a⊗f1(x)=a⊗f2(x)∈A⊗Y,由引理1可得,存在自然数n和元素a1,a2,…,an∈AS,y2,y3,…,yn∈SY,s1,t1,s2,t2,…,sn,tn∈S使得

a=a1s1,

a1t1=a2s2,s1f1(x)=t1y2,
a2t2=a3s3,s2y2=t2y3
⋮ ⋮
antn=a,snyn=tnf2(x)。

(4)

将g作用于式(4)的左列可得

g(a)=g(a1)s1,

g(a1)t1=g(a2)s2,s1f1(x)=t1y2,
g(a2)t2=g(a3)s3,s2y2=t2y3,
⋮ ⋮
g(an)tn=g(a),snyn=tnf2(x),

即g(a)⊗f1(x)=g(a)⊗f2(x)∈C⊗Y,且由于C是均衡平坦的,可得1C⊗f1和1C⊗f2的均衡子是C⊗E, 且g(a)⊗x∈C⊗E,因此x∈E,且a⊗x∈A⊗E。

注记1[9]除了均衡平坦, 通过系统地改变在φ上的必备条件和各种各样拉回的考虑,就可以获得各种各样的平坦条件, 例如, 令A是右S-系, 则证明了

1)φ满足条件(P)⟺对任意的拉回图P(M,N,f1,g1,Q)相应的φ是满同态;

2)A是强平坦的⟺对任意的拉回图P(M,N,f1,g1,Q)相应的φ是单同态;

3)A是满足条件(PWP)⟺对每个拉回图P(Ss,Ss,f1,f1,S)相应的φ是满同态, 其中s∈S。

证明由上述命题1、命题2、命题3，结论显然成立。

定义2[2]称右S-系AS是GP-平坦的，如果对任意的a,a′∈A,s∈S,若在AS⊗SS中a⊗s=a′⊗s,则存在n∈N,使得a⊗sn=a′⊗sn在AS⊗SSsn中成立。

引理2[2 ]令S是幺半群且A是右S-系, 则下列条件等价

1)A是GP-平坦的；

2)对任意的s∈S,a,a′∈A,a⊗s=a′⊗s∈A⊗S,可得存在自然数m,n∈N且a1,a2,…,am∈AS,s1,t1,s2,t2,…,sm,tm∈S，使得

a=a1s1,

a1t1=a2s2,s1sn=t1sn,
a2t2=a3s3,s2sn=t2sn,
⋮ ⋮
amtm=a′,smsn=tmsn。

证明假设as=a′s,其中a,a′∈A,s∈S,则g(a)s=g(a′)s,因此g(a)⊗s=g(a′)⊗s∈C⊗S,由于C是GP-平坦的，由定义2，可得存在自然数n,使得g(a)⊗sn=g(a′)⊗sn∈C⊗Ssn。由引理2，等式

g(a)=c1s1,

c1t1=c2s2,s1sn=t1sn,
c2t2=c3s3,s2sn=t2sn,
⋮ ⋮
cmtm=g(a′),smsn=tmsn

(5)

存在，其中c1,c2,…,cm∈C,s1,t1,s2,t2,…,sm,tm∈S。由于g是满同态， 则存在ai∈A,使得g(ai)=ci(1≤i≤m).因此由式(5)可得

g(a)=g(a1)s1,

g(a1)t1=g(a2)s2,s1sn=t1sn,
g(a2)t2=g(a3)s3,s2sn=t2sn,
⋮ ⋮
g(am)tm=g(a′),smsn=tmsn。

(6)

令a0=a,t0=1,am+1=a′,sm+1=1.则(aiti,ai+1si+1)∈kerg(0≤i≤m),因为kerg≤K(ρ)=1A∪(Imf×Imf)，若(aiti,ai+1si+1)∈1A(0≤i≤m),则式(6)可化为

a=a1s1,

a1t1=a2s2,s1sn=t1sn,
a2t2=a3s3,s2sn=t2sn,
⋮ ⋮
amtm=a′,smsn=tmsn，

即a⊗sn=a′⊗sn∈A⊗Ssn,可得A是GP-平坦的。否则假设k是(6)中使得(aktk,ak+1sk+1)∈Imf×Imf的最小下标，l是(6)中使得(altl,al+1sl+1)∈Imf×Imf的最大下标，则存在bk,bl+1∈B,使得

aktk=f(bk),al+1sl+1=f(bl+1)，因此f(bksn)=f(bk)sn=aktksn=aksksn=ak-1tk-1sn=…=a1t1sn=a1s1sn=asn=

(as)sn-1=(a′s)sn-1=a′sn=amtmsn=amsmsn=am-1tm-1sn=…=al+1tl+1sn=al+1sl+1sn=f(bl+1sn)。

由于f是左可裂的，即存在f′:A→B，使得f′f=1B，则可得bksn=bl+1sn。因为B是GP-平坦的， 则B是主弱平坦的，可得bk⊗sn=bl+1⊗sn∈B⊗Ssn。即存在α1,α2,…,αp∈B,s′1,t′1,s′2,t′2,…,s′p,t′p∈S，使得

bk=α1s′1,

α1t′1=α2s′2,s′1sn=t′1sn,
α2t′2=α3s′3,s′2sn=t′2sn,
⋮ ⋮
αpt′p=bl+1,s′psn=t′psn。

因此

a⊗sn=a1s1⊗sn=a1⊗s1sn=a1⊗t1sn=a1t1⊗sn=…=aktk⊗sn=f(bk)⊗sn=f(α1s′1)⊗sn=

f(α1)⊗s′1sn=f(α1)⊗t′1sn=f(α1)t′1⊗sn=f(α1t′1)⊗sn=f(α2s′2)⊗sn=…=f(αps′p)⊗sn=f(αp)⊗s′psn=

f(αp)⊗t′psn=f(αpt′p)⊗sn=f(bl+1)⊗sn=al+1sl+1⊗sn=al+1⊗sl+1sn=al+1⊗tl+1sn=al+1tl+1⊗sn=

al+2sl+2⊗sn=…=amsm⊗sn=am⊗smsn=am⊗tmsn=amtm⊗sn=a′⊗sn。

可得A是GP-平坦的。

证明在GP-平坦中，令n=1，则可得主弱平坦。

证明由于B,C是弱平坦的，则B,C是主弱平坦的，由上述推论可得A是主弱平坦的，要证明A是弱平坦的,只需证明A满足条件(W)。

令as=a′t，其中a,a′∈A,s,t∈S，则g(a)s=g(as)=g(a′t)=g(a′)t，由于C满足条件(W)，则存在c″∈C,u∈Ss∩St,使得g(a)s=g(a′)t=c″u。由于g是满同态， 因此存在a″∈A, 使得g(a″)=c″。因此g(as)=g(a′t)=g(a″u),即(as,a″u)∈kerg≤K(ρ)=(Imf×Imf)∪1A。

若(as,a″u)∈1A,则as=a′t=a″u,其中u∈Ss∩St,因此A满足条件(W)。否则(as,a″u)∈Imf×Imf,则存在b∈B，使得as=a′t=f(b),由于f左可裂,则存在f′:A→B，使得f′f=1B,因此f′(a)s=f′(a′)t=b。又由于B满足条件(W),则存在b″∈B,v∈Ss∩St,使得f′(a)s=f′(a′)t=b。因此f(b)=f(b″)v,可得as=a′tf(b″)v，其中v∈Ss∩St,即B满足条件(W),因此B是弱平坦的。

证明令a⊗m=a′⊗m′∈A⊗M,其中a,a′∈A,m,m′∈M,则g(a)⊗m=g(a′)⊗m′∈C⊗M，由于C是平坦的，g(a)⊗m=g(a′)⊗m′∈C⊗(Sm∪Sm′),因此存在

g(a)=c1s1,

c1t1=c2s2,s1m=t1m2,
c2t2=c3s3,s2m2=t2m3,
⋮ ⋮
cntn=g(a′),snmn=tnm′，

其中c1,c2,…,cn∈C,m2,m3,…,mn∈(Sm∪Sm′),s1,t1,s2,t2,…，sm,tm∈S。由于g是满同态, 则存在ai∈A(1≤i≤n)，使得

g(a)=g(a1)s1,

g(a1)t1=g(a2)s2,s1m=t1m2,
g(a2)t2=g(a3)s3,s2m2=t2m3,
⋮ ⋮
g(an)tn=g(a′),snmn=tnm′。

(7)

令a0=a,t0=1,an+1=a′,sn+1=1,则(aiti,ai+1si+1)∈kerg(0≤i≤n)。由于序列是准正合的，即kerg≤K(ρ)=1A∪(Imf×Imf)，若(aiti,ai+1si+1)∈1A(0≤i≤n),式(7)可变为

a=a1s1,

a1t1=a2s2,s1m=t1m2,
a2t2=a3s3,s2m2=t2m3,
⋮ ⋮
antn=a′,snmn=tnm′，

(8)

其中a1,a2,…,an∈A,m2,m3,…，mn∈(Sm∪Sm′),s1,t1,s2,t2,…,sm,tm∈S,可得a⊗m=a′⊗m′∈A⊗(Sm∪Sm′)，即A是平坦的。

否则假设k是(7)式中使得(aktk,ak+1sk+1)∈Imf×Imf的最小下标，l是(7)式中使得(altl,al+1sl+1)∈Imf×Imf的最大下标。则存在bl+1,bk∈B,使得aktk=f(bk),al+1sl+1=f(bl+1)，因此可得

f(bk)⊗mk+1=aktk⊗mk+1=ak⊗tkmk+1=ak⊗skmk=aksk⊗mk=ak-1tk-1⊗mk=…=a1t1⊗m2=a1⊗t1m2=

a1⊗s1m=a1s1⊗m=a⊗m=a′⊗m′=antn⊗m′=an⊗tnm′=an⊗snmn=ansn⊗mn=an-1tn-1⊗mn=

an-1⊗tn-1mn=an-1⊗sn-1mn-1=an-1sn-1⊗mn-1=…=al+1sl+1⊗ml+1=f(bl+1)⊗ml+1。

因此，f(bk)⊗mk+1=f(bl+1)⊗ml+1∈A⊗M,由于f是左可裂的,则存在f′:A→B,使得f′f=1B。因此f′⊗1M:A⊗M→B⊗M,其中(f′⊗1M)(b⊗m)=f′(b)⊗m，可得bk⊗mk+1=(f′⊗1M)(f(bk)⊗mk+1)=(f′⊗1M)(f(bl+1)⊗ml+1)=bl+1⊗ml+1∈B⊗M.

由于B是平坦的，可得bk⊗mk+1=bl+1⊗ml+1∈B⊗(Sml+1∪Smk+1)⊆B⊗(Sm∪Sm′)。因此存在

bk=α1s′1,

α1t′1=α2s′2,s′1mk+1=t′1m′2,
α2t′2=α3s′3,s′2m′2=t′2m′3,
⋮ ⋮
αjt′j=bl+1,s′jm′j=t′jml+1。

(9)

其中α1,α2,…,αj∈B,m′2,m′3,…,m′j∈(Sm∪Sm′),s′1,t′1,s′2,t′2,…,s′j,t′j∈S。因此

aktk=f(α1)s′1,

f(α1)t′1=f(α2)s′2,s′1mk+1=t′1m′2,
f(α2)t′2=f(α3)s′3,s′2m′2=t′2m′3,
⋮ ⋮
f(αj)t′j=al+1sl+1,s′jm′j=t′jml+1。

(10)

由(8)(9)(10)式可得

a⊗m=a1s1⊗m=a1⊗s1m=a1⊗t1m2=a1t1⊗m2=a2s2⊗m2=…=aksk⊗mk=ak⊗skmk=ak⊗tkmk+1=

aktk⊗mk+1=f(α1)s′1⊗mk+1=f(α1)⊗s′1mk+1=f(α1)⊗t′1m′2=f(α1)t′1⊗m′2=f(α2)s′2⊗m′2=f(α2)⊗s′2m′2=

f(α2)⊗t′2m′3=…=f(αj)⊗t′jml+1=f(αj)t′j⊗ml+1=al+1sl+1⊗ml+1=al+1⊗sl+1ml+1=al+1⊗tl+1ml+2=al+1tl+1⊗ml+2=

al+2sl+2⊗ml+2=…=ansn⊗mn=an⊗snmn=an⊗tnm′=antn⊗m′=a′⊗m′∈AS⊗(Sm∪Sm′),

因此a⊗m=a′⊗m′∈AS⊗S(Sm∪Sm′)，即可得A是平坦的。

下面针对近来新出现的并且在经典的平坦图表中没有刻画的平坦性质进行讨论，文献[10-11]给出了关于S-系新的平坦性质的等价刻画。称右S-系AS满足条件(E′)，如果对任意的a∈A,s,s′,z∈S,若as=as′,sz=s′z,则存在a″∈A,u∈S,使得a=a″u,us=us′。称右S-系AS满足条件(E′P),如果对任意的a∈A,s,s′,z∈S,若as=as′,sz=s′z,则存在a″∈A,u,v∈S,使得a=a″u=a″v,us=vs′。称a∈A满足条件(WR),如果对于as=at,其中s,t∈S,总存在e2=e∈S,使得ae=a,es=et.如果A中所有元素都满足条件(WR),则称A满足条件(WR)。

若a=a″u时，结论已证。否则(a,a″u)∈Imf×Imf。可得存在b∈B,使得f(b)=a.则f(bs)=f(b)s=as=as′=f(b)s′=f(b′s)。由于f是单同态,可得bs=bs′,sz=s′z。由于B满足条件(E′),可得存在b″∈B,v∈S,使得b=b″v,vs=vs′。取a′=f(b″),则a=a′v,vs=vs′,即A也满足条件(E′),结论已证。

若a=ae时，结论已证。否则存在b∈B,使得a=f(b)，则f(bs)=f(b)s=as=at=f(b)t=f(bt)。由于f是左可裂的,可得bs=bt。由于B是满足条件(WR)的S-系，则存在h2=h∈S,使得bh=b,hs=ht.因此a=f(b)=f(bh)=f(b)h=ah，即A是满足条件(WR)的S-系。