遗传算法优化的神经网络预测团雾
余星辉, 孙晨曦
(1.江苏科技大学 经济管理学院,江苏 镇江 212100; 2.华北水利水电大学 数学与统计学院,河南 郑州 450046)
0 引言
团雾是受局部地区微气候环境影响,在大雾中数十米到上百米的局部范围内出现的更“浓”、能见度更低的雾[1]。低能见度的团雾容易引发包括车辆追尾等在内的交通事故,由于团雾形成突然,传统的气象方法难以对其进行监测和预报,往往难度较大、成本较高,具有极大的安全隐患[2]。王月琴等[3]提出可以利用BP神经网络对高速公路团雾进行预测,但在初始权值设立和网络结构建立时会造成网络震荡,且在计算过程中易陷入局部最优解,仍存在不足[1]。针对上述缺点,本文采用遗传算法对该模型进行优化,使用概率化的寻优办法对数据进行处理,使其自动地适应与调整搜索方向,并对多个个体进行同时处理、对多个解进行评估,以降低陷入局部最优解的风险[4]。
1 团雾预测模型的BP神经网络建模
1.1 BP神经网络简介
BP(Back Propagation)神经网络,是一种模拟生物神经网络的多层前馈网络,它使用最速下降法,通过信息正向传播与误差反向传播对算法进行连续训练。在训练过程中,模型中的权值和阈值不断被自动调整,网络的误差平方和也随之不断减小,直至达到可接受的范围,得到所期望的映射关系。神经网络算法的优点在于无需预先对所求的映射关系进行描述,仅需要提供历史输入、输出数据作为训练样本。
在BP神经网络中,输入信号从各神经元的输入层进入,由隐含层通过激活函数传递到输出层,完成一次正向的学习过程。当实际输出与期望输出之间存在差异时,两者间的误差将由输出层反向传递给输入层,依据梯度下降法调整神经网络各层间的权值与阈值,完成一次反向的学习过程。在正向学习与反向学习交替进行的整个过程中,各神经元的权值和阈值将随之不断地进行调整,直到误差减小到可以接受的范围。
设x1,x2,…,xi为神经元1,2,…,i的输入数据;q、m分别为隐含层和输出层的节点个数;vij为输入层到隐含层的连接权重,wki为隐含层到输出层的连接权重;θi为隐含层阈值,ak为输出层阈值,f(·)为神经网络的激活函数。则隐含层第i个节点的输出为
oi=f(neti),i=1,2,…,q,
(1)
(2)
输出层第k个节点的输出为
yk=f(netk),k=1,2,…,m,
(3)
(4)
输出误差通常定义为
(5)
代入隐含层与输出层数据后可以得到系统的总误差函数为
(6)
1.2 团雾预测模型的神经网络结构设计
本文所使用的模型为3层BP神经网络(图1)。
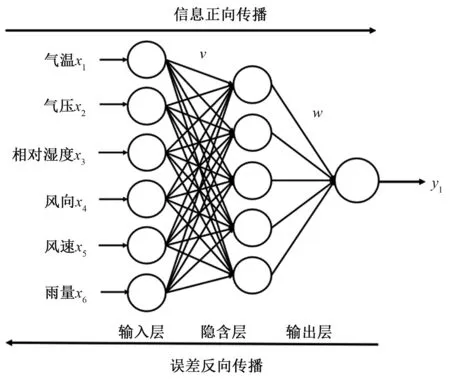
图1 3层BP神经网络结构示意图Fig.1 Structure diagram of three-layer BP neural network
根据分析团雾形成的气象特征,设计了气温、气压、相对湿度、风向、风速、雨量6个输入变量。输出层输出变量设定为1(有雾)与-1(无雾)两种情况。隐藏层的节点个数经验公式
S=a+(m+n)0.5,
(7)
其中S为隐含层的输入向量维数即节点个数,m为输入向量维数,n为输出向量维数,a为[1,10]之间任一常数[5]。经多次实验,本文将隐含层节点个数设置为5,即建立“6-5-1”结构的3层BP神经网络,参数设置见表1。

表1 神经网络参数设置Tab.1 Parameter setting of neural networks
2 遗传算法优化的神经网络
尽管BP神经网络无需事先对所求的映射关系进行描述,仅需提供历史输入、输出数据作为样本对其进行训练便可成功构建。但由于初始权值和网络结构设置的随机性,神经网络的构建过程存在着极大的不确定性。采用遗传算法对神经网络进行优化,对得到的数据采用概率优化方法,使其自动适应调整搜索方向,可以对多个解进行有效评估。在初始阶段需要先将BP神经网络的初始权值阈值编码设置为染色体个体,通过遗传算法不断进行选择、交叉、变异的操作,直至得到最优权值阈值,再代入神经网络中进行训练。遗传算法优化BP神经网络算法流程如图2所示。
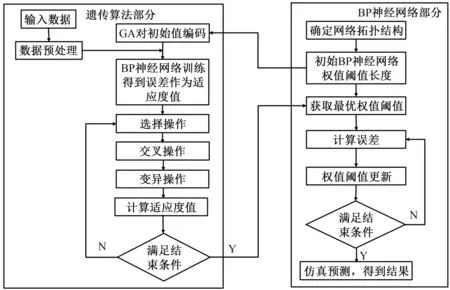
图2 遗传算法优化BP神经网络算法流程图Fig.2 Flow chart of BP neural network algorithm optimized by genetic algorithm
2.1 染色体编码、种群初始化与参数设置
本文采用实数编码方法,在变量的取值范围内随机生成,用于随机初始化一个种群;遗传算法中涉及的各项参数设置见表2。

表2 遗传算法参数设置
2.2 计算适应度函数
个体适应度值用于度量编码个体的好坏。本文将适应度函数F设置为模型实际预测输出与期望输出之间的误差绝对值之和,此时适应度值越小,模型输出的绝对误差越小,模型运算效果越好,即
(8)
其中k为系数,n为网络输出层的输出节点个数,yi为神经网络第i个神经元的期望输出,oi为第i个神经元的模型实际运行输出[6]。
2.3 选择
本文采用轮盘赌的方式进行选择操作,即基于个体的适应度比例设置选择概率,其中每个个体i的选择概率pi为
fi=k∕Fi,
(9)
(10)
其中Fi为个体i的适应度值,k为系数,N为种群个体总数。
2.4 交叉
交叉操作模拟染色体的重组过程,在交叉过程中,染色体个体的选择和具体交叉位置的选择均为随机。本例中染色体个体采用的编码方式为实数编码,采用的交叉操作方法为实数交叉法[6]。第k个染色体ak和第l个染色体al在第j个基因位所进行的交叉操作为
akj=akj(1-b)+aljb,
(11)
alj=alj(1-b)+akjb,
(12)
其中b为[0,1]间任一随机数。
2.5 变异
变异操作模拟生物遗传进化中的基因突变过程,有利于防止算法在运算过程中陷入局部最优解[6]。第i个个体在第j个基因的变异操作为
(13)
其中amax、amin分别为基因aij的最大值与最小值,f(g)=r2(1-g∕Gmax)2,r2为系数,g为遗传算法当前的迭代次数,Gmax为事先设置好的进化代数,r为[0,1]之间的任一随机数[7]。
3 模型预测结果分析
本文采用沪宁高速公路沿线某气象监测站的13组历史团雾数据,取其中10组作为训练集,用于调整网络的权值和阈值;取其中3组作为验证集。对输入神经网络的数据进行归一化处理,以消除数据间度量单位所带来的影响,加快程序的收敛速度。数据归一化的公式为
(14)
其中x为收集到的原始数据,xmin为样本数据最小值,xmax为样本数据最大值。
将归一化处理后的数据输入所建立的遗传算法优化的神经网络中进行训练,利用遗传算法优化的过程中得到的适应度曲线如图3所示,其中显示的最佳适应度为0.009 4。经过计算,得到最大误差为0.018%,即该模型具有较好的实验效果。

图3 遗传算法寻优适应度曲线Fig.3 Genetic algorithm optimization fitness curve
4 结束语
由于影响团雾形成的因素众多且往往与局部地区气候环境关系密切,难以对团雾的形成进行及时的预警评估。现有的基于BP神经网络的团雾预测模型,由于初始权值和网络结构确定过程中的随机性使得在网络建立过程中存在着较大的不确定性,而且在计算过程中易陷入局部解。对此本文使用遗传算法对神经网络初始权值和阈值加以修正,在解决上述问题的同时也加快了算法的收敛速度,建立了基于GA-BP算法的神经网络团雾预测模型。实验仿真结果表明,预测结果误差较小,为团雾的实际预测应用提供了新的方法与思路。

