航空用GH625镍基高温合金带材的成形极限研究

肖纳敏，雷宇2，罗俊杰2，孔祥任2，王振2，贾崇林，沙爱学

（1.中国航发北京航空材料研究院，北京 100095；2.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082）

GH625是一种镍基高温合金，具有出色的高温综合力学性能，在核能工业、航空航天以及石油化工等领域都有广泛应用[1]。镍基高温合金的成形工艺参数域较窄，成形控制难度大[2]。国内现阶段主要采用轧制方法生产镍基合金板材，轧制工艺使镍基合金板材呈现各向异性的特点，给GH625高温合金的成形极限图的获取带来了巨大的挑战。成形极限是表征板料在进行成形时所能够达到最大成形能力的指标，该指标可以为成形工艺方案的制定以及成形工艺优化提供指导，促进了板料成形研究和零件开发的进步。获取成形极限图的方法有许多种，主要可以分为理论计算、试验确定和数值预测方法[3]。

在理论预测方面，Swift[4]和Hill[5]首先分别提出了分散性失稳和集中性失稳模型，这两种模型都假定金属薄板是不存在初始缺陷，随应变增加，材料不再均质。为考虑应变硬化过程中板材出现的非均质情形，Hora和Tong[6]在Swift模型基础上提出修正最大荷载准则（Modified maximum force criterion,MMFC）。Marciniak和Kuczynski[7]则假定板材存在初始缺陷，并基于该假设推导了M-K模型，被广泛使用于FLC理论预测。Sowerby和Duncan[8]（1971）使用二次性屈服准则——Hill'48屈服准则和Swift各向同性硬化模型计算FLC，结果表明FLC右侧随应变硬化指数（n值）增加而增大，其形状会受到塑性应变比（r值）的轻微影响。此外，非二次性屈服方程也被应用于成形极限预测中。Graf和Hosford基于M-K模型，使用Hosford屈服准则预测了双向拉应变状态下的FLC，他们发现增加n值，对r值无影响。近年来，较为复杂的唯象模型[9—10]也被纳入M-K模型框架内预测FLC。

在实验研究方面，成形极限图（Forming limit diagrams，FLD）反映了材料失效前的应变状态，广泛应用于成形过程中的断裂分析和预测。在这方面，有学者做了大量基础而深入的工作。Gensamer[11]用实验评估材料的成形性时加入了局部变形的影响，完善了成形极限图的实验理论。Keeler等[12—13]研究了金属成形特性，建立了双轴拉伸成形区域的成形极限图。Goodwin等[14]采用不同的试验方法，将成形极限曲线扩展到拉-压区，扩大了成形极限图的适用范围。金属成形极限理论逐渐变成了一套成熟的评价体系，成功应用于汽车与航空航天等多项工业领域[15—16]。

在数值仿真方面，刘毅等[17]用DYNAFORM软件模拟得到了150～250 ℃温度范围内AZ31镁合金的FLC，并与试验结果进行对比。刘振勇等[18]采用ABAQUS有限元软件根据改变应变路径法，建立了9种不同宽度的有限元模型，模拟得到5754-H111铝合金的成形极限图，与试验对照后发现有良好的吻合度。江煜煌[19]运用LS-DYNA软件对汽车冲压件的冲压成形及回弹过程进行了数值模拟分析，分析了几项关键因素对成形结果的影响。李磊等[20]通过LS-DYNA软件对金属板料单点渐进成形极限进行了数值模拟，模拟结果与试验一致，能够较好预测渐进成形件的成形极限。

现国内高温合金成形研究较少，且均未考虑合金板材的各向异性。针对GH625高温合金材料，文中首先对0°，45°和90°这3个不同方向的材料进行了拉伸试验，获取了材料的塑性应变比与应变硬化指数等基础力学参数，然后分别基于Swift，Hill以及M-K理论模型预测了GH625的成形极限曲线，接着采用半球胀形试样对一系列不同尺寸的沙漏型试件进行了胀形实验，绘制了GH625的成形极限曲线，并与理论预测结果进行对比，结果表明基于颈缩理论的集中性失稳准则的FLC与试验结果最为吻合，预测结果最好；最后采用数值模拟方法探究了不同摩擦因数及球头直径对GH625材料主应变分布的影响规律，发现摩擦因数为0.01或者球头直径不超过60 mm时，可以获得较为理想的变形模式，有利于改善板料最终的失效位置。

1 基本材料参数测试

1.1 试验准备

研究的镍基高温合金材料牌号为GH625。测试用带材为固溶状态，微观组织由γ相基体与少量的NbC，TiC，M6C碳化物组成。γ相基体晶粒细小，平均晶粒度为9级，尺寸约15.8 μm，NbC平均尺寸约6.9 μm。为了研究该材料的各向异性以及准确获得本构模型中的材料参数，分别进行与挤压方向成0°，45°，90°这3个方向上的单向拉伸试验。试件的设计根据GB 3076—1982，GB 5027，GB 5028—2008的规定要求进行，试件总长度和平行段长度分别为200 mm和90 mm，夹持区宽度为 40 mm，过渡圆弧半径为15 mm，具体尺寸如图1所示。

因轧制板材尺寸为2345 mm×169 mm×0.2 mm，受板材几何尺寸的限制，GH625沿90°方向上的试件尺寸限制为169 mm，两侧夹持端改为24.5 mm，具体尺寸如图1b所示，GH625试件厚度为0.2 mm，不同方向上试件的具体获取方式如图1c所示。

试验设备包括INSTRON5985拉伸试验机和DIC应变测量系统，如图2a所示。试验以3 mm/min的准静态速度对试件进行加载。所有试件均在同一台试验机上进行测试，每种试件进行5次重复试验，以保证测量结果的准确性和可靠性。

1.2 试验结果

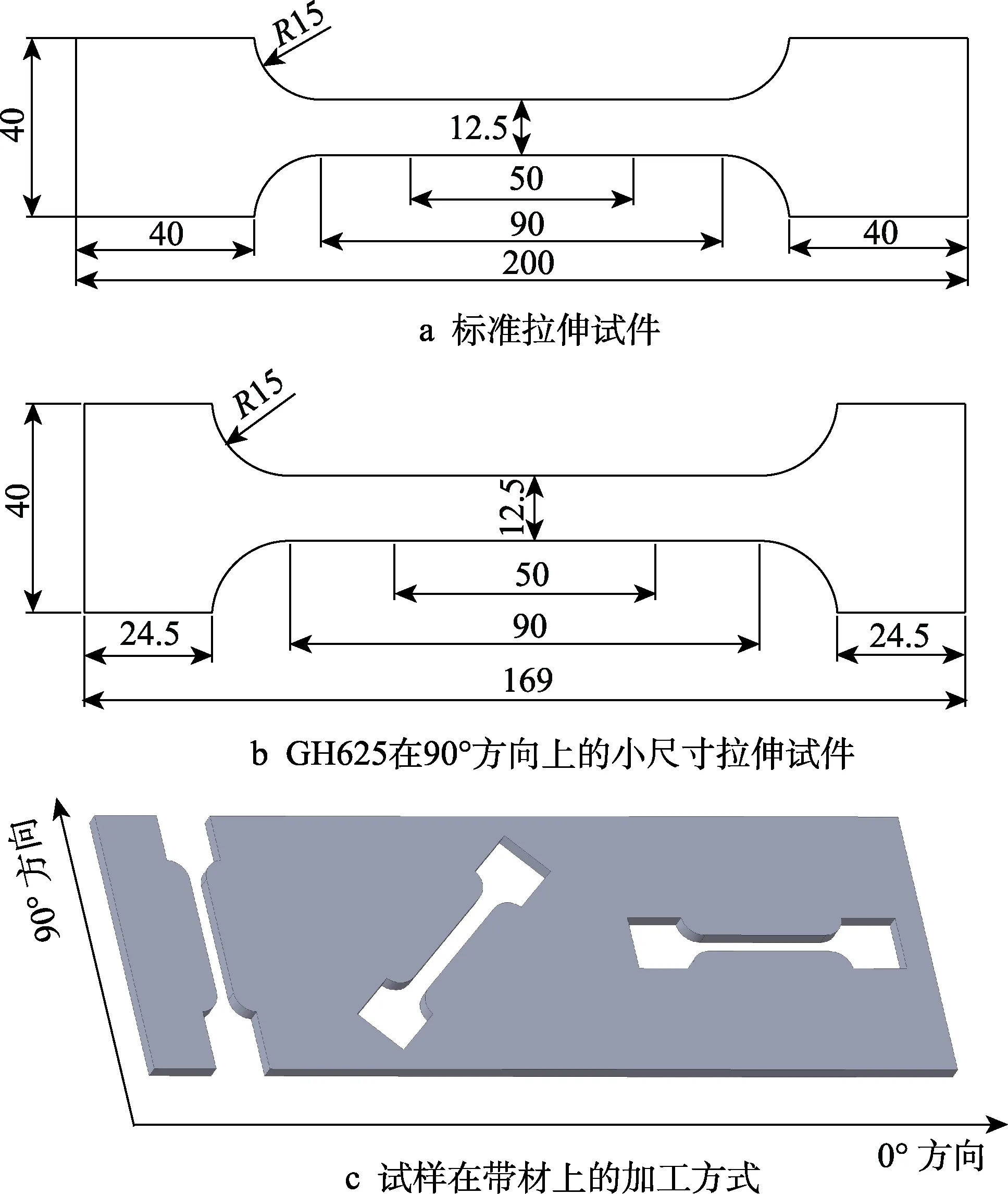
图1 单轴拉伸试验试件Fig.1 Uniaxial tensile test specimens

通过数据处理之后，得到不同方向上的真实应力-真实应变曲线如图2b所示，从曲线上可以看出，GH625材料在塑性硬化阶段不同方向的性能是不同的，沿材料轧制方向的硬化能力强于其余方向，表明该材料具有较为明显的各向异性。

塑性应变比r由试件在单轴拉伸过程中宽度方向应变εw和厚度方向应变εt的比值确定：

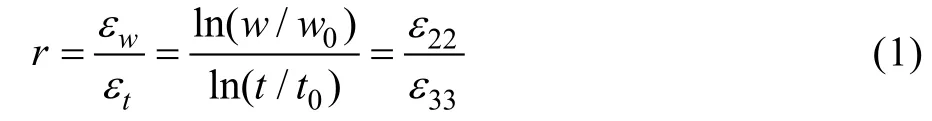
式中：t0，w0分别为试验前试件的厚度和宽度；t和w分别为试验结束后试件的厚度和宽度。

试件在变形过程中厚度方向上的变形信息较难准确获得，根据金属塑性材料在产生塑性变形时符合的体积不变原则，可推导出：

由单轴拉伸试验可得到材料的真实应力-真实应变曲线，根据真实应力-真实应变曲线弹性阶段到均匀塑性变形阶段，参考应变硬化指数的求解方法[21]可计算出材料的n值。

2 成形极限计算

2.1 GH625高温合金FLC理论预测

2.1.1 Swift均质模型

Swift模型将金属材料韧性破坏分为两个阶段，即稳定塑性流动阶段和非稳定塑性流动阶段。第一阶段，因应变强化，需要增大外力试样才能产生持续的塑性变形。第二阶段，材料产生颈缩效应拉力，尽管真实应力增加，但抗拉强度显著降低。根据体积不变原则、各向同性强化模型和Drucker公式，Swift给出分散性失稳准则下的极限应变表达式[22]：

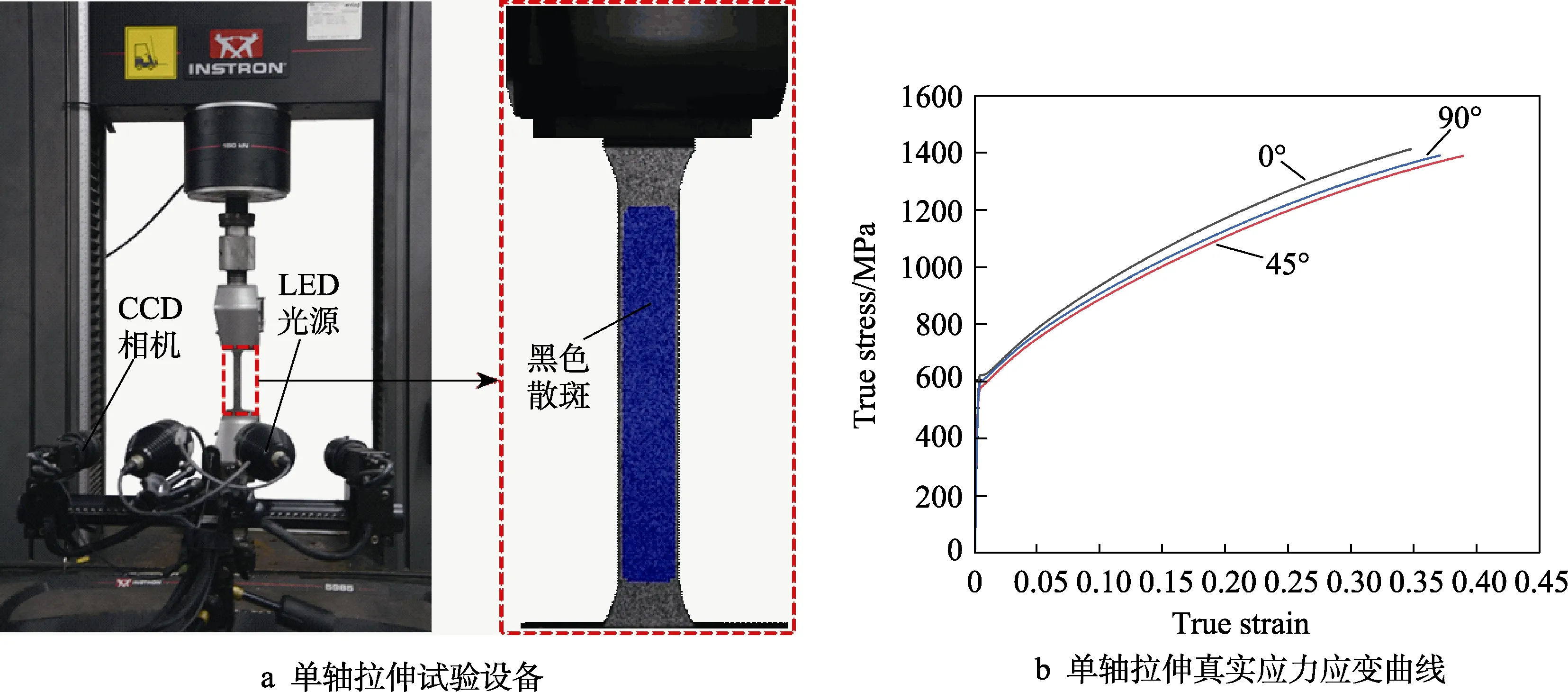
图2 材料参数测试Fig.2 Material parameters testing

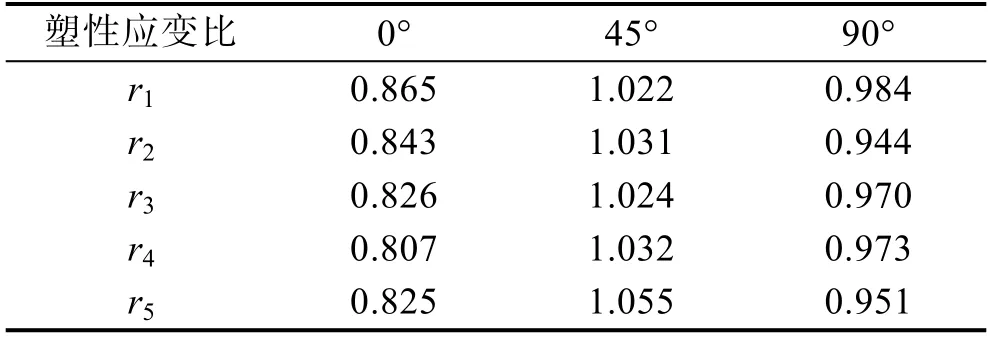
表1 塑性应变比r 值Tab.1 Plastic strain ratio r

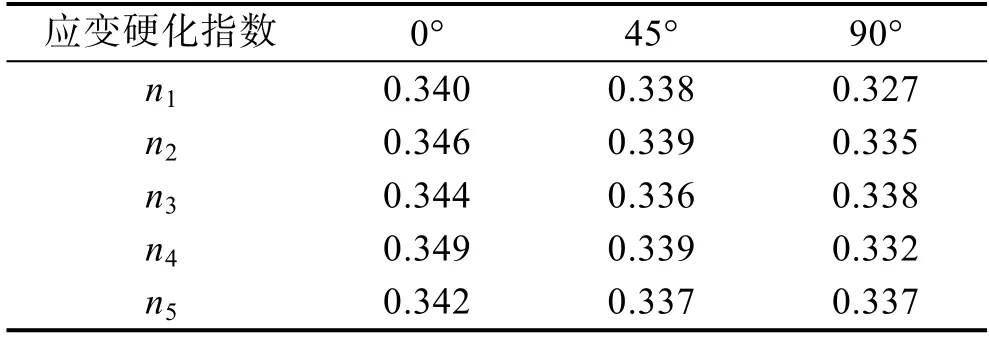
表2 应变硬化指数n 值Tab.2 Strain hardening index n

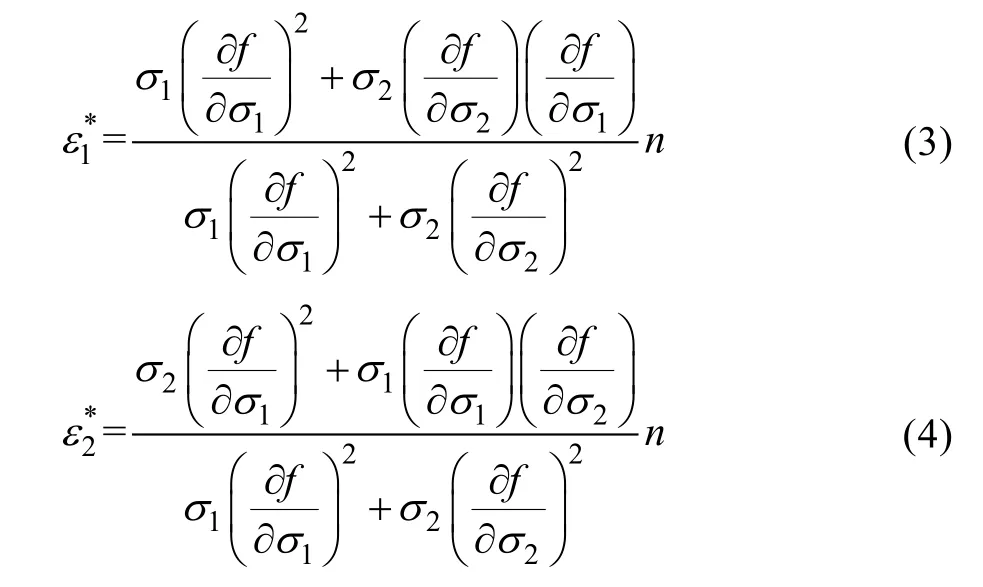
式中：f为由屈服准则计算得到的等效应力；n为硬化系数；σ1和σ2分别为最大主应力和最小主应力。

2.1.2 Hill均质模型

Hill认为在单轴拉伸条件下，局部颈缩发展方向和加载方向重合，因此颈缩区应变只由金属薄板减薄引起，根据张自强[23]推导，基于Hill集中性失稳的成形极限最大主应变和最小主应变可表示为：

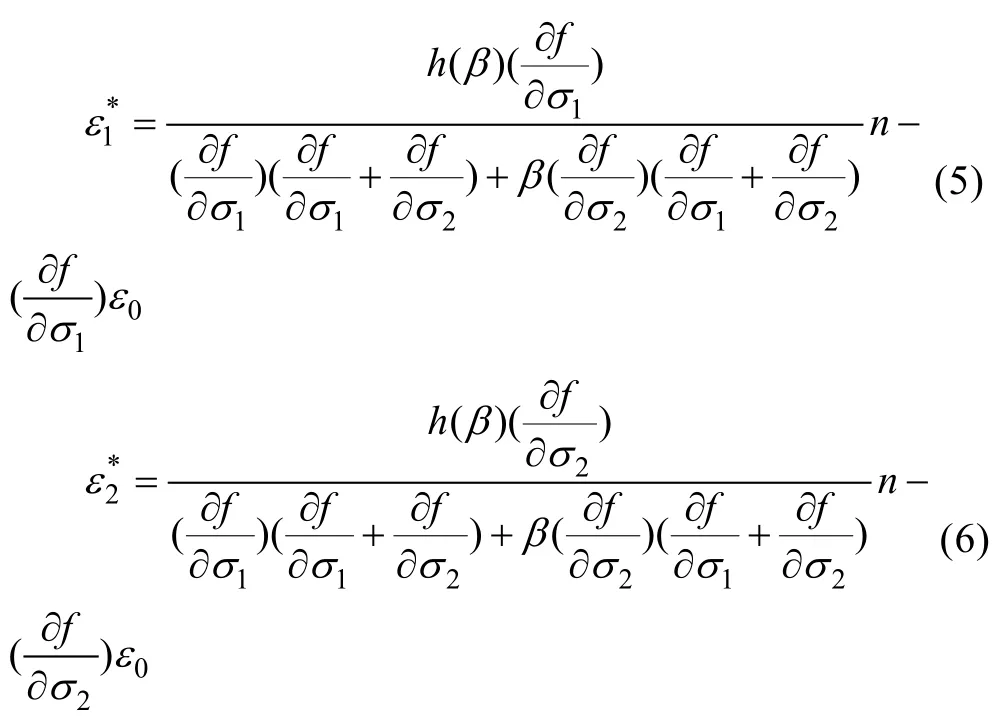
2.1.3 基于M-K模型的FLC计算过程

M-K模型假定金属板材存在初始缺陷，取如图3所示单元体，可分为均匀区A区和非均匀区B区。非均匀区和均匀区存在θ夹角，为便于分析，这里建立两套坐标系x1-x2-x3和xm-xn-x3，两套坐标系可通过旋转矩阵进行转换。

记均匀区施加应变为α，根据Hill48屈服方程：

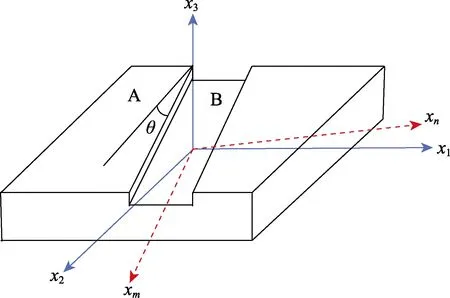
图3 M-K模型计算示意图Fig.3 Schematic diagram of M-K model calculation

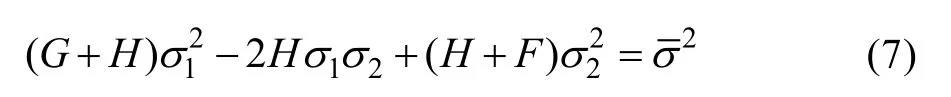
可求出该时刻A区应力比，进而由硬化方程求出A区应力应变信息。文中采用了两种硬化方程，比较不同硬化方程的理论预测效果。Hollonmon硬化方程：

Swift硬化方程：

根据A区和B区静力平衡条件和变形协调条件，可求出非均匀区应变比，继而求解B区等效塑性应变增量，然后对B区应力应变信息更新，最后比较A和B两区等效塑性应变增量比，如比值大于10，则认为达到极限状态，此时最大主应变和最小主应变即为FLC所求值。

2.1.4 理论计算结果

成形极限理论模型所需参数均由上一节单轴拉伸试验获取，Hill模型中F，G，H，N分别为0.4737，0.5455，0.4545，1.5622；Swift模型中Ks，ns，ε0分别为1503.6 MPa，0.273，0.0083；Hollomon模型中Kh，nh分别为1828.785 MPa，0.290。

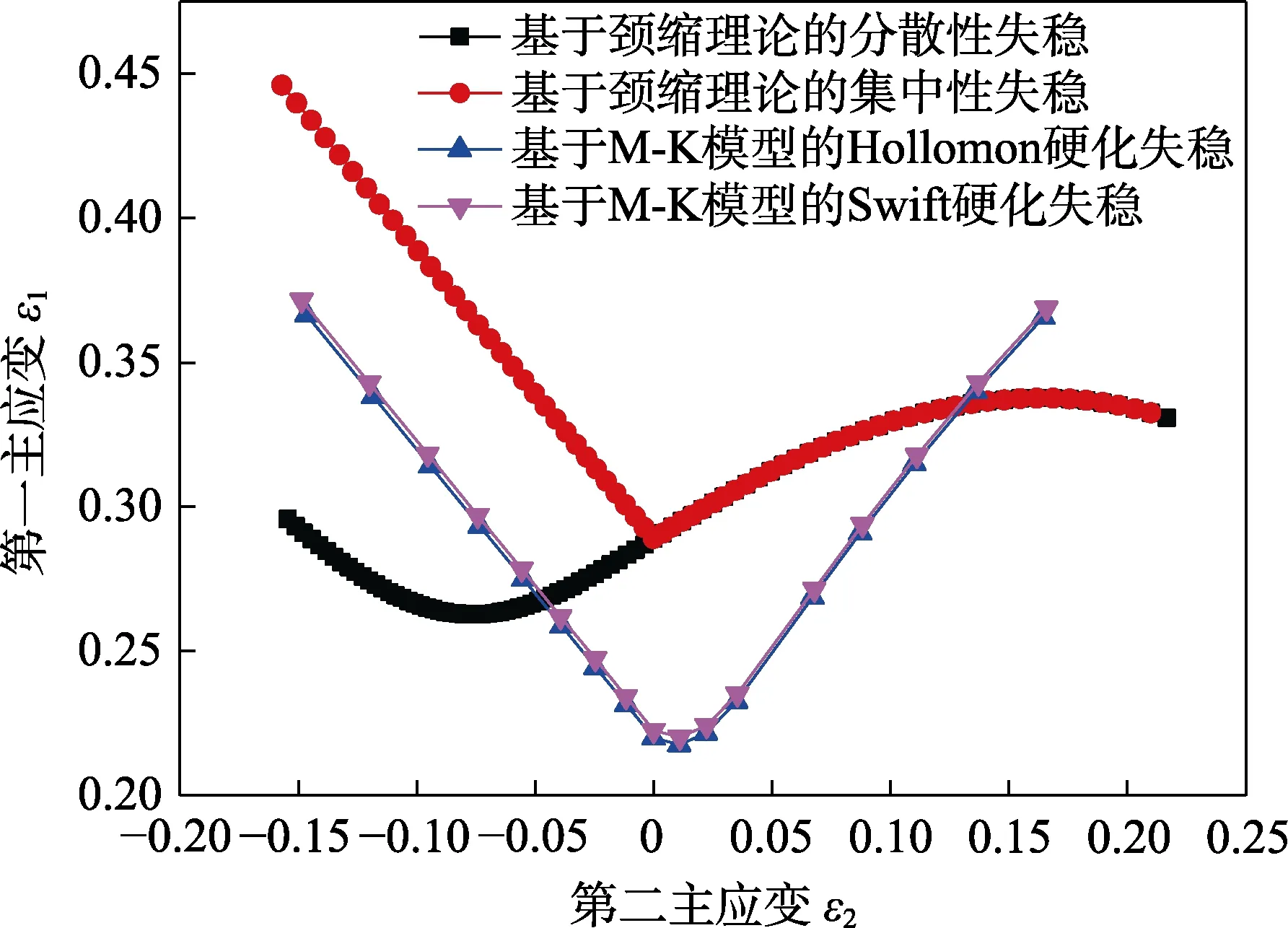
图4 理论预测成形极限Fig.4 Forming limit curves predicted by theoretical calculation

理论预测成形极限图见图4，可以看出，GH625板材受拉压应力状态时，相同第二主应变条件下，基于颈缩理论的集中性失稳理论的第一主应变，比基于M-K模型的预测结果平均约高0.068。笔者分析，其原因主要在于两者假设不同，后者假定板材存在初始缺陷，在外荷载作用下，易产生应力集中，从而降低其极限状态下最大主应力值，故计算结果偏保守；基于颈缩理论的分散性模型和其他3条曲线差异均较大，其原因在于该理论假设了两者主应变方向同时达到极限状态，板材受拉压应变状态时，更容易在拉应为等效塑性应变；变方向失效，压应变方向安全，故导致偏差较大。GH625板材在双向拉应变状态下，基于颈缩理论的两种模型计算结果几乎一致，说明极限状态下两个主应变方向同时失效。基于M-K模型的第一主应变随第二主应变几乎呈现线性增加。第二主应变大于0.125时，极限状态下，基于M-K模型的第一主应变开始高于基于颈缩理论的预测值，笔者认为，基于颈缩理论的模型破坏模式主要受第一主应变控制，故第二主应变介于0.12～0.18之间时，极限状态第一主应变变化较小。上述模型理论计算结果将在下节和试验结果进行比对。

2.2 GH625高温合金FLC试验结果

2.2.1 试样制备

文中采用半球形冲头和圆形模具对不同形状的标准件进行冲压胀形，直至试件发生破裂。8种不同宽径比的胀形试件如图5所示，其中尺寸H代表试件整体长度，L代表平行部分长度，推荐取值25～50 mm，本试验取30 mm，若试验材料强度较低或成形性较差，可根据实际试验情况酌情增加。W为平行部分宽度，R为过渡圆弧半径，当W较窄时，取R=30 mm，当W较宽时，为避免试件在压边圈处断裂，可使用不同曲率的半圆弧切边代替平行部分长度，取R=50 mm。表3详细列出了全部胀型试件的尺寸，其中GH625代表材料类型。本方案所采用的冲压试验装置，所用设备主要包括VIC-3D应变测量系统、成形极限专用夹具、INSTRON 5894万能试验机，加载速度为1 mm/s，由于冲头与试样之间的摩擦会影响破坏机理和应变数据的计算，因此采用0.05 mm厚的聚四氟乙烯（PTFE）薄膜和PTFE润滑剂双重润滑作用来减少摩擦。

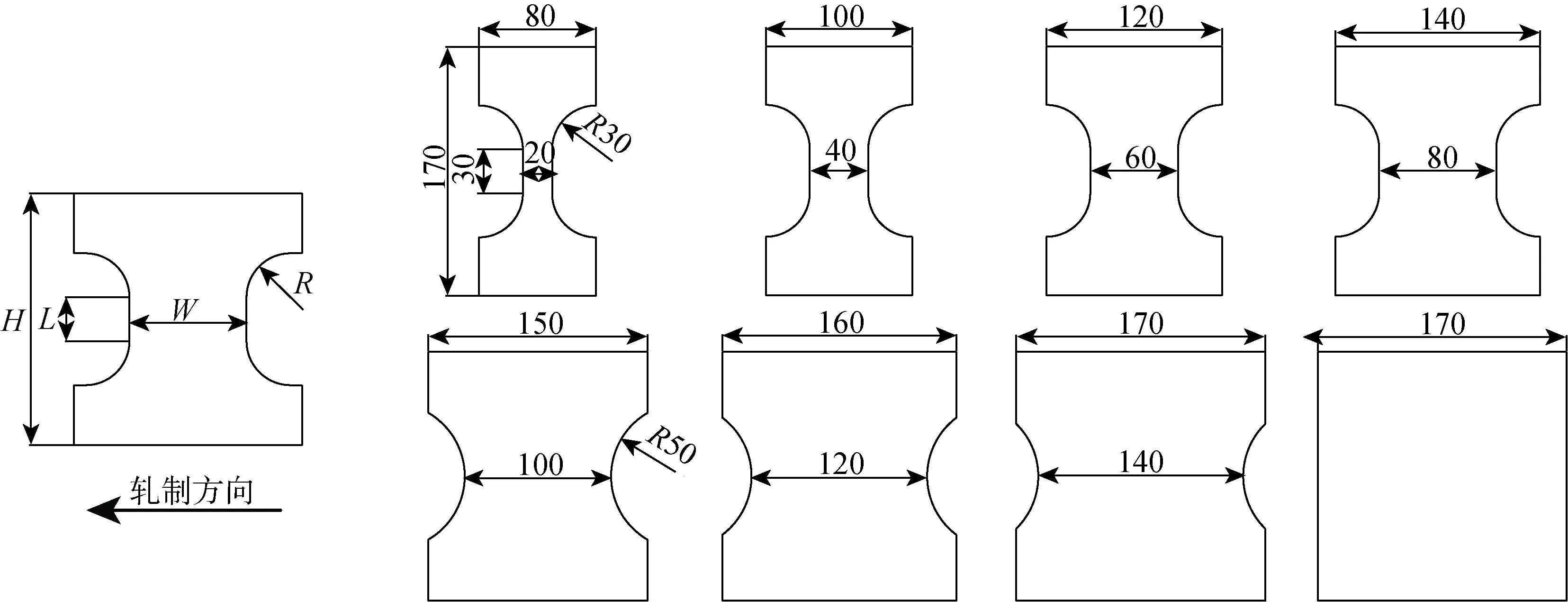
图5 试件尺寸示意图Fig.5 Schematic diagram of specimen sizes

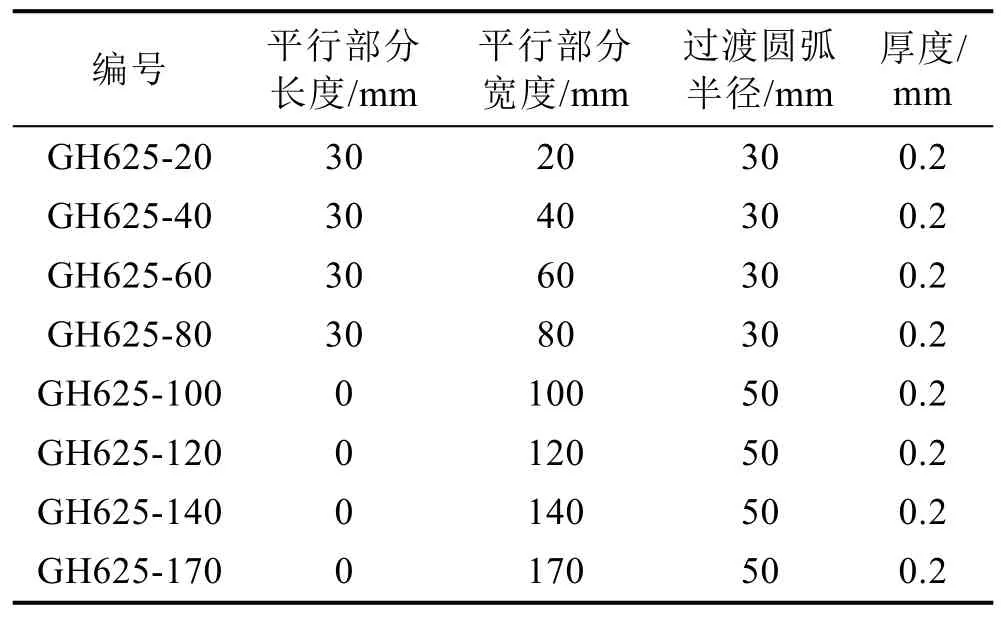
表3 胀型试件尺寸Tab.3 Specimen number

2.2.2 试验结果

图6展示了不同宽度的胀型试件在冲压过程中对应的载荷-位移曲线。可以看出，8种不同尺寸的胀型试件表现出了相似的载荷-位移曲线关系，即随着球头位移的增加，球头表面受到的反力也逐渐增加直至材料失效，载荷出现迅速下降，整个胀型过程中载荷-位移曲线表现出明显的非线性特征。此外，随着胀型试件中间材料宽度的不断增加，其峰值载荷也不断增加。

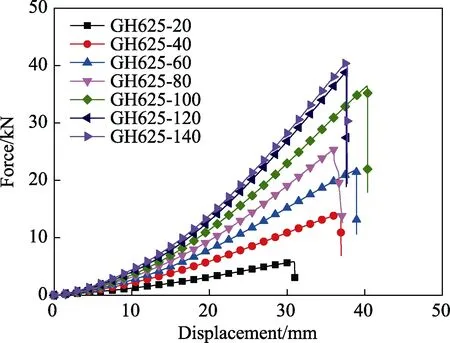
图6 胀型试件的载荷-位移曲线Fig.6 Force-displacement curve of the bulging specimens

图7展示了胀形实验结束后8种试件的失效模式，可以看出，尽管试件宽度不同，试验结束后断口均出现在材料上方，断口方向沿圆周方向分布。由于在实际冲压过程中，球头与试件表面的摩擦作用很难完全消除，尽管试验过程中采用了聚四氟乙烯（PTFE）薄膜和PTFE润滑剂双重润滑作用来减少摩擦，但是球头与试件的摩擦作用依然存在，可能导致了最终的破裂区域偏离中心位置。

图7 试验结束后的失效位置Fig.7 Failure positions of specimens after the experiments

通过VIC系统对胀形试件进行表面应变处理，可以分别获得试件在试验过程中任意时刻的应变结果（包括主应变、次应变和不同应变分量），将主应变用作纵坐标，次应变用作横坐标，提取试件破裂前一刻的表面主次应变，将其数值绘在主次应变坐标系中，即可绘制出 GH625材料的试验成形极限图（FLC），如图8所示。结合理论计算，笔者发现，板材在拉压应力状态下，基于颈缩理论的集中性失稳计算结果和试验结果吻合程度最高，说明该批GH625板材均匀程度较高。基于M-K模型的计算结果因假定了初始缺陷，拉压应变状态下，失效主应变偏低，结果偏保守；双向拉应变状态下，且次应变大于0.13时，极限主应变结果偏高。在拉压应变状态下Swift分散性失稳的预测结果和试验结果差异较大，而双向受拉应变状态预测结果和试验结果较为一致。

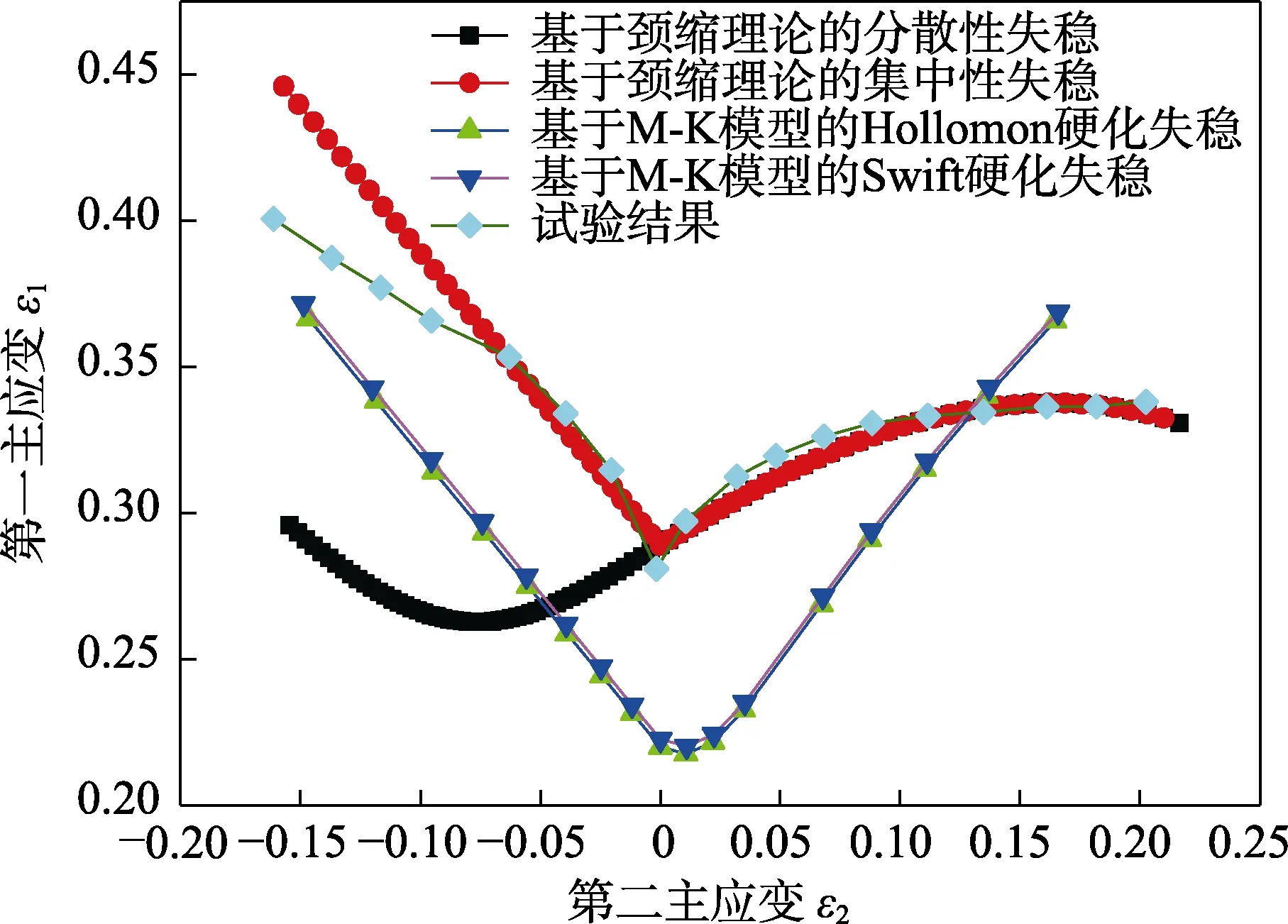
图8 成形极限曲线的实验结果与理论预测结果对比Fig.8 Comparison in FLC between experimental and theoretical results

图9分别展示了GH625-20，GH625-100，GH625-170这3种典型试件在胀形试验过程中的应变比演化过程。可以看出，随着胀形载荷的不断增加，3种试件的应变比分布逐渐向中间位置集中，其中，GH625-20试件中间位置的应变比从初始加载时刻的0演化至破裂前的-0.49，说明该试件主要发生了单向拉伸变形；在破裂前时刻，GH-625试件中间位置的应变比约为0.13，说明其主要发生了双向拉伸变形，由于中间部分仍有部分材料缺少压边筋约束，因此没有形成等双向拉伸变形；而GH625试件由于被压边筋完全约束住且试件宽度远大于球头直径，因此，其中间应变比数值可以达到0.93，等双轴拉伸变形模式较为明显。

3 数值模拟研究

3.1 有限元模型建立

冲压模型在LS-DYNA软件中建立，其中冲头和压板部件为20#刚性材料，考虑到金属板料的各向异性，金属板料为36#（barlat89各向异性材料），材料参数如表1和表2所示。冲头与板料之间设置面面接触算法来模拟其在胀形过程中的接触行为。上下压板与板料之间分别建立面面接触设置，且6个方向的自由度进行完全约束，球头模型采用刚体单元进行模拟，直径为100 mm，除竖直方向外的5个自由度完全约束。为了提高计算效率，在刚性冲头上施加一个沿竖直方向向下的大小为200 mm/s的恒定速度。GH625-170有限元模型如图10所示。

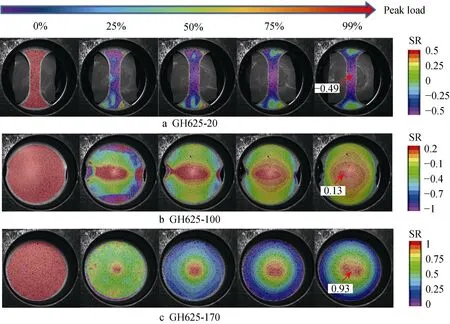
图9 应变比演化云图Fig.9 Strain ratio evolution contour

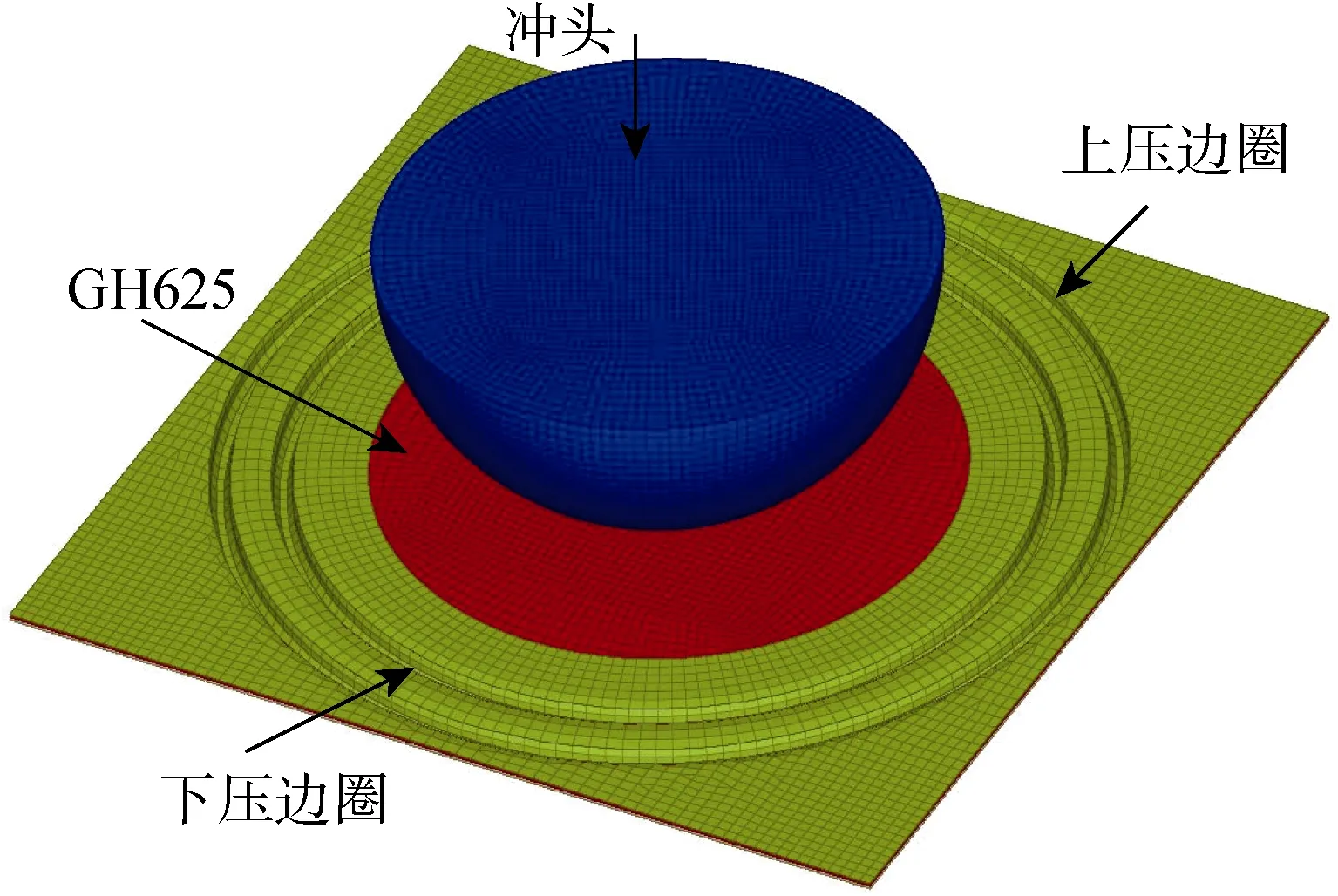
图10 胀形有限元模型Fig.10 Finite element model of stamping test

3.2 有限元模型验证

图11—13分别从变形模式、载荷-位移曲线以及主应变分布这3个方面对比了GH625-170试件的胀形试验结果与仿真结果。从图13可以看出，试验结束后，GH625-170试件压边筋外侧由于材料在胀形过程中流动变形而出现了起皱变形，而压边筋内侧的材料在球头向下移动的过程中不断地向下变形，最终形成了一个向外凸起光滑饱满的半圆形轮廓，仿真模型与试验结果基本吻合，由于本构模型中没有考虑材料的失效行为，因此仿真结果只显示了弹塑性阶段材料的变形模式，同时图14表明数值模拟预测的载荷-位移曲线与试验结果在变化趋势及数值大小方面基本一致。图15对比了材料在成形过程中的主应变分布情况，可以看出，在试件断裂前一刻，在试件中心靠下位置形成了一圈颜色较深的应变集中区域，而试件中心的应变值小于周围的主应变数值，因此在下一刻，试件最终在主应变集中带内出现了破裂，数值模拟预测的失效前一刻材料的主应变分布与试验结果吻合较好。

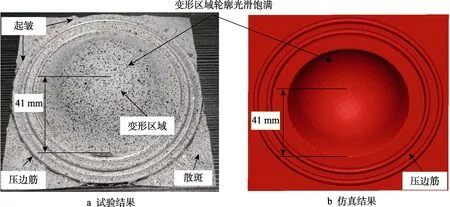
图11 试验和仿真的变形模式对比Fig.11 Comparison in deformation patterns between experimental and numerical results

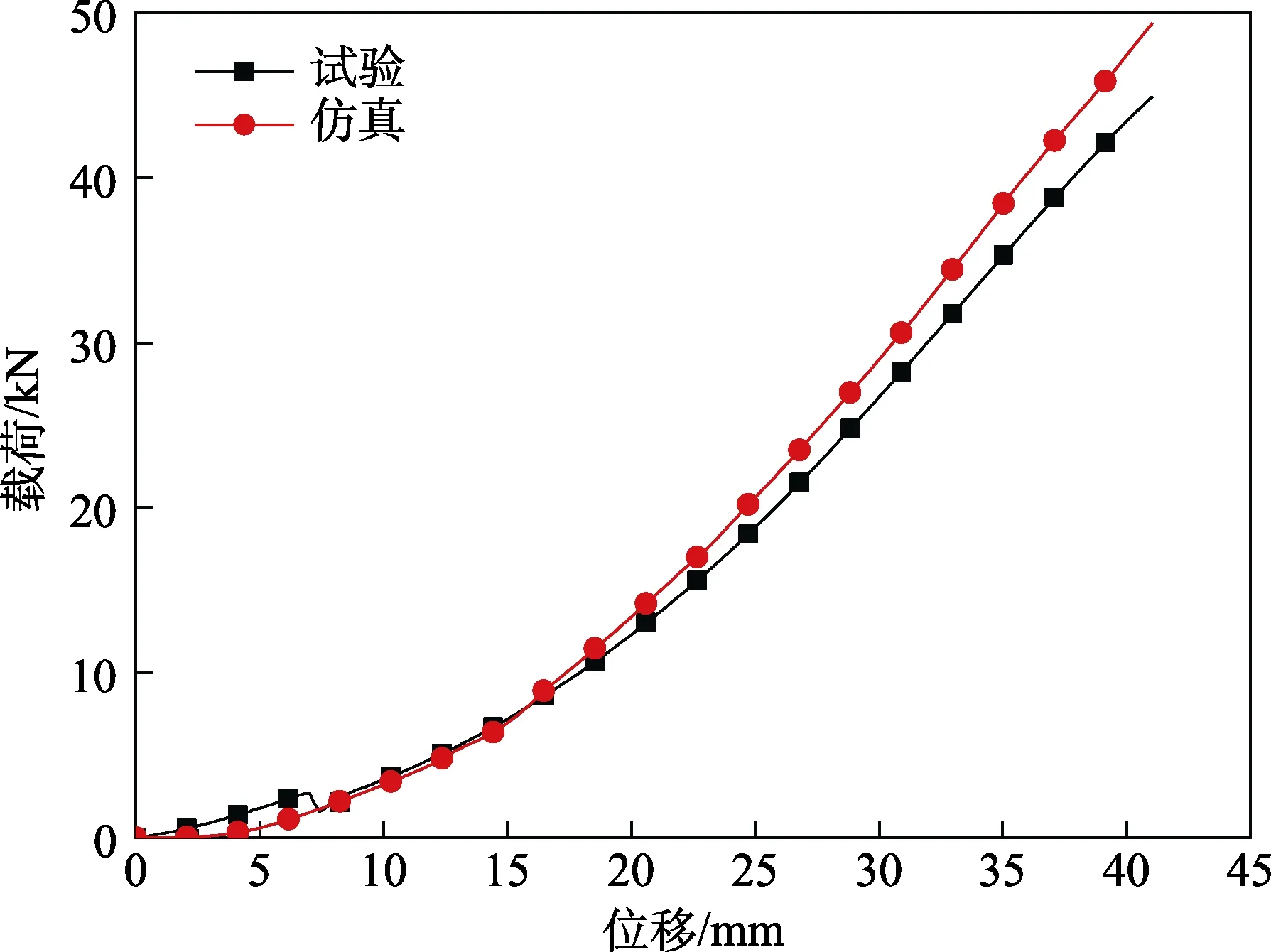
图12 试验和仿真的载荷-位移曲线对比Fig.12 Comparison in load-displacement curve between experimental and numerical results

3.3 摩擦因数及球头直径对成形性能的影响

根据试验结果可以看到，8种试件均没有在试件中间位置断裂，在试验过程中，球头与试件的摩擦因数以及球头的尺寸大小均与试件的变形模式密切相关，而在实际试验中，材料间的摩擦因数往往难以精准控制，球头的加工也将带来成本的增加。有限元技术可以大大降低实验成本且可以高效地研究不同摩擦因数对材料成形性能的影响，因此，在验证后的数值模型的基础上，可以进一步开展关于不同摩擦因数及球头形状对GH625材料成形性能的影响规律。

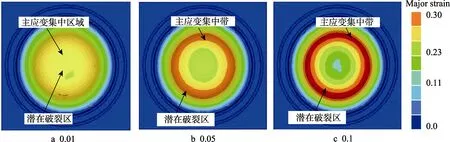
图14 摩擦因数对主应变分布的影响Fig.14 Effects of friction coefficients on the major strain distribution

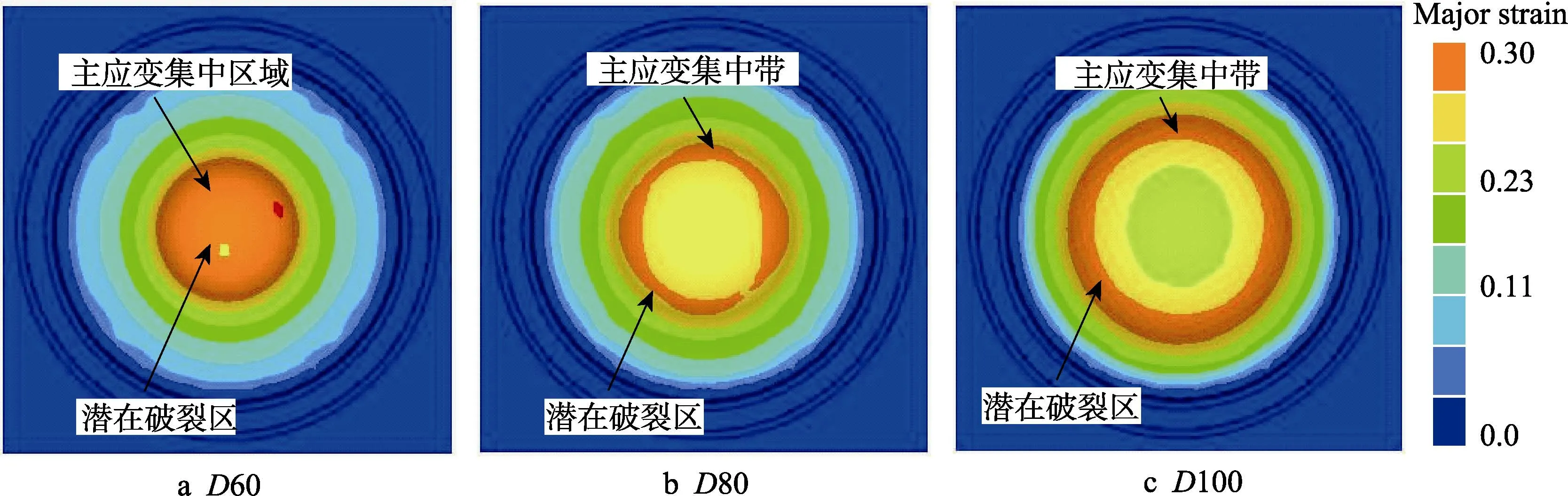
图15 球头直径对主应变分布的影响Fig.15 Effects of diameter of punch on the major strain distribution

图14对比了3种不同摩擦因数（球头与试件之间）对板料主应变分布的影响情况，3种摩擦因数大小分别为0.01，0.05，0.1。可以看出，当球头与试件之间的摩擦因数为0.01时，试件中间位置的材料得到了充分的变形并最终形成了主应变分布较均匀的云图，此时试件的潜在破裂位置较为容易出现在试件中心位置；当摩擦因数等于或者超过0.05时，试件中间位置的材料并不能得到充分变形，在胀形后期，主应变最大值主要集中在偏离试件中心位置靠下的周向区域，此时容易造成材料的最终破坏位置远离试件中心位置。

图15对比了3种不同球头直径对板料主应变分布情况的影响规律，3种球头直径分别为60，80，100 mm。可以发现，当球头直径为60 mm时，试件中心位置的材料最终发生了充分变形，形成了分布均匀的主应变云图，没有在远离中心位置的环向区域形成最大的主应变集中带；而当球头直径超过60 mm后，试件中间位置的材料不能发生充分变形，最终会在偏离中心的位置形成较大主应变集中的环形带，不利于破裂位置形成在中心区域。

4 结论

分别采用理论预测、试验测试以及数值模拟的手段探究了GH625镍基高温合金板料的成形性能，通过应用理论模型对成形极限进行预测，依靠试验手段对预测结果进行验证分析，并结合数值方法进一步深入探索工艺参数对其成形性能的影响规律，可以得到以下3个方面的结论。

1）理论预测结果显示，基于颈缩理论的FLC在双向受拉应力状态结果较为一致，但受拉压应力状态时，集中性失稳模型较为合理，并且和试验结果较为吻合。

2）通过半球胀形实验方法可以建立包含单轴拉伸、双轴拉伸和等双轴拉伸等多样变形模式的板料成形极限图和成形极限曲线。

3）基于各向异性本构模型，在LS-DYNA软件中建立了可靠的数值模型，通过数值模拟方法发现摩擦因数为0.01或者球头直径不超过60 mm时，可以获得较为理想的变形模式，有利于改善板料最终的失效位置。