分析法在空间几何证明中的灵活应用

■四川省绵阳实验高级中学 刘荣燕

分析法和综合法是数学学习中应用较为普遍的相互依赖、相互渗透的思想方法，也是培养同学们分析问题、解决问题等能力的重要的思想方法。分析法和综合法作为数学的思想方法，在数学的各个方面都有重要的应用。

空间几何是高中数学知识体系的重要知识模块之一，也是高考的必考内容。其中几何证明题在空间几何中占有极其重要的位置，为帮助同学们掌握好几何证明题证明的分析方法，现举例说明。

一、由因索果

从已知条件出发，通过定向思维，逐步逼近结论。

例1如图1，在四棱锥A-BCDE 中，CD ⊥平面ABC，BE∥CD，AB=BC=CD，AB⊥BC，M为AD 上一点，EM ⊥平面ACD。

（1）求 证：EM ∥平面ABC；

（2）若CD=2BE=2，求点D 到平面EMC 的距离。

分析：（1）要证明线面平行，可从线线平行和面面平行这两个角度来进行分析、证明；也可结合平面或空间几何体其他平行性质进行证明。（2）熟悉点到面的各种方法，根据题目条件灵活选择、应用。

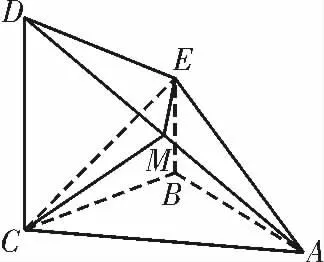
图1

解：（1）如图2，取AC 的中点F，连接BF，因为AB=BC，所以BF⊥AC。

因为CD ⊥平面ABC，所以CD⊥BF。

又因为CD ∩AC=C，所以BF⊥平面ACD。

因为EM ⊥平面ACD，所以EM∥BF。

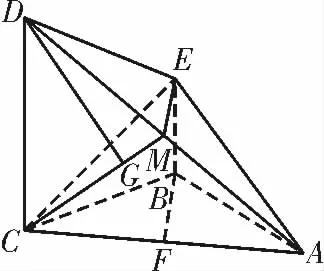
图2

（2）因为EM ⊥平面ACD，EM ⊂面EMC，所以平面CME⊥平面ACD。

因为平面CME∩平面ACD=CM，过点D 作DG⊥CM 于G，如图2，则DG⊥平面CME，DG 的长即为点D 到平面EMC 的距离。

由已 知CD ⊥平 面ABC，BE ∥CD，AB=BC=CD=2BE，可得AE=DE。

又EM ⊥AD，所以M 为AD 的中点。

总结：（1）构造不同的线面垂直，再根据垂直于同一平面的两直线互相平行，得出线面平行，再由线面平行的判定定理得出结论；（2）解答时，证明问题务必要依据判定定理，因此线面的平行问题一定要在所给的平面中找出一条直线与这个平面外的直线平行；（3）叙述时一定要交代面外的线和面内的线，这是许多同学容易忽视的问题，也是高考试卷中最容易扣分的地方，因此在表达时一定要引起注意。

二、由果索因

从结论出发，进行逆向推理，找出要证明的条件。

例2如图3，在四棱锥P-ABCD 中，平面PAD⊥平面ABCD，底面ABCD 为直角梯形，BC∥AD，∠ADC=90°，BC=CD=为线段AD 的中点，过BE 的平面与线段PD，PC 分别交于点G，F。

（1）求证：GF⊥PA。

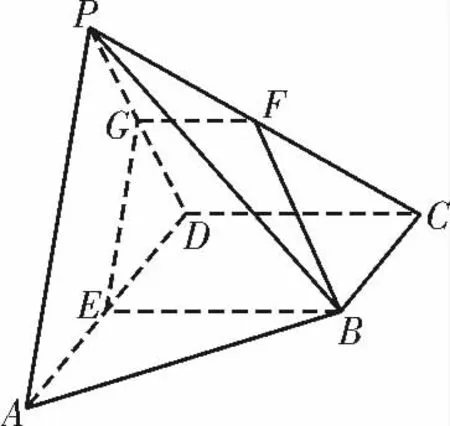
图3

分析：（1）从问题出发，要证明线线垂直，在空间几何中主要采用线面垂直来证明，但该问题中两条直线没有直接的线线垂直条件，因此还需要通过相关条件进行适当的转化。（2）存在类问题，一般是采取假设该问题成立，然后把它当成已知条件来分析，最后得出结果；如果存在，作答时，只需倒过来进行书写即可。

解：（1）因为且E 为线段AD 的中点，所以BC=DE。

又BC∥AD，所以四边形BCDE 为平行四边形，所以BE∥CD。

又平面BEGF∩平面PCD=GF，所以BE∥GF。

又因为∠ADC=90°，所以AD⊥CD。

又CD∥BE，所以BE⊥AD。

又平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，所以BE⊥平面PAD。

又PA⊂平面PAD，所以BE⊥PA。

又因为BE∥GF，所以GF⊥PA。

（2）存在点G，且G 为DP 上靠近D 点的三等分点。证明如下：

因为PA=PD，E 为线段AD 的中点，所以PE⊥AD。

又平面PAD⊥平面ABCD，所以PE⊥平面ABCD，所以PE⊥EB。

又因为AD ⊥EB，所以以E 为坐标原点，EA，EB，EP 所在直线为x 轴，y 轴，z轴，建立如图4 所示的空间直角坐标系E-xyz。

又E 为线段AD 的中点，所以PE=1，则P（0，0，1），B（0，1，0），E（0，0，0），D（-1，0，0），所 以

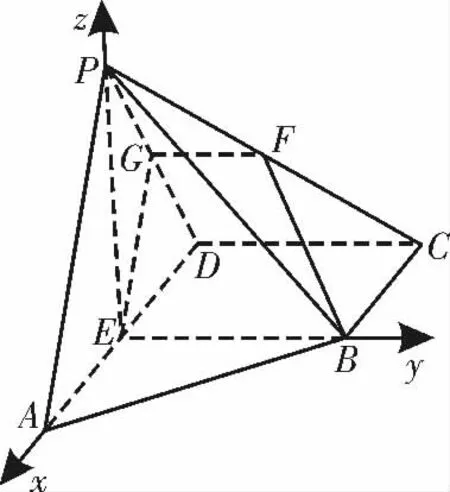
图4

总结：（1）利用线面平行的判定定理与性质定理证得线线平行，再利用线面垂直的判定定理证得线面垂直，从而得到线线垂直。（2）用空间向量方法求线面角，需建立适当的空间直角坐标系，数形结合，将几何问题转化为代数问题求解，考查同学们的运算能力与空间想象能力。

三、由因索果与由果索因的综合推理

根据已知条件和求证的结论进行综合推理。

例3如图5，正三棱柱ABC-A1B1C1的高为，其底面边长为2。已知M，N 分别是棱A1C1，AC 的中点，D 是棱CC1上靠近C 的三等分点。求证：

（1）B1M∥平面A1BN；

（2）AD⊥平面A1BN。

图5

分析：（1）根据题目本身的一些平行和垂直条件，再从问题出发，结合图形，我们分析出该题可由线线平行来证明线面平行；（2）要证明线面垂直可从线线垂直和面面垂直这两种途径进行分析。

解：（1）连接MN，在正三棱柱ABCA1B1C1中，AA1∥CC1且AA1=CC1，则四边形AA1C1C 是平行四边形。

因为M，N 分别是棱A1C1，AC 的中点，所以MN∥AA1且MN=AA1。

又因为在正三棱柱ABC-A1B1C1中，AA1∥BB1且AA1=BB1，所以MN∥BB1且MN=BB1，所以四边形MNBB1是平行四边形，所以B1M∥BN。

又B1M平 面A1BN，BN ⊂平 面A1BN，所以B1M∥平面A1BN。

（2）在正三棱柱ABC-A1B1C1中，AA1⊥平面ABC，BN⊂平面ABC，所以BN⊥AA1。

在正△ABC 中，N 是AB 的中点，所以BN⊥AC。

又AA1，AC⊂平面AA1C1C，AA1∩AC=A，所以BN⊥平面AA1C1C。

又AD⊂平面AA1C1C，所以AD⊥BN。

由题意，AA1=，AC=2，所以AN=

又因为∠A1AN =∠ACD=90°，所以△A1AN∽△ACD，则∠AA1N=∠CAD。

所以∠ANA1+ ∠CAD = ∠ANA1+∠AA1N=90°，则AD⊥A1N。

又BN ∩A1N =N，BN，A1N ⊂平 面A1BN，所以AD⊥平面A1BN。

总结：（1）根据平行四边形性质得线线平行，再根据线面平行判定定理得结论。（2）根据平面几何知识得线线垂直，再根据线面垂直性质定理得线线垂直，最后根据线面垂直判定定理得线面垂直。（3）空间几何垂直、平行关系证明中应用转化与化归思想的常见类型：①要证明线面、面面平行，只需转化为证明线线平行；②要证明线面垂直，只需转化为证明线线垂直；③要证明线线垂直，只需转化为证明线面垂直。