立体几何中平行和垂直问题的证明
■江苏省华罗庚中学 李普红
平行与垂直关系的证明是高考考查立体几何的高频考点,大部分问题都可以用传统的几何方法解决,有一部分问题需要建立空间直角坐标系利用空间向量解决。用传统法解题时,应注重线线平行、线线垂直、线面平行、线面垂直、面面平行、面面垂直等问题的性质定理和判定定理的灵活应用。用向量法解题时,应建立恰当的空间直角坐标系,准确表示各点与相关向量的坐标。
考向一:证明线面平行
例1如图1,已知空间几何体BACDE 中,△BCD与△CDE 均是边长为2的等边三角形,△ABC 是腰长为3,底边为BC 的等腰三角形,平面CDE⊥平面BCD,平面ABC⊥平面BCD。
(1)试在平面BCD 内作一条直线,使得直线上任意一点F 与E 的连线EF 均与平面ABC 平行,并给出证明;
(2)求三棱锥E-ABC 的体积。

图1
解析:(1)如图2 所示,取DC 的中点为N,BD 的中点为M,连接 MN,则MN 即为所求。
连接EM,EN,取BC的中点H,连接AH。
因为△ABC 是腰长为3的等腰三角形,H 为BC 的中点,所以AH ⊥BC。
又平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,AH ⊂平面ABC,所以AH⊥平面BCD。
同理可证EN⊥平面BCD。
所以EN∥AH。
又M,N 分别为BD,DC 的中点,所以MN∥BC。
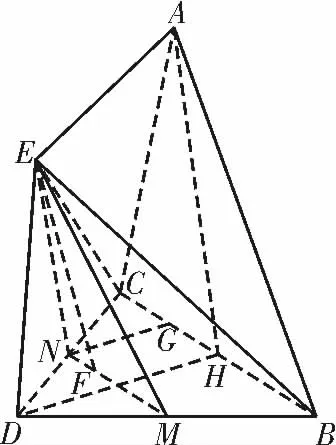
图2
又MN∩EN=N,MN⊂平面EMN,EN⊂平面EMN,所以平面EMN∥平面ABC。
又EF ⊂平面EMN,所以EF ∥平面ABC,即直线MN 上任意一点F 与E 的连线EF 均与平面ABC 平行。
(2)连接DH,取CH 的中点为G,连接NG,则NG∥DH。
由(1)可知EN∥平面ABC,所以点E 到平面ABC 的距离与点N 到平面ABC 的距离相等。
又△BCD 是边长为2的等边三角形,所以DH ⊥BC。
又平面ABC⊥平面BCD,平面ABC∩平面BCD =BC,DH ⊂平面BCD,所以DH ⊥平面ABC,所以NG⊥平面ABC。
考向二:证明面面平行
例2如图3,在长方体 ABCD-A1B1C1D1中,AB=1,AD=2,E,F分别为AD,AA1的中点,Q 是BC 上一个动点,且BQ=λQC(λ>0)。
(1)当λ=1 时,求证:平面BEF∥平面A1DQ。
(2)试问:是否存在λ,使得BD⊥FQ? 若存在,请求出λ 的值;若不存在,请说明理由。
解析:(1)当λ=1 时,Q 为BC 的中点,因为E 是AD 的中点,所以ED=BQ。
又ED∥BQ,则四边形BEDQ 是平行四边形,所以BE∥QD。

图3
因为E,F 分别是AD,A1A 的中点,所以EF∥A1D。
因为BE∩EF=E,EF⊂平面BEF,BE⊂平面BEF,所以平面BEF∥平面A1DQ。
(2)如图4,连接AQ,BD,FQ。
因为 A1A ⊥平面ABCD,BD ⊂ 平面ABCD,所以A1A⊥BD。
若 BD ⊥FQ,又A1A,FQ⊂平面A1AQ,且A1A ∩FQ=F,所以BD⊥平面A1AQ。
因为AQ⊂平面A1AQ,所以AQ⊥BD。
在矩 形ABCD 中,由AQ ⊥BD,得△AQB∽△DBA,则所以AB2=AD·BQ。
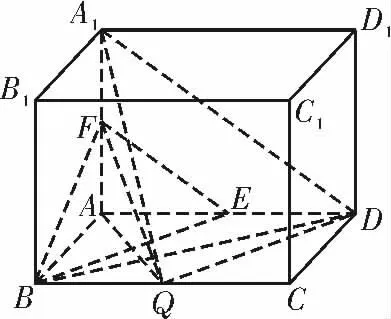
图4
考向三:证明线面垂直
例3如图5,在四棱锥P-ABCD 中,四边形ABCD 为正方形,PA⊥平面ABCD,PA=AB,M 是PC 上一点,且BM⊥PC。
(1)求证:PC⊥平面MBD;
(2)求直线PB 与平面MBD 所成角的正弦值。
解析:(1)连接AC,由PA⊥平面ABCD,BD⊂平面ABCD,得BD⊥PA。
又BD⊥AC,PA∩AC=A,所以BD⊥平面PAC。
又PC⊂平面PAC,则PC⊥BD。
又PC⊥BM,BD∩BM=B,所以PC⊥平面MBD。
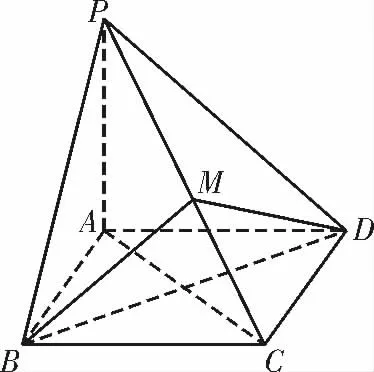
图5
(2)由(1)知PC ⊥平面 MBD,则∠PBM 是直线PB 与平面MBD 所成角。
易证PB ⊥BC,而BM ⊥PC,不妨设PA=1,则BC=1,
考向四:证明面面垂直
例4如图6,在四棱锥 P-ABCD 中,底面ABCD 为菱形,∠ABC=60°,PA⊥平面ABCD,E,M 分别是BC,PD 的中点,直线EM 与平面PAD 所成角的正弦值为,点F 在PC 上移动。
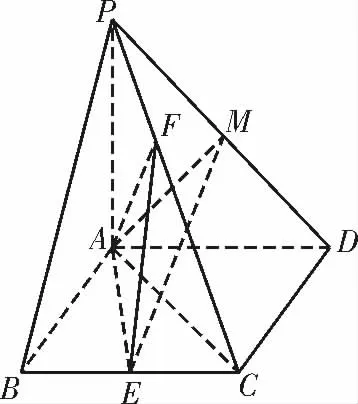
图6
(1)证明:无论点F 在PC 上如何移动,都有平面AEF⊥平面PAD;
(2)当F 恰为PC 的中点时,求二面角C-AF-E 的余弦值。
解析:(1)连接AC,因为底面ABCD 为菱形,∠ABC=60°,所以△ABC 是正三角形。
因为E 是BC 的中点,所以AE⊥BC。
又AD∥BC,所以AE⊥AD。
因为PA ⊥平 面ABCD,AE ⊂平 面ABCD,所以PA⊥AE。
又PA∩AD=A,所以AE⊥平面PAD。
又AE⊂平面AEF,所以平面AEF⊥平面PAD。
由此可证明:无论点F 在PC 上如何移动,都有平面AEF⊥平面PAD。
(2)由(1)得AE,AD,AP 两两垂直,则以A 为坐标原点,AE,AD,AP 所在直线为x 轴,y 轴,z 轴,建立如图7所示的空间直角坐标系A-xyz。
因为AE⊥平面PAD,所以∠AME 是EM 与平面PAD 所成的角。
又AD=AB=2a,设PA=2b,则M(0,a,b),所以AM=从而b=a,所 以PA =AD =2a,则A (0,0,0),B(a,-a,0),C(a,a,0),D(0,2a,0),P(0,0,2a)
平行或垂直关系的证明常出现在解答题的第一问,对同学们的直观想象能力要求很高。特别地,有一类问题是只有在第一问利用几何法证明了垂直关系,才能在后面的问题中建立空间直角坐标系解题,所以平时应注重这方面的训练。

