立体几何解答题科学备考新方向

■四川省绵阳实验高级中学 余 强

从近几年的高考命题情况分析，利用空间向量处理立体几何问题仍是高考命题的热点。通常在第（1）问考查直线与平面、平面与平面平行或垂直的判定；第（2）问考查线面角与二面角的求解，向量法是较好的解题方法，特别是在处理探索性问题时，向量法更具优势。在2021年的复习备考中，特别要注意判定定理与性质定理中条件的完整性，这是解答题解题规范的基本要求。同时要掌握并会运用向量法求解空间角和距离问题，一是要特别重视坐标系的建立，建系的原则是简洁清晰，便于表示相关点的坐标；二是要加强运算能力的训练，熟练、准确的运算是完成解答题的基本要求。历年来立体几何的考查内容比较稳定，但由于在题型、试题材料背景、重要知识点的考法上具有较大的灵活性，近几年立体几何试题在命题设计与立意上不断创新。下面结合部分最新模拟题介绍立体几何试题变化的新趋势，供同学们复习时参考。

方向1:特殊几何体中的位置关系与空间角的求解

我们在平时的学习中碰到很多的立体几何解答题，主要是以棱柱或者棱锥为载体进行考查，而近几年高考是以圆锥为载体考查了线面垂直的位置关系和二面角的计算。解决这类问题，需要我们对于一些特殊几何体（如圆柱、圆锥、正四面体等）的相关性质有深刻的认识，在平时复习中需要我们关注。

例1（河南省中原名校联盟2020—2021 学年高三第一次质检）如图1，S 为圆锥的顶点，O 为底面圆心，点A，B 在底面圆周上，且∠AOB=60°，C，D 分别为SB，OB 的中点。

（1）求证：AC⊥OB；

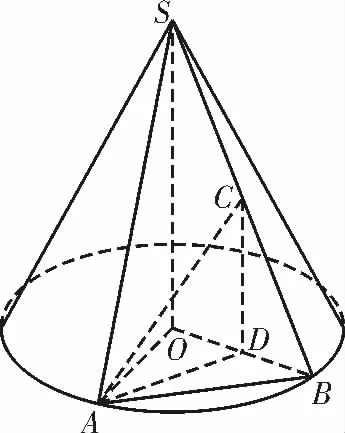
图1

（2）若圆锥的底面半径为2，高为4，求直线AC 与平面SOA 所成的角的正弦值。

解析：（1）由题意知SO⊥底面圆O，C，D分别为SB，OB 的中点，所以CD∥SO，CD⊥底面圆O。

因为OB 在底面圆O 内，所以OB⊥CD。

因为∠AOB=60°，所以△AOB 为正三角形。

又因为D 为OB 的中点，所以OB⊥AD。

又AD∩CD=D，且AD ⊂平面ACD，CD⊂平面ACD，所以OB⊥平面ACD。

又因为AC ⊂平面ACD，所以AC⊥OB。

（2）如图2，以D 为坐标原 点，DA，DB，DC 所在直线为x 轴，y 轴，z轴，建立空间直角坐标系D-xyz，由题意可知A（，0，0），C（0，0，2），O（0，-1，0），S（0，-1，4），故0，2）

图2

评注：解答本题需要同学们熟悉圆锥的定义和性质：以直角三角形的直角边所在直线为旋转轴，其余两边旋转360 度而成的曲面所围成的几何体叫作圆锥，旋转轴叫作圆锥的轴，垂直于轴的边旋转而成的曲面叫作圆锥的底面。

方向2:空间角的探索性和最值问题

立体几何中的存在性问题主要包括两类：一类是与空间平行、垂直等位置关系有关的存在性问题；另一类是与空间角有关的存在性问题。向量法是解决此类问题的常用方法，它可以将几何存在问题转化为代数方程是否有解等问题。

例2（湖南省百校联考2020—2021 学年高三上学期月考）如图3，已知AC⊥BC，DB⊥平面ABC，EA⊥平面ABC，过点D 且垂直于DB 的平面α 与平面BCD的交线为l，AC=BD=1，AE=2。

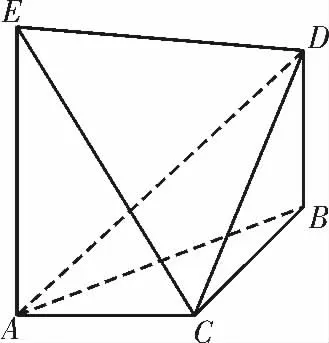
图3

（1）证明：l⊥平面AEC；

（2）设P 是l 上任意一点，求平面PAE与平面ACD 所成锐二面角的最小值。

解析：（1）因为BD⊥α，BD⊥平面ABC，所以α∥平面ABC。

又α∩平面BCD=l，平面ABC∩平面BCD=BC，所以BC∥l。

因为EA⊥平面ABC，所以BC⊥AE。

又BC⊥AC，AE∩EA=A，所以BC⊥平面AEC，从而l⊥平面AEC。

（2）以C 为坐标原点，CB，CA 所在直线为x 轴，y 轴，过C 与AE平行的直线为z 轴，建立如图4所示的空间直角坐标系C-xyz，由题意可知A（0，1，0），C（0，0，0），D（，0，1），E（0，1，2）。设P（a，0，1），则

图4

设平面PAE 的法向量为m=（x1，y1，z1），则得y1=a，z1=0，即m=（1，a，0）。

设平面ACD 的法向量为n=（x2，y2，z2），则令x2=1，得

评注：探索性问题的求解策略：①条件追溯型。一般是先假设结论成立，然后把该结论作为一个已知条件，再结合题目中的其他已知条件逆推，一步一步推出所要求的条件，此时要注意推理的可逆性，不要默认所有的条件都是充要条件。例如，涉及线段上点的位置的探索性问题，一般是先根据条件猜测点的位置再给出证明，所求点大多为中点或三等分点，也可以根据相似的知识找点，求解时注意三点共线条件的应用。②存在探索型。首先假定题中的数学对象存在（或结论成立），然后在这个前提下进行逻辑推理，若由此导出矛盾，则否定假设；否则，给出肯定结论。例如，借助空间直角坐标系，把几何对象上动态点的坐标用参数（变量）表示出来，将几何对象坐标化，这样根据所要满足的题设要求得到相应的方程或方程组，若方程或方程组有满足题设要求的解，则通过参数的值反过来确定几何对象的位置；若方程或方程组没有满足题设要求的解，则表示满足题设要求的几何对象不存在。

方向3:折叠问题

折叠问题是高考立体几何问题中的常客，按照某种要求把一个平面图形折起，转化为空间图形，进而研究图形在位置关系和数量关系上的变化，这就是折叠问题。解决折叠问题时，要注意折叠前后的变量与不变量，折叠前后同一半平面内的数量关系与位置关系均不发生变化。

例3（卓越联盟2020—2021 学年新高考省份高三检测）如图5所示，在直角梯形ABCD 中，AB ∥CD，∠BAD =90°，DC=2AB，AD =AB，E 为BC 的中点，连接DE，将△DEC 沿着DE 翻折成图6 所示的四棱锥C-ABED，使得AB。

图5

图6

（1）证明：平面CDE⊥平面ABED。

（2）求二面角D-BC-A 的余弦值。

解析：（1）在Rt△ABD 中，由AD =AB，可得

在直角梯形ABCD 中，可得BC=CD=2AB，所以△BCD 为等边三角形。

又因为E 为BC 的中点，可得DE⊥BC，所以CE⊥DE。

又因 为DE ∩BE=E，BE，DE ⊂平 面ABED，所以CE⊥平面ABED。

因为CE⊂平面CDE，所以平面CDE⊥平面ABED。

（2）由（1）可知CE⊥EB，DE⊥BE，CE⊥DE，所以以E 为坐标原点，ED，EB，EC 所在直线为x 轴，y 轴，z 轴，建 立 如图7所示的空间直角坐标系E-xyz。

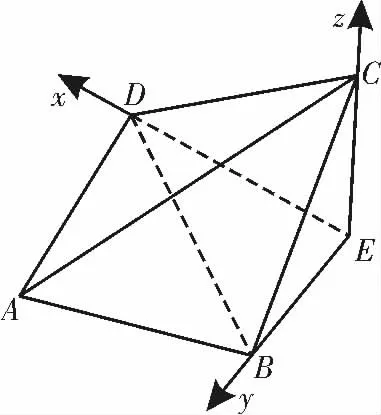
图7

设平面ABC 的法向 量 为n=（x1，y1，z1），由令得即n=（-1，

设平面BCD 的法向量为m=（x2，y2，z2），由令z2=得即

评注：解决翻折问题的核心在于抓住两个图形的特征关系，并弄清翻折前后哪些量发生了变化，哪些量没有发生变化。准确把握平面图形翻折前后的两个“不变关系”：与折痕垂直的线段，翻折前后垂直关系不改变；与折痕平行的线段，翻折前后平行关系不改变。一般情况下，折痕同一侧的量保持着原有的数量关系和线线关系，抓住这些不变量和不变关系是解决翻折问题的关键。不变的线线关系（尤其是图形中线线平行、线线垂直关系）是研究空间位置关系的重要依据；不变的数量关系是求解几何体的数字特征的基础。例如，空间几何体的表面积、体积、空间角、距离、长度等。根据不变量和不变关系，利用有关定理、公式进行推理和计算，从而解决问题，同时注意转化与化归思想在此类问题中的应用。

从近几年的高考数学试题可以看出，立体几何的考题依然坚守“重视通性通法，淡化技巧”，这为我们的备考指明了一个明确的方向：高考数学备考不宜过难过偏，要多从归纳解题通法的角度去进行备考。每年高考数学试卷中的立体几何解答题都主要采用“论证与计算”相结合的模式，即先利用定义、定理、公理等证明空间的线线、线面、面面平行或垂直，再利用空间向量进行空间角的计算，重在考查逻辑推理能力及计算能力。同学们想要掌握立体几何的解题思路，就要立足“奠基、形象、图解、取巧”四个方面进行训练，只有在实战训练中养成逻辑清晰的思路，才能在高考中“扣核心，抓重点，费时少”，达到高效解题的目的。