立体几何中的探索性问题

■甘肃省嘉峪关市第一中学 卢会玉

立体几何解答题的基本模式是论证推理与计算相结合，以某个几何体为依托，分步设问，逐层加深。大部分问题都需要用向量工具解决，处理问题的原则是建模、建系。建模即需要将问题转化为平行模型、垂直模型、平面化模型及角度、距离等的计算模型；建系是依托于题中的垂直条件，建立空间直角坐标系，再利用空间向量求解。探索性问题的类型较多，但一般都是需要探索某边上是否存在某点且满足某种关系，可采用先假设存在某点，再利用对应关系求解的办法解决问题。常见的考查类型如下：

考向一:探索位置问题

例1如图1，在四棱锥P-ABCD 中，PA ⊥ 平面 ABCD，∠ABC= ∠BAD =90°，AD=AP=4，AB=BC=2，M 为PC 的中点。

（1）求异面直线AP，BM 所成角的余弦值；

（2）点N 在线段AD上，且AN=λ，若直线MN 与平面PBC 所成角的正弦值为求λ 的值。

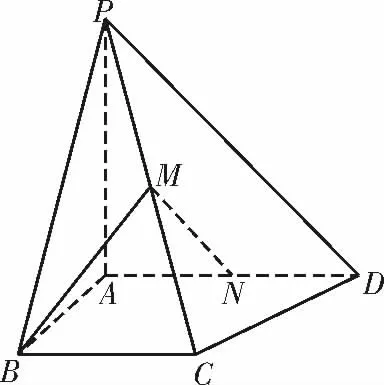
图1

分析：（1）先根据题意建立空间直角坐标系，求得的坐标，再利用线线角的向量方法求解；（2）由AN=λ，设N（0，λ，0）（0≤λ≤4），则=（-1，λ-1，-2），再求得平面PBC 的一个法向量，利用直线MN与平面PBC 所成角的正弦值为再结合求解。

解：（1）因为PA⊥平面ABCD，且AB，AD ⊂平 面ABCD，所 以PA ⊥AB，PA ⊥AD。又因为∠BAD=90°，所以AP，AB，AD 两两垂直，则以A 为坐标原点，AB，AD，AP 所在直线为x轴，y 轴，z 轴，建立如图2 所示的空间直角坐标系A-xyz，由AD=2AB=2BC=4，PA=4，可得A（0，0，0），B（2，0，0），C（2，2，0），D（0，4，0），P（0，0，4）。

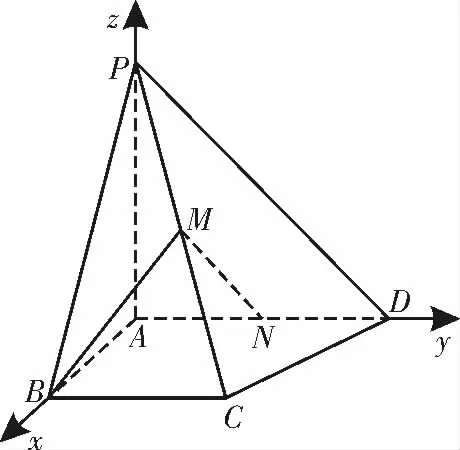
图2

（2）因为AN=λ，所以N（0，λ，0）（0≤λ≤4），则

考向二:探索线线垂直问题

例2如图3，在三棱锥 P-ABC 中，PB⊥平面ABC，AB⊥BC，AB=PB=2，BC=2，E，G 分 别为PC，PA 的中点。

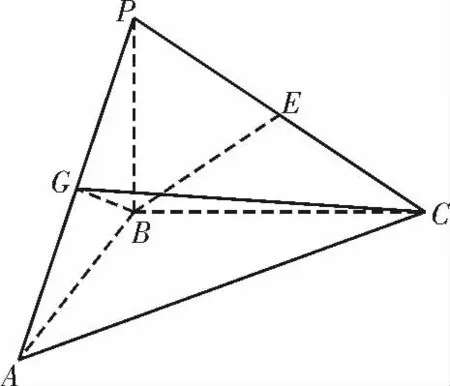
图3

（1）求证：平面BCG⊥平面PAC；

（3）在（2）的条件下，求直线BE 与平面PBN 所成角的正弦值。

分析：（1）由BC⊥PA，BG⊥PA，得PA⊥平面BCG，即可得证；（2）由N 为线段AC上一点，利用向量可设λ，0），得λ，-2），再由PN ⊥BE 可确定λ 的取值；（3）求出平面PBN 的法向量n=（x，y，z），然后利用即可求解。

解：（1）因为PB⊥平面ABC，BC⊂平面ABC，所以PB ⊥BC。又AB ⊥BC，AB ∩BP=B，所以BC⊥平面PAB。又PA⊂平面PAB，则BC ⊥PA。又AB=PB=2，△PAB 为等腰直角三角形，G 为斜边PA 的中点，所以BG⊥PA。又BG∩BC=B，所以PA⊥平面BCG。因为PA⊂平面PAC，则平面BCG⊥平面PAC。

（2）以B 为坐标原点，BA，BC，BP 所在直线为x轴，y 轴，z 轴，建立如图4 所示的空间直角坐标系B-xyz，则B（0，0，0），A（2，0，0），C（0，2，0），P（0，0，2），E（0，，1），则设由PN ⊥即6λ-2=0，得λ=因此

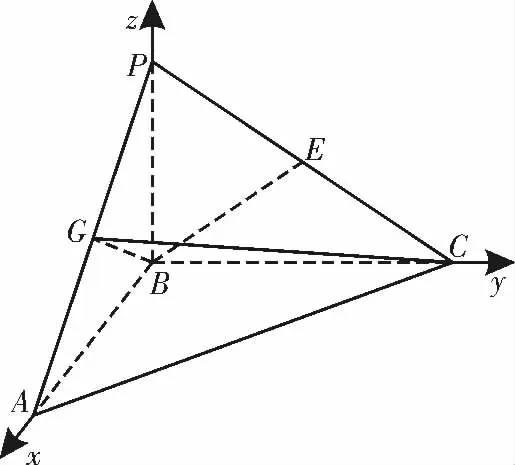
图4

考向三:探索面面垂直问题

例3如图5，在长方体ABCD-A1B1C1D1中，AB=BC=2，E，F 分别为棱AB，B1C1上的点，AE=2EB，C1F=2FB1。

（1）求证：EF ∥平面AA1C1C。

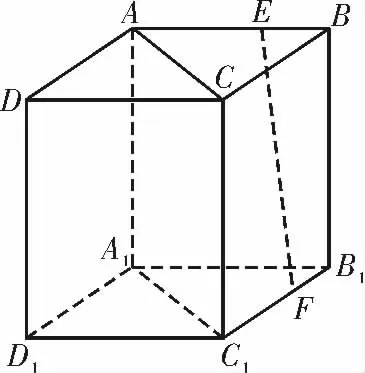
图5

（2）试问：在线段AC 上是否存在一点G，使面EFG ⊥面AA1C1C? 若存在，求出AG 的长；若不存在，请说明理由。

分析：（1）以A1为坐标原点，A1D1，A1B1，A1A 所在直线为x 轴，y 轴，z 轴，建立空间直角坐标系。根据向量的坐标可得由此可证EF∥平面AA1C1C。也可利用直线 EF 与平面AA1C1C 的法向量垂直来证明EF ∥平面AA1C1C。（2）将问题转化为线段AC 上是否存在一点G，使EG⊥AC，则问题不难求解。

解：（1）如图6 所示，以A1为坐标原点，A1D1，A1B1，A1A 所 在直线为x 轴，y 轴，z 轴，建立空间直角坐标系A1-xyz，则A1（0，0，0），B1（0，2，0），C1（2，2，0）。设A（0，0，a），则所以

图6

（2）线段AC 上存在一点G，使面EFG⊥面AA1C1C。

考向四:探索二面角问题

例4如图7，底面四边形ABCD 是边长为3 的正方形，平面ADEF⊥平面ABCD，AF ∥DE，AD ⊥DE，，DE=3。

（1）求直线CA 与平面BEF 所成角的正弦值。

（2）在线段AF 上是否存在点M，使得二面角M-BE-D 的大小为60°? 若存在，求出的值；若不存在，请说明理由。

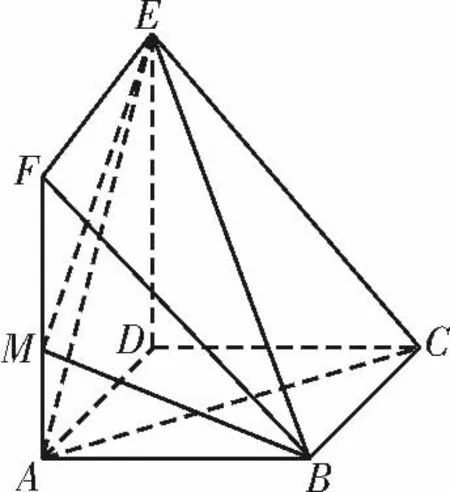
图7

分析：（1）以D 为坐标原点，DA，DC，DE 所在直线为x 轴，y 轴，z 轴，建立空间坐标系，求出平面BEF 的法向量，结合空间向量线面角公式即可求解；（2）设M（3，0，t），，求出平面MBE 的法向量，利用是平面BED 的一个法向量，结合空间向量二面角公式即可求解。

解：（1）因为DA，DC，DE 两两垂直，所以以D为坐标原点，DA，DC，DE所在直线 为x 轴，y 轴，z轴，建立空间直角坐标系D-xyz，如图8 所示，则A（3，0，0），F（3，0，2），

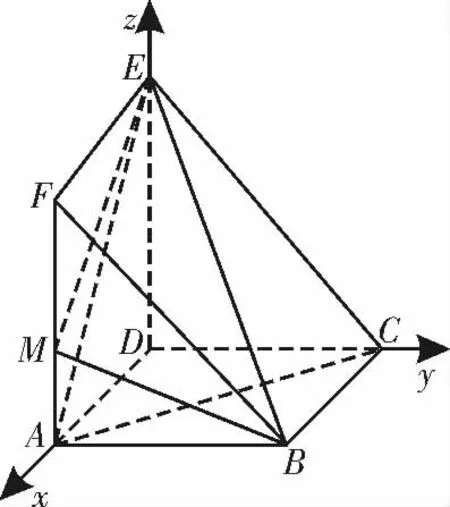
图8

设平面BEF 的法向量为n=（x1，y1，z1），则令为平面BEF的一个法向量。

（2）假设线段AF 上存在点M 满足条件，则可设M（3，0，t），0≤t≤2，则

设平面MBE 的法向量为m=（x2，y2，z2），则令y2=t，可得m=（3-t，t，3）为平面MBE的一个法向量。

故在线段AF 上存在点M，使得二面角M-BE-D 的大小为60°，此时

立体几何这部分内容在高考中的考查情况总体上比较稳定，因此，复习备考时往往有“纲”可循，有“题”可依。在平时的学习中，要加强“一题两法（几何法与向量法）”及识图训练。要求能利用关键点或线的位置，将局部空间问题转化为平面问题；能依托题中的垂直条件，建立适当的空间直角坐标系，将几何问题转化为代数问题。