创新视角下的立体几何最值问题
■江苏省锡山高级中学 包东妹
立体几何是高中数学的重要知识模块之一,历年来的全国高考卷在解答题中必考查一道立几题,常规的考查方式是第一问考查平行或垂直的证明,多为用综合法直接证明,第二问求线线角、线面角或面面角,可以通过建系用空间向量求解,也可以用综合法求解,属中档题。2020 年的全国新高考卷(供山东、海南等地使用)考查了立体几何中的最值问题,体现了立体几何命题的一个趋向,值得重视。本文对立体几何中这类求最值问题的创新题进行解析,为2021届高三数学立体几何备考提供一个参考。
创新1:知识交汇处的立几最值问题,注重综合所以AD∥平面PBC。
又因为AD ⊂平面PAD,平面PAD ∩平面PBC=l,所以AD∥l。
在四棱锥P-ABCD 中,因为底面ABCD是正方形,所以AD⊥DC,所以l⊥DC。
因为PD ⊥平面ABCD,所以AD ⊥PD,所以l⊥PD。
因为CD∩PD=D,所以l⊥平面PDC。
在函数、三角、数列、解析几何等章节中,经常会遇到求最大、最小值的计算问题,我们最常用的方法就是建立目标函数,利用图像、单调性、导数、不等式等工具进行求解。而立体几何中“点”的运动常常使得角的大小、距离的长短等出现“不确定性”,从而产生了最值问题,考点出现在几何和代数的交汇处,提示我们要注重知识间的综合和相互转化,化空间为平面,搭建沟通几何与代数的桥梁。
例1(2020 年 新 高考全国Ⅰ卷)如图1,四棱锥P-ABCD 的底面为正方形,PD ⊥底面ABCD。设平面PAD 与平面PBC的交线为l。
(1)证明:l ⊥平面PDC;
(2)已知PD=AD=1,Q 为l上的点,求PB 与平面QCD 所成角的正弦值的最大值。
解析:(1)在正方形ABCD 中,AD∥BC。

图1
(2)如图2,建立空间直角坐标系D-xyz。
因为PD=AD=1,所 以D (0,0,0),C(0,1,0),A(1,0,0),P(0,0,1),B(1,1,0)。
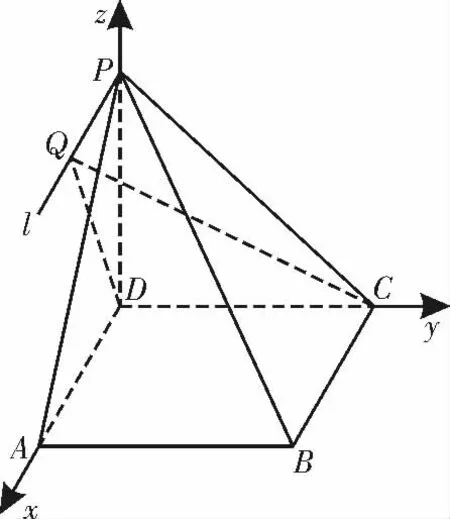
图2
设直线PB 与平面QCD 所成角为θ,根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线PB 与平面QCD 所成角的正弦值当且仅当m=1时取等号。
点评:本题涉及的知识点有线面平行的判定和性质,线面垂直的判定和性质,利用空间向量求线面角,利用基本不等式求最值,也可以对根号下的部分构造函数求导求最值,这是将几何与代数进行融合的一类题型,求解策略是建立目标函数,利用函数思想或不等式的方法求解。
创新2:数学文化背景下的立几最值问题,注重情境
数学文化是指数学的思想、精神、方法、观点、语言,以及数学的概念和思想方法在形成和发展中所体现的文化特征与文化价值。教育部考试中心下发《关于2017年普通高考考试大纲修订内容的通知》,增加了数学文化的要求,明确提出在高考数学考题中要体现数学文化。近几年的全国高考命题及各地模拟卷,在这方面做了一些积极的探索,出现了一些经典试题。归纳发现,数学文化主要考查我国古代优秀数学成果和数学史的内容,通过命题渗透数学史、数学美和数学理性精神,提高人文素养,传承民族精神,树立同学们的民族自信心和自豪感。
例2(2020 年山东青岛模拟)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵;底面为矩形,一侧棱垂直于底面的四棱锥称为阳马;四个面均为直角三角形的四面体称为鳖臑。如图3,在堑堵ABC-A1B1C1中,AB⊥AC。
(1) 求证: 四棱锥B-A1ACC1为阳马;
(2)若C1C=BC=2,当鳖臑C1-ABC 的体积最大时,求锐二面角C-A1B-C1的余弦值。
解析:(1)因为A1A⊥底面ABC,AB⊂面ABC,所以A1A⊥AB。
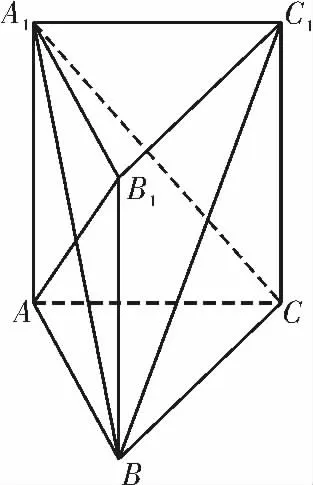
图3
又AB⊥AC,A1A∩AC=A,所以AB⊥面ACC1A1。
又四边形ACC1A1为矩形,所以四棱锥B-A1ACC1为阳马。
(2)因为AB⊥AC,BC=2,所以AB2+AC2=4。
又因为A1A⊥底面ABC,所以VC1-ABC=当且仅当AB=AC=时,VC1-ABC取得最大值
因为AB⊥AC,A1A⊥底面ABC,所以以A 为坐标原点,AB,AC,AA1所在直线为x 轴,y轴,z 轴,建立如图4 所示的空间直角坐标系A-xyz。
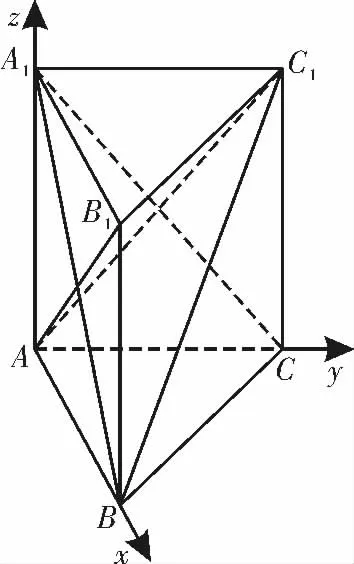
图4
设平面A1BC 的一个法向量为n1=(x1,y1,z1),由
令z1=1,得所以平面A1BC的一个法向量为
设平面A1BC1的一个法向量为n2=(x2,y2,z2),同理可得
点评:本题以中国古代发明和创造为素材,结合数学知识和原理编拟试题,体现古代劳动人民的智慧和成果。突破此类试题的关键是读懂题意,理解文化背景中的堑堵、阳马、鳖臑其实是长方体的一部分或可以由它变形得到,从而进一步抽象出空间位置关系。涉及体积的最值位置的寻找倒是不困难,利用不等式可以迅速找到,从而第(2)问是在“静态”下求解角的大小,属于常规问题。
创新3:动态生成下的立几最值问题,注重联系
除了“点”的运动会产生“不确定性”,图形的翻折、拼接、旋转等也会改变空间点、线、面的位置关系,从而形成动态生成下的立体几何最值问题,解决此类问题,需要关注运动前和运动后的变量和不变量,注重前后联系。
例3(2020年山东德州模拟)如图5,在边长为2的正方形ABEF 中,D,C 分别为EF,AF 上的点,且ED=CF,现沿DC 把△CDF 剪切,拼接成如图6 所示的图形,再将△BEC,△CDF,△ABD 沿BC,CD,BD折起,使E,F,A 三点重合于点A′,如图7。
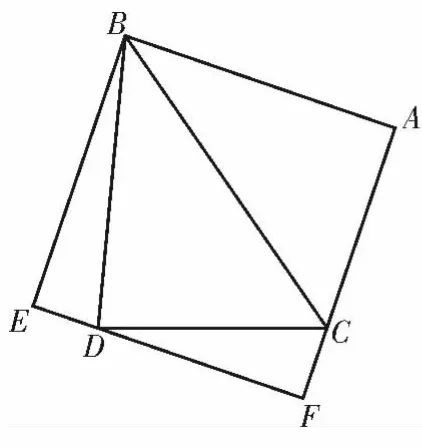
图5
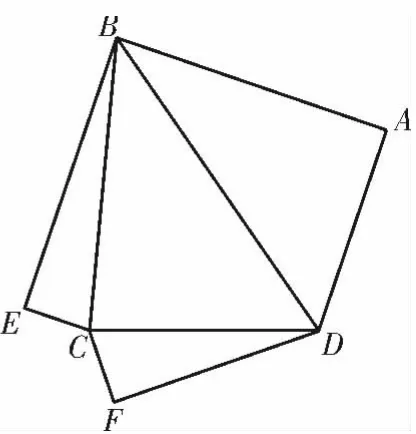
图6
(1)求证:BA′⊥CD;
(2) 求二面角B-CD-A′最小时的余弦值。
解析:(1)折叠前BE⊥EC,BA ⊥AD,折叠后BA′⊥A′C,BA′⊥A′D,又A′C∩A′D=A′,所以BA′⊥平面A′CD,所以BA′⊥CD。
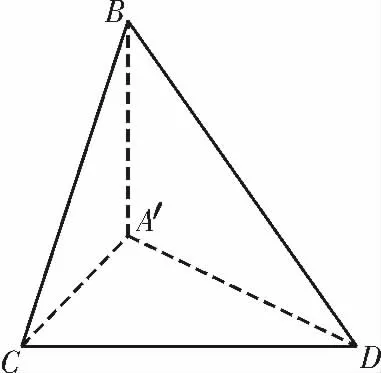
图7
(2)由(1)及题意知A′C⊥A′D,因此以A′为原点,A′C,A′D,A′B所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系,如图8所示。
令A′C=a,A′D=b,则a+b=2,C(a,0,0),D(0,b,0),B(0,0,2)。
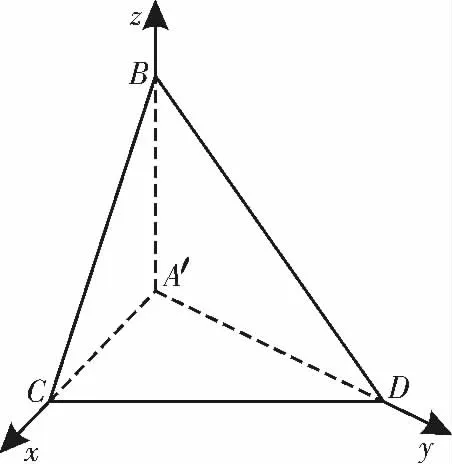
图8
点评:此题是一个由平面到空间的翻折、拼接问题,求解此题的关键有三个:①注意折叠前后的变量和不变量。这里折叠前后的三个直角是不变的,得到空间中的三个线线垂直关系,为第二问建立空间直角坐标系埋下伏笔;变化的是翻折前ED 的长度,导致了拼接后A′C,A′D 的不确定,而A′C 和A′D 的和又是不变的。②注意拼接的顺序。这里将△CDF 中C 和D 的顺序进行了交换。③利用不等式求最值是一个难点。用好a+b=2这个条件,将4 代换成(a+b)2是构造出一次倒数型的关键。总而言之,要顺利求解此类问题,必须要关注翻折前后的联系,关注交叉知识之间的联系。
立体几何是高考高频考点,通过问题的解决,可以提升同学们的直观想象、数学抽象和逻辑推理等素养。而立体几何的最值问题,又将几何和代数糅合在一起,考查同学们将几何问题代数化的能力,遇到复杂的数学文化情境或翻折、拼接等动态生成的最值问题,要耐心审题,大胆转化,细心求解。

