巧解抛物线中的面积之比问题
浙江省衢州第二中学(324000) 万祺
在解析几何解题过程当中,学生往往存在一系列困难,比如对平面解析几何的基本思想理解不到位;代数恒等变形、运算操作能力弱等.本文将针对一类与三角形面积之比有关的考题进行探究,此类问题往往运算的结构不对称,运算难度较大.下面拟从一个问题入手,建立适当模型,探寻合理的解决方案,力求有所突破.
1 建立模型
例1如图1,已知抛物线L:y2=4x 的焦点为F,过点M(5,0)的动直线l 与抛物线L交于A,B 两点,直线AF 交抛物线L 于另一点C.记ΔABC,ΔCFM 的面积分别为S1,S2,求的最小值.
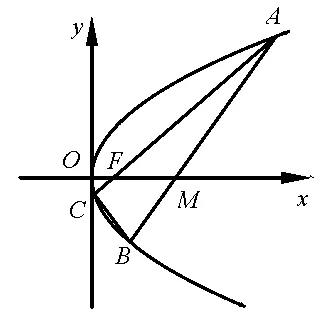
图1
分析本题常规思路是直接去求两个三角形的面积,进一步去寻找坐标之间的关系,运算中发现与坐标相关的式子形式不对称,直接使用韦达定理会有一定的运算量.这里我们通过引入中间变量(即ΔACM 的面积)将面积之比转化为边长之比,进一步转化为坐标之比,然后找寻坐标之间的关系,从而达到消元的目的,简化求解过程.
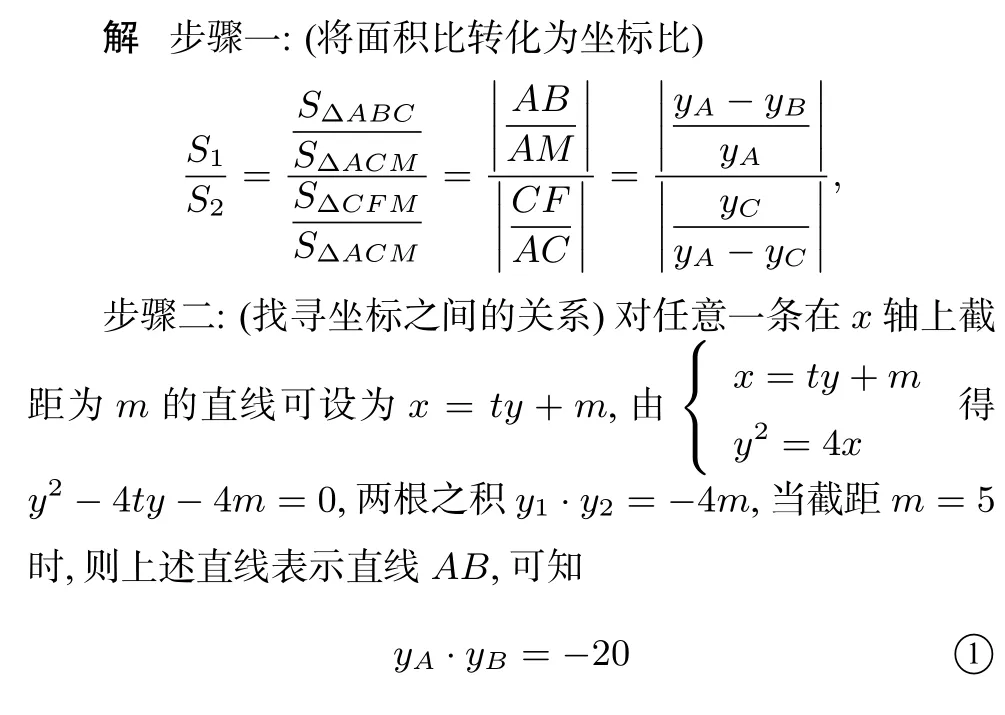
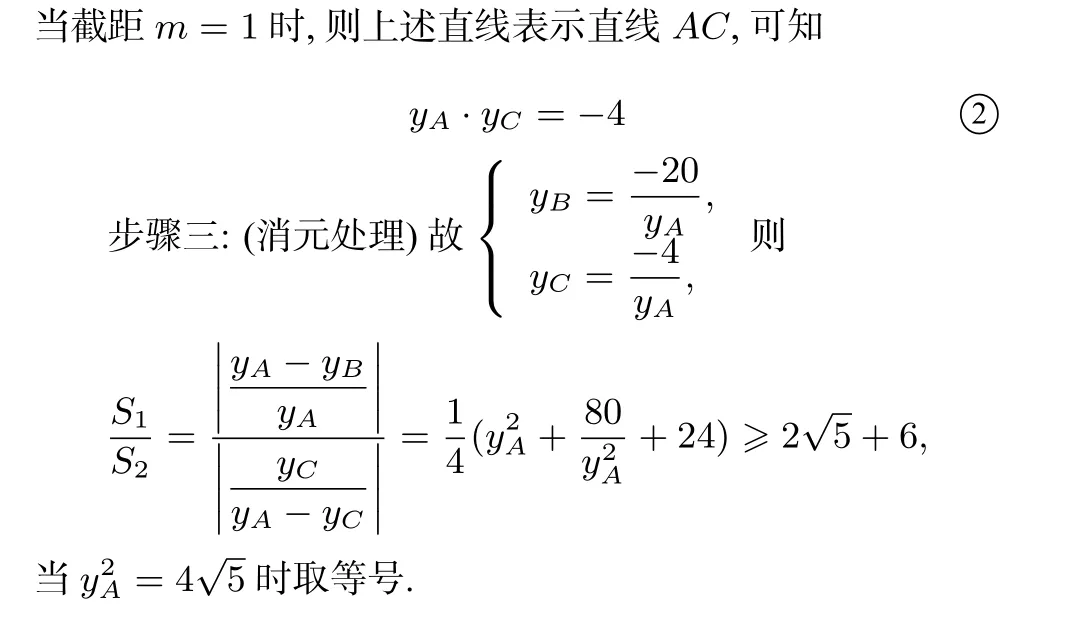
注找准直线的设法,通过韦达定理发现抛物线与直线交点的坐标之积只与直线在坐标轴上的截距有关.抓住这一点,有助于快速找到坐标之间的联系,达到消元的目的.
2 模型应用
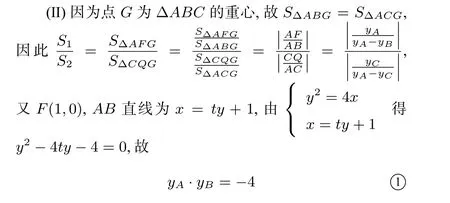
例2(2019年高考浙江卷)如图2,已知点F (1,0)为抛物线y2=2px 的焦点,过点F 的直线交抛物线于A,B 两点,点C 在抛物线上,使得ΔABC 的重心G 在x 轴上,直线AC 交x轴于点Q,且Q 在点F 的右侧,记ΔAFG,ΔCQG 的面积分别为S1,S2.
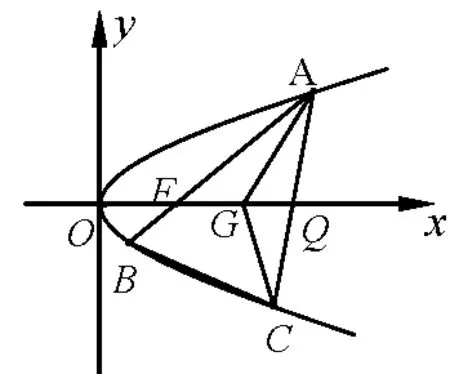
图3
(I)求p 的值及抛物线的标准方程;
分析若按照常规的解法,在转化过程中利用韦达定理得到的两根关系不能整体带入,因此对化简造成了较大困难.这里我们通过引入中间变量(即ΔABG 与ΔACG 的面积)把面积之比转化为边长之比,进一步转化为坐标之比,然后找寻坐标之间的关系,从而达到消元的目的,简化求解过程.
解(I)由题意,p=2,抛物线方程为y2=4x,

评注与例1 相仿,解决直线与抛物线有关的问题时,要注意当直线过轴上定点时,两个交点的坐标之积为定值.同时,本题也要牢牢抓住三角形重心的性质,一方面,重心与三角形各顶点的连线将三角形面积三等分;另一方面,重心坐标与三角形三个顶点的坐标又紧密联系.本题还有许多其他解法,这里不再展开.
例3抛物线y2=2px(p>0)上纵坐标为-p 的点M 到焦点的距离为2.
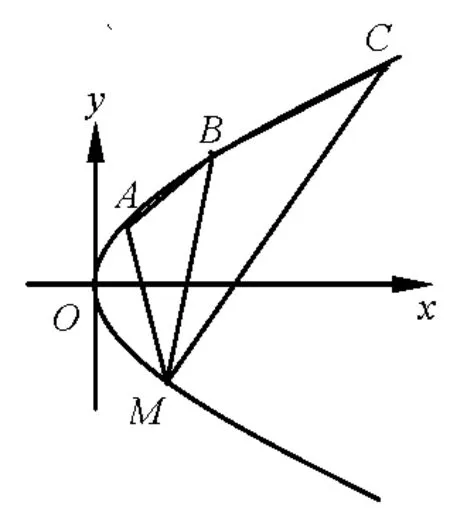
图3
(I)求p 的值;.
(Ⅱ)如图3,A,B,C 为抛物线上三点,且线段MA,MB,MC 与x 轴交点的横坐标依次组成公差为1 的等差数列,若ΔAMB 的面积是ΔBMC 面积的,求直线MB 的方程
解(I)由已知,p=2,M(1,-2),y2=4x;


评注本题也可以利用点A 到直线MB 的距离公式,直接将ΔAMB 面积表示出来,同理表示ΔBMC 得面积,从而进行求解.而上述解法通过将面积比转化坐标比,可适当简化计算求解过程.
例4如图4,已知点A(4,4)在抛物线y2=2px 上,过点B(1,1)的直线交抛物线于点P(x1,y1),Q(x2,y2),其中2 <y1<4.
(I)求y2的取值范围;
(Ⅱ)若直线AP 与OQ 交于点I,记ΔIPQ,ΔIAO 的面积分别为S1,S2,求的最小值及此时点I 的坐标.
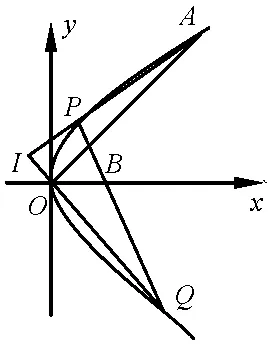
图4

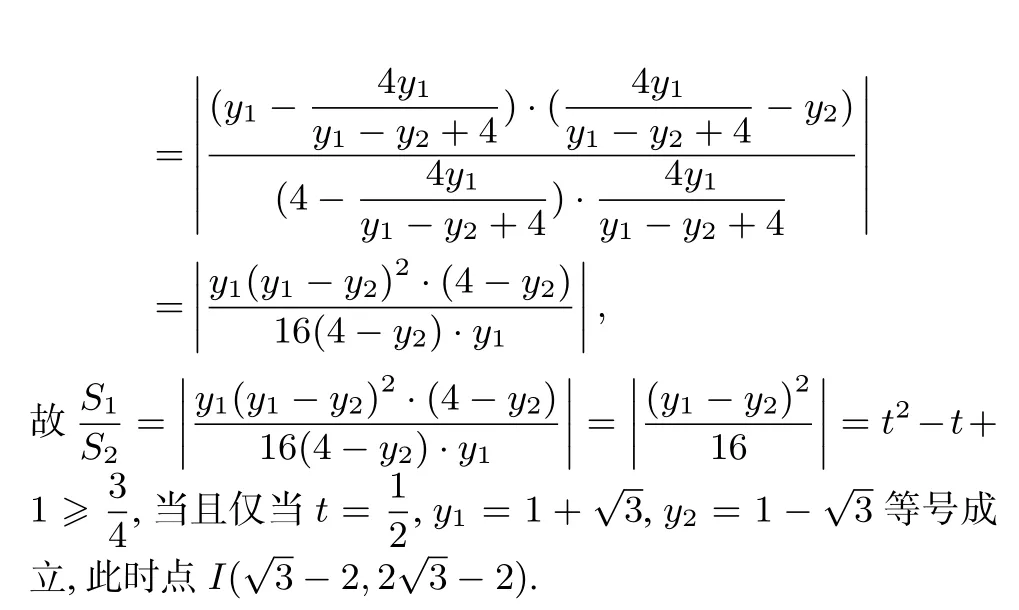
注记解决本题的关键也是将三角形面积比转化为坐标比,尽管用坐标表示的式子形式不对称,但最终发现不对称的因式可以被约去,这也是我们在解析几何求值化简过程当中常常遇到的情况.
3 方法总结
涉及到抛物线中的三角形面积之比问题,往往可以通过以下几个步骤进行操作:
1.寻找同底或等高的三角形(中间变量),将三角形面积之比转化为边长之比,进一步转化为坐标比.
2.联立抛物线与直线方程,通过韦达定理寻找坐标之间的关系,尤其是当直线过坐标轴上定点时,抛物线与直线交点的坐标乘积为定值.
3.利用坐标之间的等量关系,进行消元处理,化为单变元问题后进行求值或求范围.
总之,合理假设直线方程,表示出坐标之间的关系,将面积之比转化为坐标之比,是解决此类问题的关键,这也是圆锥曲线坐标化的意义所在.

