基于Savitsky法滑行艇航行姿态参数影响研究

朱云翔

(海装上海局驻上海地区第八军事代表室，上海 200011)

滑行艇可用做巡逻艇、垂钓艇、勤务艇、救护艇、娱乐艇及体育竞技艇[1]。随着航速的提高，船舶的航态会因流体动支持力的大小与作用位置不同而发生变化，因而船舶的吃水、水线长度及纵倾角也都随航速的变化而发生明显改变。当容积傅汝德数Fr>3.0时，此时航速很高，船体吃水变化很大，而且整个船体被托起并在水面上“滑行”，仅有一小部分船体表面与水接触。滑行艇滑行时，静浮力很小，艇体几乎完全由流体动升力来支持。

Savitsky[2]根据大量试验结果提出了关于计算底部斜升角不变的棱柱形滑行艇水动升力的半理论半经验公式，即英美等较普遍应用的Savitsky法。Liu和Wang[3]用双体滑行艇进行了一系列试验，通过对Savitsky法中的相关系数进行修正，推导出改进后的Savitsky公式，可用于双体滑行艇的阻力计算。Lai和Troesch[4]基于涡格法提出三维线性数值模型用于解决滑行艇稳定滑行问题。模型计算的结果与Savitsky的结果以及试验结果吻合一致。Zhao等[5]基于势流理论的边界元方法，提出2.5D(2D+t)的方法用于分析静水中高航速的滑行艇。Faltinsen[1]给出了关于滑行艇水动力相关的详细分析。Ghassemi和Ghiasi[6]给出了一种组合方法用于预报滑行艇的水动力性能：基于势流理论的边界元法求解兴波阻力，基于边界层理论求解摩擦阻力，基于经验公式求解喷溅阻力。通过四种不同船型的验证分析，Ghassemi组合方法的预报结果与试验结果吻合较好，可用于评估平板和各种具有恒定和可变斜升角的棱柱滑行艇的水动力性能。随着计算流体力学(CFD)不断发展，基于求解RANS方程的CFD方法可以计入滑行艇高速滑行时非线性与黏性影响，具有较高的准确性。Jiang等[7]利用商业软件STAR-CCM+对三体滑行艇进行了数值模拟，通过与试验数据的比较，验证了计算结果的正确性，同时分析了直截面长度参数对三体滑行艇的水动力和气动性能的影响。

Savitsky法计算简单快捷；RANS方法计算耗时，比Savitsky法准确，可以得到更多的流场特性[8]。Savitsky法可用于滑行艇的初步设计，在参数影响与优化研究方面有一定的优势。

采用半经验半理论的Savitsky法对棱柱形滑行艇的航行姿态与阻力进行研究分析，纵倾结果与Fridsma[9]试验结果吻较好，验证了程序的可靠性。然后改变长宽比、重心纵向位置与底部斜升角参数，进一步研究三种参数对滑行艇航行姿态与阻力性能的影响与敏感度分析。

1 滑行艇航行姿态计算方法

1.1 半经验半理论的Savitsky法

Savitsky 1964年根据大量试验结果数据提出了关于计算底部斜升角不变的棱柱形滑行艇水动升力的半理论半经验公式，给出升力系数可表示为

(1)

式中：第一项为无因次静浮力项，第二项为无因次动浮力项。

平均浸湿长宽比λw，λw=0.5(LK+LC)/B，LK和LC分别是龙骨线和折角线的浸湿长度。Savitsky公式中假设的船体是棱柱形的，此时滑行艇的底部斜升角是常数。

(2)

1.2 静水中航行姿态计算与步骤

图1 棱柱形滑行艇受力分析

航行姿态指滑行艇在高速航行过程中的纵倾与升沉变化。如图1所示，设滑行艇在静水以恒定速度航行时，达到稳态，且所有受力均通过船体重心COG，通过关于棱柱形滑行艇的经验公式，满足所有垂向力和纵摇力矩的平衡条件，可计算滑行艇在静水面中滑行时的浸湿长度，航行纵倾，航行阻力等。图中：T表示推力，Rv表示阻力，Mg表示重力，N表示压力。以重心位置为坐标原点，平行龙骨向船首方向为x轴正方向，垂直于龙骨向上为z轴正方向，建立坐标系。

Savitsky法主要计算步骤如下：

1) 平均浸湿长宽比λw

假设所有力都穿过重心，则重心纵向位置lcg与沿龙骨方向从方尾到水动压力中心处的距离lp相等。根据压力中心的纵向位置与平均浸湿长宽比的关系，可求得静水滑行时的平均浸湿长宽比λw。

(3)

式中：lp是沿龙骨方向从方尾到水动压力中心处的距离。

2) 纵倾角τdeg

高速滑行状态下，船体受到的浮力很小，升力成为主要支撑力，忽略了浮力的影响，升力和重力平衡。即FLβ=Mg则有：

(4)

根据Savitsky经验公式：

(5)

(6)

通过迭代法求取非线性方程的根，得到滑行的纵倾角度τdeg。

3) 浸湿长度

定义长度xs=LK-LC，它是沿龙骨方向，从龙骨线和静水面(平均自由面)的交点到折角线浸湿起点的距离。其中LK为龙骨浸湿长度，LC为折角线浸湿长度。

对于折角处没有发生流动分离的横剖面，可以通过使用相似解或者Wagner关于楔形体以常速入水的解来估算垂向力，进而估算流动分离发生的位置。从Wagner解开始，意味着折角线的流动分离从x=xs=LK-LC开始，这里xs满足：

(7)

(8)

根据Dobrovol’ skaya关于刚性楔以常速入水的相似解，给出了一楔形体以恒定的垂向速度V入水过程的砰击参数，其中zmax为最大压力处的z坐标值。

表1 相似解给出的入水过程的砰击参数

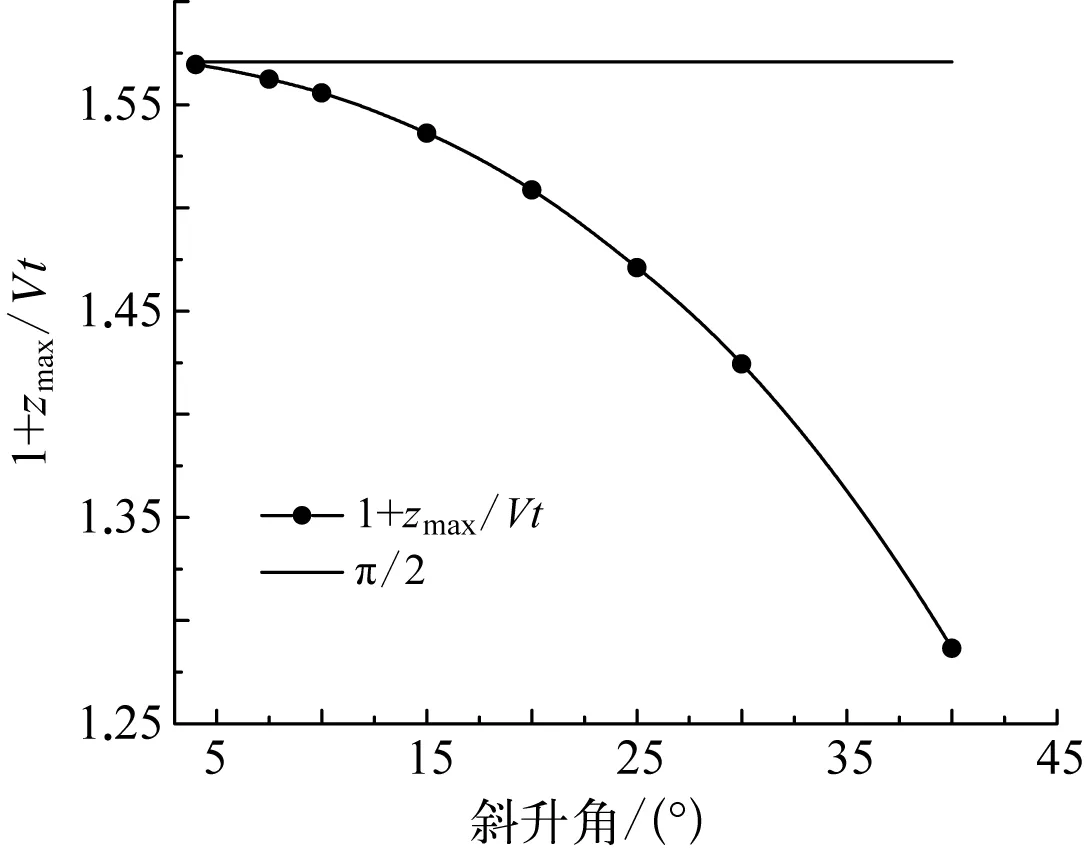
图2 xs的系数随斜升角变化的关系

折角线浸湿长度LC和龙骨浸湿长度LK可以表示为：

(9)

则有：

LC=λwB-0.5xs

(10)

LK=2λwB-LC

(11)

船尾挡板处龙骨的吃水：

D=LKsinτ

(12)

4) 总阻力的计算

滑行艇的总阻力分为两部分：一部分是由于黏性引起的摩擦阻力；另一部分是升力诱导的阻力部分。

诱导阻力通过下式进行计算，即压力造成的阻力分量RP：

FLβ=0.5ρU2B2·CLβ

(13)

RP=FLβτ

(14)

摩擦阻力部分：浸湿面积可分为两部分，从船首部(x=0)一直到折角线浸湿起点处(x=xs)的浸湿面积S1，被用来表示喷溅根部以下的艇体湿表面积。实际上，这部分湿表面积可能更大些。导入d(x)作为从喷溅根部到龙骨线的垂向距离，有：

(15)

将从龙骨线和静水面的交点到折角线浸湿起点的距离xs代换后，有：

(16)

从x=xs到船尾挡板的湿表面积：

(17)

总的湿表面积：

S=S1+S2

(18)

计算总阻力：

Rt=RP+0.5(Cf+ΔCf)ρU2S

(19)

(20)

2 棱柱形与常规型滑行艇数值结果与分析

2.1 棱柱形滑行艇数值结果与分析

为了对该计算程序进行验证，选用Fridsma[9]发表的等斜升角系列模型进行计算，滑行艇基本参数如表2所示，并和试验结果进行比较。表中，L/B为长宽比，LCG(%L)表示重心纵向位置占船长的百分比。

图3给出了棱柱形滑行艇纵倾角的计算结果与试验值的比较。从图3中可以看出：基于Savitsky法计算的纵倾结果与模型试验的结果吻合较好，验证了程序计算的正确性。

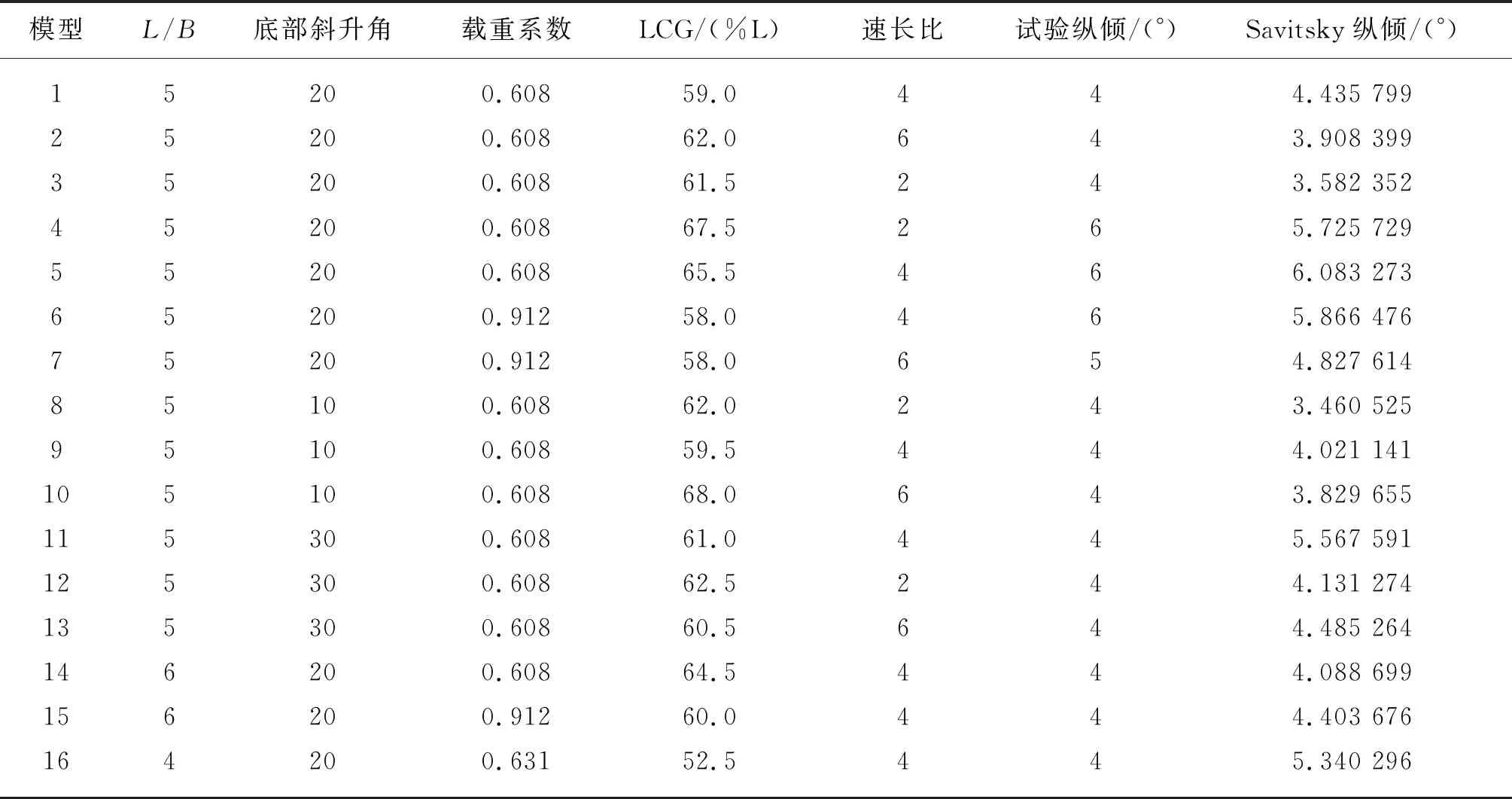
表2 滑行艇基本参数与计算结果比较

图3 棱柱形滑行艇计算结果比较

图4给出了棱柱形滑行艇在不同速长比下的纵倾结果。从图中可以看出：在整个航速范围内纵倾角度的计算结果与试验结果吻合都很好，证明基于半经验半理论的Savitsky方法对于棱柱形滑行艇的姿态计算具有很高的可靠性，可以用以初步设计阶段的选型。

图5给出了不同速长比下滑行艇的阻升比的比较，即给出了计及与未计及喷溅引起湿表面积的增加的阻升比的结果。式(18)在计算湿表面积时计及了喷溅引起的湿表面积的增加，采用式(21)计算时，未考虑喷溅引起的湿表面积的增加。

(21)

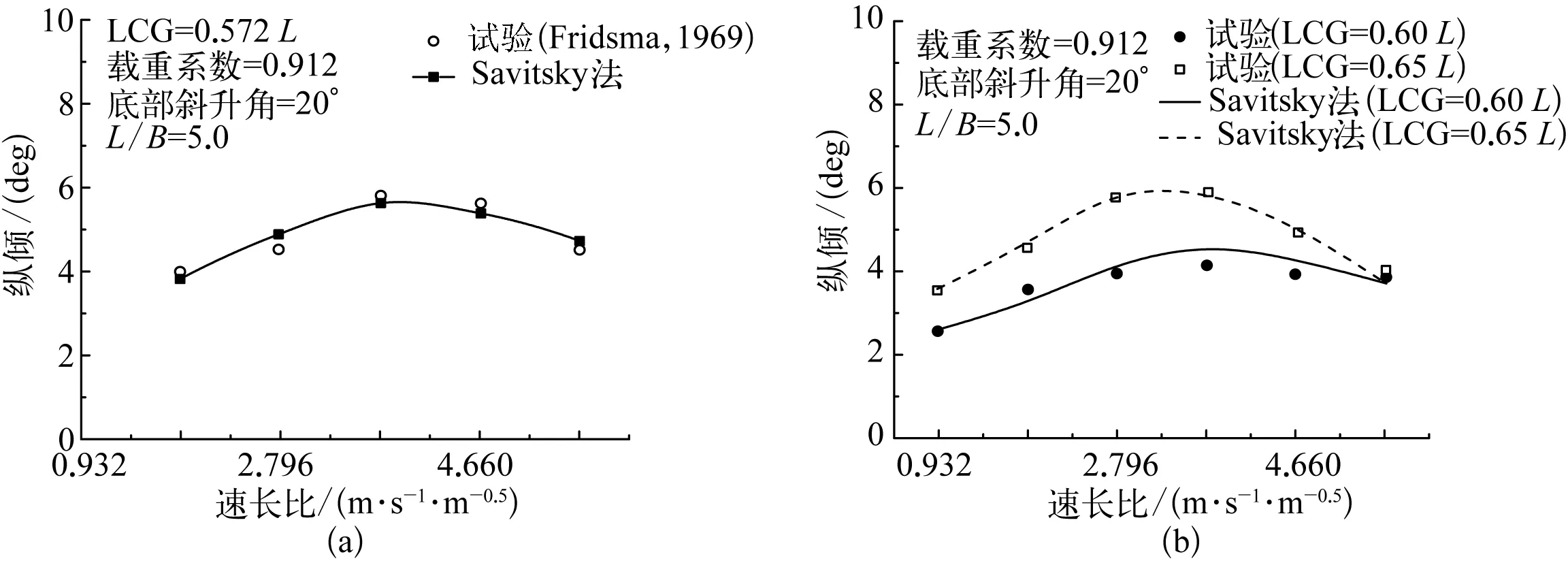
图4 在不同航速下棱柱形滑行艇纵倾结果的比较

从图5中可以看出：随着航速的增加，滑行艇的阻升比逐渐增加；在低速时两种情况下的阻升比基本一致，说明低速时喷溅对于阻力的影响很小；高速时两种情况下的计算结果出现偏差，并且随着航速的进一步的增加，两者的差距越来越大，说明喷溅在高速时比较严重，对于阻力的影响较大，应考虑其影响。

图5 计及与未计及喷溅引起湿表面积的增加的阻升比结果比较

图6 滑行艇横剖面示意

2.2 常规型滑行艇数值模拟与结果分析

选取大阪府立大学Katayama 2000年开展的滑行艇模型试验进行验证计算[10]。滑行艇的主尺度如表3所示，表中，KG表示重心距基线的距离，LCG表示重心纵向位置。滑行艇的横剖面图如图6所示。

表3 滑行艇主尺度

滑行艇高速滑行时，随着航速的变化，滑行艇的姿态包括升沉与纵倾会发生变化。如图7与8所示，同时采用CFD方法模拟计算了滑行艇的航行姿态，给出了不同计算方法对于滑行艇姿态的计算结果与试验结果的比较。可以看出：整个航速范围内，基于CFD模拟计算的姿态变化与试验值吻合较好；在未滑行阶段Fr<0.8范围内数值计算结果与试验值误差较大，在滑行以后，两者差别不大。基于CFD的数值模拟结果在整个速度范围内与试验值吻合较好，尤其是升沉变化曲线与试验结果基本一致。采用Savitsky方法的计算结果与试验结果有一定的差别，整体的变化趋势与试验结果保持一致。

图7 滑行艇纵倾变化

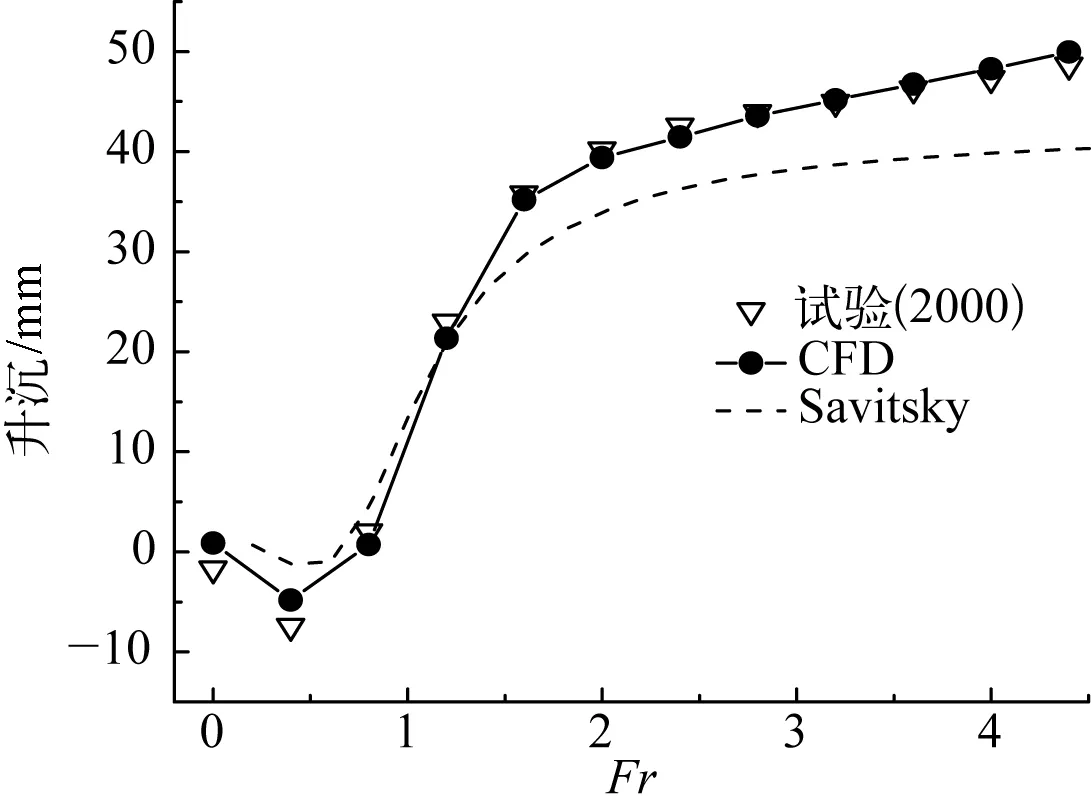
图8 滑行艇升沉变化

3 滑行艇阻力性能参数影响研究分析

由于CFD数值计算耗时较长，采用Savitsky法对滑行艇进行参数影响研究。在Fridsma[9]系列模型试验的基础上，基于Savitsky法通过改变滑行艇的长宽比、底部斜升角与重心纵向位置参数来研究其对阻力性能的影响。选取的基准模型主尺度如表4所示。

表4 模型主尺度

3.1 长宽比影响

从流体动力性能方面考虑，滑行艇的宽度越大，相当于增加了滑行面的展弦比，有利于提高滑行效率，但同时会增加浸湿面积，导致摩擦阻力的增加。图9给出了长宽比分别为4.5、5.0与5.5三组模型在不同航速下的结果比较。

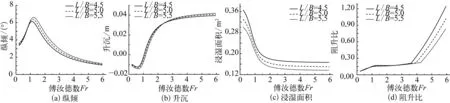
图9 三种长宽比的结果比较

从图9(a)可以看出：整体上，随着航速的增加，纵倾角先增加，后减小，最后趋于稳定。在傅汝德数为1.2 左右，纵倾角有一峰值；长宽比越大，峰值越大，峰值的位置向右偏移。在傅汝德数大于1.2范围内，同一航速下，长宽比越大，纵倾角越大。从图9(b)看出：在相同航速下，三种长宽比的升沉差别较小，说明升沉对长宽比的变化不敏感，影响较小。从图9(c)看出：整体上，随着航速的增大，浸湿面积逐渐减小；航速进一步增大，浸湿面积趋于定值。相同航速下，长宽比越大，浸湿面积越大。从图9(d)看出：低航速时，三种长宽比下的阻升比接近；在傅汝德数大于3.5的范围内，长宽比越大，阻升比也越大，由于航速较高，喷溅引起浸湿面积对阻升比影响较大。

3.2 重心纵向位置影响

滑行艇重心纵向位置的不同会直接影响姿态的变化，进而影响其静水阻力性能。这里的重心纵向位置用重心到方尾的纵向距离占滑行艇总长的比重来表示。重心纵向位置LCG/L分别选取0.35、0.40、0.45展开研究，图10给出了不同重心纵向位置时，不同航速下滑行艇的静水阻力性能与姿态。

从图10(a)看出：重心纵向位置越靠近船尾，纵倾角的峰值越大，三种不同重心纵向位置的纵倾峰值差别较大，说明重心纵向位置对于纵倾角的影响较大，由于重心纵向位置与纵摇的惯性力矩有关，纵向的惯性半径主要取决于滑行艇的重心纵向位置与底部的形状。从图10(b)看出：三种不同重心纵向位置下，低航速时，重心越靠近船尾，滑行艇下沉值越大；高航速时，升沉结果基本一致。从图10(c)看出：相同航速下，重心越靠近船尾，浸湿面积越小，由纵倾角较大引起的。从图10(d)看出：低航速时，重心越靠后，阻升比越大，可能由于低航速时滑行艇的下沉值较大引起的；高航速时，重心越靠后，阻升比反而越小，与浸湿面积的变化有关。

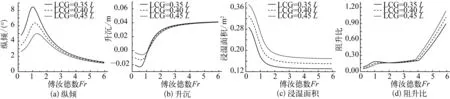
图10 三种重心纵向位置的结果比较

3.3 底部斜升角影响

滑行艇的横剖面往往都采用舭部有折角的斜升型，也称V型。如图11所示，文中选取底部斜升角分别为10°、20°与30°，研究不同斜升角对滑行艇的姿态与阻力性能的影响。图12给出了不同底部斜升角时，不同航速下滑行艇的静水阻力性能与姿态。从图12(a)与(b)看出：在相同航速下，斜升角越大，纵倾角越大，升沉值越小。从图12(c)与(d)看出：浸湿面积随着底部斜升角的增大而增大。在傅汝德数大于3.5范围内，随着底部斜升角的增大，滑行阻力增大，滑行的效率降低。

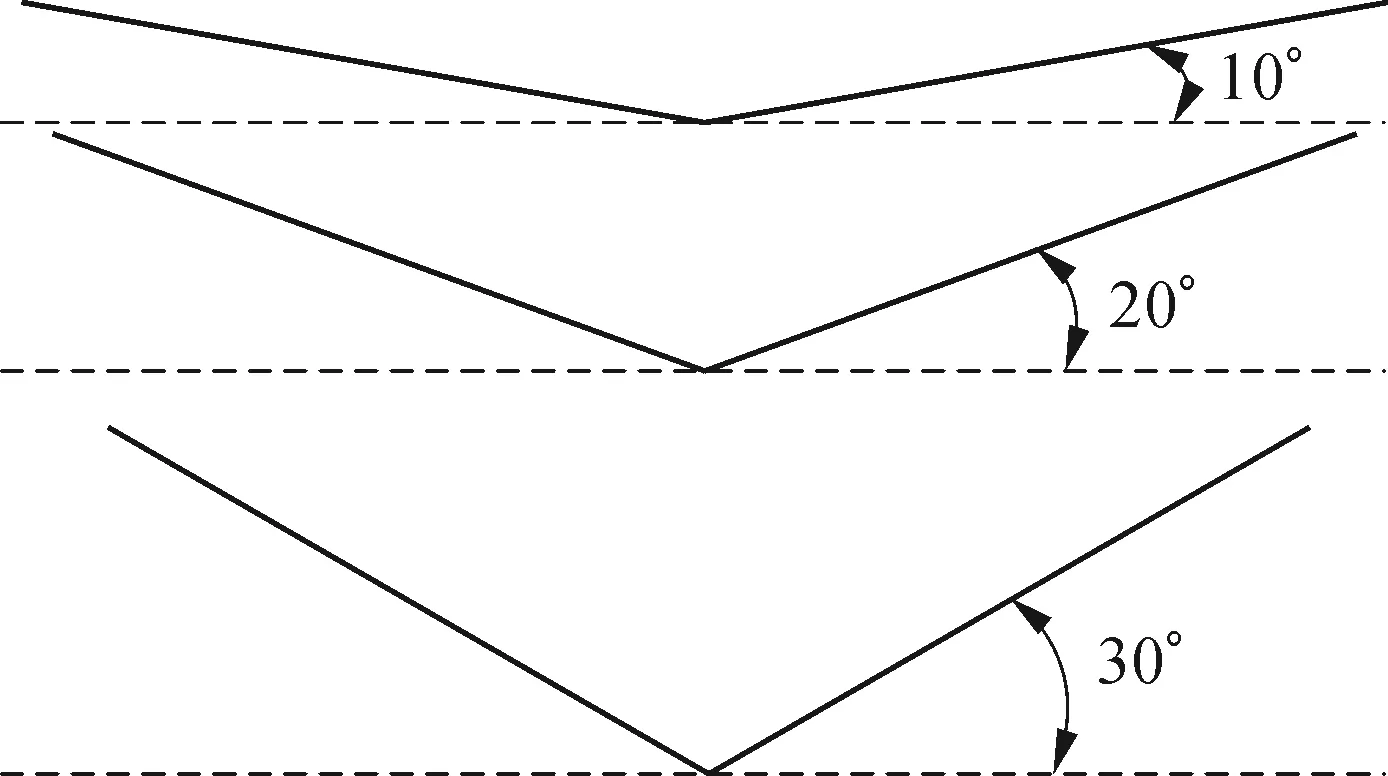
图11 三种底部斜升角示意

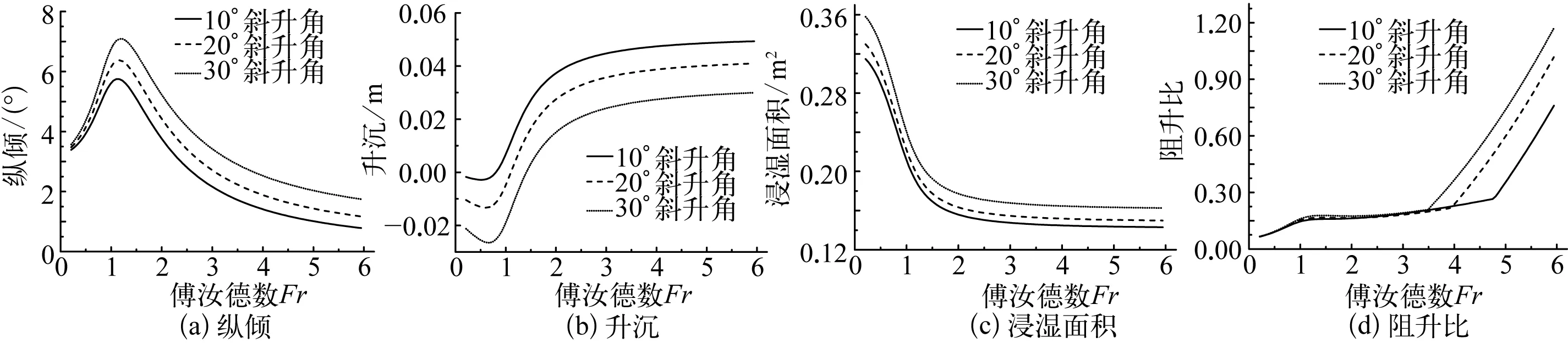
图12 三种底部斜升角的结果比较

4 结 语

采用Savitsky法对滑行艇的阻力与航行姿态进行研究分析。通过与CFD数值结果和试验结果比较，验证分析了半经验半理论Savitsky方法的正确性。进一步研究分析了滑行艇的长宽比、底部斜升角与重心纵向位置参数对棱柱型滑行艇航行姿态与阻升比的影响。主要结论如下：

1) 基于Savitsky法计算棱柱形滑行艇的航行姿态，计算效率高，并具有可靠的适用性。采用Savitsky法计算滑行艇阻力时，在高速阶段应计及喷溅引起湿表面积增加的阻力增加。

2) 随着航速的增加，滑行艇的纵倾角先增加后减小最后趋于稳定；升沉值先减小，后逐渐增大；浸湿面积先减小，后趋于稳定。

3) 滑行艇的纵倾角对长宽比变化不敏感，重心纵向位置与底部斜升角对纵倾角影响较大。同航速下，重心纵向位置越靠近船尾，纵倾角越大；斜升角越大，纵倾角越大。

4) 滑行艇的升沉值对长宽比与重心纵向位置变化不敏感，升沉结果对底部斜升角比较敏感。斜升角越大，升沉值越小。

5) 滑行艇在低速时，长宽比、重心纵向位置与底部斜升角的变化对阻力影响较小；高速时，阻力值对三种参数比较敏感。滑行艇的长宽比越大，重心纵向位置越远离船尾，底部斜升角越大，阻力结果越大。