基于基因表达式编程算法的波浪透射预测
刘 涛,冯 曦,冯卫兵,张宸豪,陆 杨
(1. 海岸灾害及防护教育部重点实验室(河海大学),江苏 南京 210098; 2. 河海大学 港口海岸与近海工程学院,江苏 南京 210098; 3. 南京水利科学研究院,江苏 南京 210029)
波浪透射预测是海洋工程中的一项基础性研究,它对于维护港口水域平稳、船舶稳定以及海岸泥沙输移等有着深远影响。因此,准确预测波浪透射对于海洋工程极其重要。
大型深水防波堤堤后波浪一般来自两个方面,其一是堤顶越浪,其二则是堤身渗透波浪。针对越浪的情况,国内外学者已经做了大量的研究[1-4],得到的成果可以很好地应用到实际工程中。但是对于不可越浪的防波堤透浪研究,国内外的成果相对较少。
波浪透射的程度,通常用透浪系数来表述,其定义如下:
Kt=Ht/H
(1)
式中:Kt为透浪系数,Ht为堤后波高,H为入射波高。透浪系数的大小反映了波浪在堤内的衰减程度,Kt越小,衰减越显著。目前研究波浪透射主要从理论推导和物理模型试验两种方法入手。理论研究方面,Sollitt和Cross[5]假设抛石斜坡堤的断面是矩形结构,忽略了黏性项和对流项的影响,利用数学推导得到波浪透射系数的解析解,此后国内外学者开始关注波浪与多孔介质相互作用的问题。Madsen[6]利用线性波理论得到波浪在堤内的衰减公式。Stephenson[7]假定水头损失处在阻力平方区,推导出半理论半经验计算公式,得到的结果通过试验数据验证较为满意。
物理模型试验方面,王登婷和左其华[8]、葛晓丹[9]和Sokolewicz[10]等做了大量的物模试验,阐明了影响波浪透射的因素主要分为两方面:一方面是波浪本身的特性,比如波高、波周期和波陡等;另一方面由防波堤的结构决定,堤宽、中值粒径和堤前水深等均有较大影响。
以上学者的研究都带有一定的局限性,理论推导需要简化模型,而物模试验又受限于比尺效应,致使提出的公式只能应用在一个限定的范围内。近年来,随着人工智能技术,如遗传算法、人工神经网络和基因表达式编程(gene expression programming, 简称GEP)算法等被引进海洋工程,极大地促进了这些学科的发展。Deo和Jagdale[11],Jain和Deo[12]利用人工神经网络来模拟波浪的传播;Robertson等[13]将GEP算法运用到波浪破碎问题中,解决了近海波浪破碎条件难以精准预测的问题;Ebtehaj和Bonakdari[14]采用GEP算法模拟泥沙运输;Power等[15]利用GEP算法来预测波浪爬高,均取得了不错的进展。
针对传统研究方法较难准确预测波浪透射的问题,采用GEP算法预测规则波作用下不越浪防波堤的波浪透射系数,研究GEP算法预测精度随训练组数变化的规律,比较GEP算法与各家经验公式的优劣,并通过对各影响变量进行敏感性分析,确定影响波浪透射的最显著因素。
1 试验数据
数据是GEP算法运行的基础,精准评估各家透浪系数计算公式也要更多详细数据的支撑。开展的物理模型试验在水槽中进行,水槽尺寸为90 m×0.5 m×1.0 m(长×宽×高)。试验采用规则波,试验布置如图1所示。入射波是由水槽前端推板式造波机生成,水槽末端设置斜坡式消浪板进行消浪,有效减小波浪反射的影响。波高是通过布置在防波堤前后的四根浪高仪来采集,浪高仪采用DJ800,采集频率为50 Hz。防波堤坡度为1∶1.5,护面型式采用单层扭王字块,单个扭王重370 g,堤心石采用有棱碎石,粒径变化范围为0.008~0.032 m。
此外,为了提高GEP算法的预测能力和评估各家公式的精准度,本次研究还收集了前人的试验数据,形成一个庞大的透浪试验数据库,共计567组,代表了各种波浪条件(0.002 m≤H≤0.24 m,0.71 s≤T≤7 s)。试验水深的变化范围是0.2 m≤d≤0.5 m,涵盖实验室水槽大部分水深情况。静水面堤宽是影响波浪透射的重要因素,堤宽最小只有0.08 m,最宽达到1.7 m。堤身中值粒径的变化范围0.013 m≤D50≤0.055 m。表1为文中用到的试验数据。
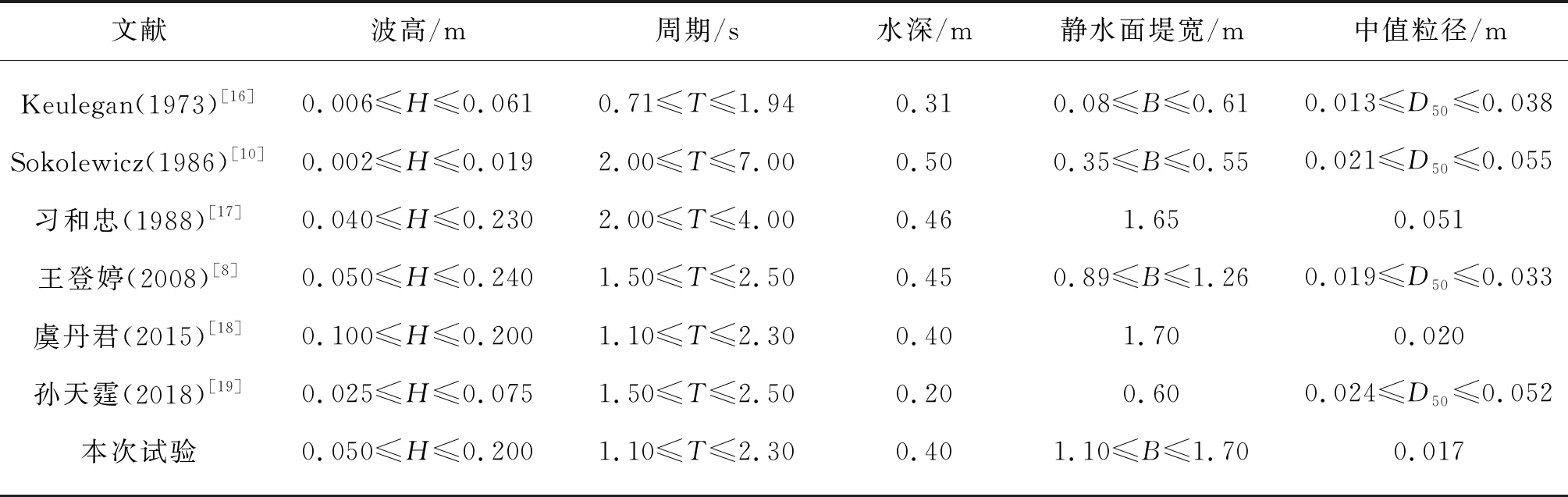
表1 试验数据
2 研究方法与内容
2.1 算法介绍

图2 GEP染色体和表达式树
基因表达式编程(GEP)算法是由Ferreira于2001年在遗传算法和遗传编程的基础上提出来的,它既有遗传算法“定长线性串”的简单特性,也有遗传编程“动态树结构”的搜索能力[20],是一种基于生物基因结构和功能发明的新型自适应演化算法。GEP算法通过模拟生物遗传进化采用概率化的寻优方法,自适应调整搜索方向,极大地加快了收敛速度。如图2所示,GEP算法借鉴了生物学的开放读码框架(ORF)概念,并且采用表达式树(ET)来进行解码,相较于其他遗传算法,简化了算法编码,提升了计算效率。
GEP算法的进化流程:首先随机给出一个初始化种群,然后通过ET来表达染色体,接着确定这个种群是否满足预设的终止条件,终止条件一般选择最大进化代数或计算精度。如果满足,保留最优个体输出。如果不满足,则需要对这个种群采用一系列的遗传操作算法,如变异、倒串、基因重组等等,形成一个新的种群,再接着上一轮的操作,直到满足终止条件为止。
2.2 波浪透射预测的GEP算法
2.2.1 输入变量
根据前人研究成果[6-10],入射波高(H)、波周期(T)、水深(d)、静水面堤宽(B)和堤心石中值粒径(D50)对于波浪透射影响较大。结合影响波浪透射的两个方面:波浪特性和防波堤结构,对各影响变量进行无量纲化,考虑深水波陡(H/gT2)、相对波高(H/d)、相对堤宽(B/D50)和相对水深(d/L)对波浪透射的影响,设置了6组变量组合。比较不同组合情况下GEP算法对波浪透射的预测能力,确定最优组合,建立透浪系数表达式。表2是本次研究的GEP算法参数设置。
采用以下几个统计参数作为评价指标:均方根误差(RMSE)、标准均方差(NMSE)、决定系数(R2)和平均预测误差(BIAS)。它们的计算如下:
(2)
(3)
(4)
(5)
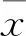
RMSE和NMSE越小代表预测值越精确,R2越接近1表示预测效果越好,当BIAS为正数时表示预测值大于试验值,BIAS为负数时表示预测值小于试验值。

表2 GEP算法参数设置
2.2.2 输入样本数量
为了探究GEP算法的预测精度与输入样本数量之间的关系,将数据分成训练组和验证组,训练组中的数据以50组为间隔逐渐增加,验证组的数据用于比较不同组次对波浪透射的预测效果。定量评估不同组次的预测精度,除了式(2)~(5)几个指标外,定义了“精度区间”,即预测理想值±2倍均方根误差。为了方便统计,此处的均方根误差采用统一值,即不同组次中均方根误差的平均值。
2.3 透浪系数经验公式
本次研究选取了两家不越浪防波堤透浪系数计算公式,用于对比分析GEP算法的预测能力。
2.3.1 Madsen公式
Madsen[6]假定水头损失与速度为线性,堤内是完全紊流状态,利用线性波理论推导出波浪在堤内衰减状况,公式如下:
(6)
式中:Kt为透浪系数,H为入射波高,B为堤身宽度,d为水深,β为恩格隆摩擦系数,
(7)
式中:n为孔隙率,D50为名义中值粒径。
2.3.2 Stephenson公式
Stephenson[7]认为水流处在阻力平方区,水头损失与速度平方成正比,通过理论推导并简化,得到防波堤透浪系数计算公式:
(8)
式中:μ为阻力系数,一般是雷诺数和石头形状系数。Stephenson根据试验结果归纳出μ的计算式:
(9)
式中:Re为雷诺数,μt为形状系数,光滑球状块石μt=1,半圆砾石μt=2,有棱碎石μt=3。
3 结果分析与讨论
3.1 最优输入变量组合
随机地选择80%的数据(454组)用于训练,剩余20%的数据(113组)用于验证,考虑深水波陡(H/gT2)、相对波高(H/d)、相对堤宽(B/D50)和相对水深(d/L)对波浪透射的影响。表3给出了不同方案的GEP算法对波浪透射预测效果的评价结果。方案4没有考虑相对堤宽的影响,相对于其他方案预测精度较低,表明相对堤宽对于波浪透射影响较为显著。方案6考虑了4个变量的影响,但是预测精度仍不及方案1、2、3和5。方案3中验证组的表现优于其余方案,在未知试验条件下预测精度最高,因此确定方案3作为GEP算法的最优输入组合,建立的透浪系数计算公式:

(10)
3.2 输入样本数量对GEP算法预测精度的影响
选择67组不同试验条件下的透浪数据来验证输入样本数量的变化对GEP算法预测精度的影响,结果如图3所示。可以看出,当训练组数较少时,GEP算法的预测精度不高,大部分数据处在“精度区间”外,且预测的精度随着训练组数的增加而提高。当训练组数达到300组时,仅有少量数据处在“精度区间”外,说明此时GEP算法已具备较高的预测精度。随着训练组数的继续增加,GEP算法的预测精度提升不大,精度逐渐趋于平稳。表4总结了不同训练组数情况下验证组数据的RMSE、R2和落入“精度区间”占比。不难看出,RMSE和R2的变化也呈现上述规律。

图3 不同训练组数的GEP算法对波浪透射的预测效果
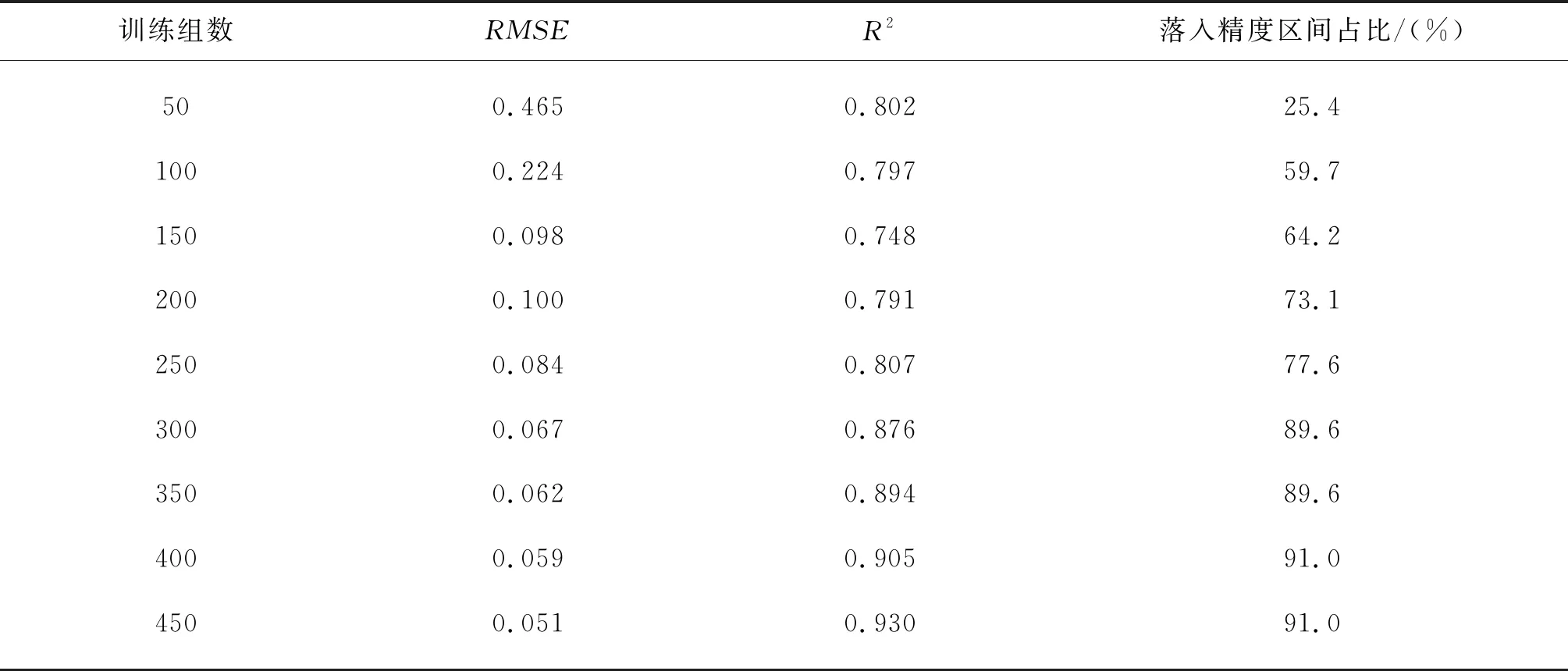
表4 不同训练组数的GEP算法对波浪透射预测效果评价指标
3.3 两家经验公式和GEP算法的预测透浪效果比较
将GEP算法与两家经验公式对波浪透射的预测效果作比较,图4和表5分别从定性和定量上给出了结果。从图4中可以明显看出,无论是训练组还是验证组,GEP算法对于透浪的预测精度大大高于两家经验公式。整体上Madsen公式的表现要优于Stephenson公式,但是Madsen公式在推导过程中没有考虑波浪周期的影响,致使公式在周期较小的情况下预测结果偏差较大。Stephenson公式的预测值一般比试验值大3~4倍,主要原因是公式在推导过程中将液体质点轨迹假设为圆形,但是实际防波堤多建于浅海,液体轨迹已经近似椭圆。由表5可知,GEP算法的所有评价指标相比以上两家经验公式均达到了最小值,其中验证组的RMSE、NMSE和BIAS分别是0.073、0.061和-0.007,R2高达0.858,预测结果较好。

图4 透浪试验值和各家经验公式及GEP算法预测值的比较

表5 各家经验公式与GEP算法对波浪透射预测效果的评价指标
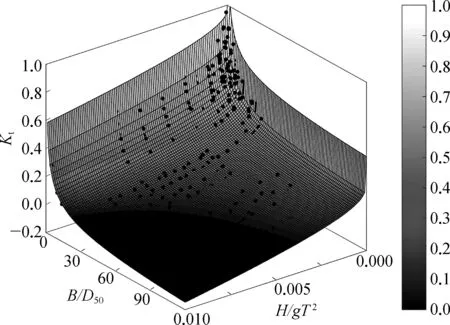
图5 透浪系数随深水波陡和相对堤宽的变化趋势
考虑深水波陡和相对堤宽对波浪透射的影响,绘制透浪系数随二者变化的三维图,如图5所示。图上散点是试验值,曲面是GEP算法预测值。由图可知,GEP算法预测值与试验值吻合良好。当H/gT2和B/D50较小时,Kt随二者的增大而急剧减小,随着H/gT2和B/D50的不断增大,Kt的减小速度逐渐变缓。
3.4 敏感性分析
为了确定各输入变量对波浪透射的影响程度,对每个变量进行敏感性分析。敏感性分析采用偏导数灵敏度分析法[21],利用GEP算法得到的透浪系数显式表达式,对各个变量求偏导,然后计算每一个变量对应的值。当纵坐标为负数,表明透浪系数随变量的增大而减小,二者呈负相关;当纵坐标为正时,则相反,结果如图6所示。从图中可以看出三个输入变量中深水波陡是影响波浪透射的最主要因素。透浪系数与深水波陡、相对堤宽和相对水深均呈负相关,即透浪系数随着三者的增大而逐渐减小。三个输入变量对透浪系数的影响均呈对数分布,表明变量数值越小波浪透射受其影响程度越大。

图6 输入变量敏感性分析
4 结 语
针对规则波作用下不越浪防波堤的波浪透射问题,基于567组透浪试验数据,采用GEP算法预测波浪透射系数,确定了GEP算法的最优输入变量组合并建立了透浪系数显式表达式,研究了GEP算法预测精度的变化规律,主要结论如下:
1) 深水波陡、相对堤宽和相对波高是GEP算法预测波浪透射系数的最优输入变量组合。
2) 当训练数据较少时,GEP算法对波浪透射的预测精度不高,且预测精度随着训练数据的增加而提高。当训练组数达到300组时,GEP算法已具备较高的预测精度,随着训练数据的继续增加,预测精度提升不大。因此,后续的透浪研究工作者可以通过收集前人已做的300组试验数据进行研究,可避免重复性的物理试验。
3) GEP算法对波浪透射的预测精度远远高于前人的经验公式,验证组的RMSE、NMSE和BIAS分别是0.073、0.061和-0.007,R2高达0.858。GEP算法的敏感性分析结果表明,透浪系数随着深水波陡、相对堤宽和相对水深的增加而减小,深水波陡相较于另外两个输入变量影响波浪透射效果更为显著。

