深海采矿系统长距离垂直输运管道力学性能研究

陈智昊，吕海宁，吴 琪

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240； 2. 高新船舶与深海开发装备协同创新中心，上海 200240)

大洋海底中蕴藏着丰富的多金属结核、富钴结壳和多金属硫化物等矿产资源，富含铜、锰、镍、钴、金等多达76种金属元素。据不完全统计，全球海底锰结核含量可达5 000亿吨。然而，这些丰富的矿产资源普遍贮藏在水深一千米以上的深海区域，勘探和开发难度大。在当前全球能源供应紧张的大环境下，深海贮藏的大量矿产资源必将成为未来资源供应的发展趋势和重要渠道。深海矿产资源开发技术的相关研究始于20世纪50年代末，针对多金属结核、富钴结壳和多金属硫化物等矿物的赋存状态和分布特征，美国、日本、韩国、德国和印度等国先后多次开展海上试验并设计研发了多种形式的采矿系统。目前，海底集矿系统和长距离垂直输运系统相结合的开发模式已被证明是深海资源开发工程中最具开发前景的方案[1-3]。

完整的海底矿产资源开发系统，从水面至海底，主要由大型水面支持船、深水悬臂式长距离垂直输运管道、水下大功率提升泵和海底集矿装置等部分组成。其中，长度达上千米的深水悬臂式垂直输运管道是整个系统中最为薄弱，技术难度最大的部分，也是最为关键的核心内容，其流固耦合力学特性的准确预报和分析是深海资源开发的重难点。与传统海洋油气立管相比，深水悬臂式垂直输运管道，其底部处于自由悬垂状态，其力学性能更加复杂和特殊，具有强烈的非线性力学特征和空间运动构型。

在深海剪切流和随机波浪作用下，长距离输运管道的结构强度与安全是悬臂式长距离垂直输运管道安全性问题的核心，其中存在许多问题有待分析和解释，亟待深入探索。肖林京等[4]将输运管简化为管梁模型，根据Morison公式构建了管道在海流、波浪、船舶作用下的运动方程，分析海洋环境条件、中继舱和拖航速度对于管道偏移幅值的影响；郭小刚等[5]建立了大位移弹性杆件与流体相互作用的运动方程，考虑高阶位移量和横向剪力作用并用于预报管线的空间构型；Hatta等[6]考虑了水面船和波浪的激励作用预报了典型节点处的位移、约束力和应力；周知进等[7]采用CFD方法分析了海流作用下管道应力的分布特征和连接点处的应力极限，并对管道分段之间不同的连接方式进行了对比；Hong和Koterayama[8]对比了柔性管道的数值计算和物理模型试验，指出物理模型试验对于理解管道复杂动力响应很有必要；Rahmati等[9]指出，需要设计合理的模型试验,考虑管内外的压力，管体刚度，预张力以及可能出现的大位移和大变形；胡琼[10]建立了长距离输运管道在不同激励条件下的物理试验系统，研究了管道运动、升沉补偿装置以及布放回收过程中系统的水动力性能，分析系统各部件边界条件的影响以及水动力系数等。

下文将深海采矿系统中的长距离垂直输运管道作为主要研究对象，采用势流理论和集中质量法对于管道系统进行计算和分析，并与模型试验的结果进行对照，对于结构的力学性能展开研究和探索。

1 计算原理

1.1 三维势流理论

三维势流理论可应用于计算零航速大尺度结构物的一阶波浪载荷。三维势流理论假定计算流体为无黏、无旋、有势的理想流体，则对于结构物所处流场存在速度势函数，流场的基本控制方程由连续性方程和N-S方程简化为Laplace方程和Lagrange积分。除了满足Laplace方程外，流场还需要满足自由表面条件、物面条件、底部条件、辐射条件等边界条件以及初值条件。

根据势流理论基本假定，一阶速度势Φ(x,y,z,t)的控制方程和定解条件。

拉普拉斯方程流场内：

(1)

自由面条件：

(2)

物面条件：

(3)

底部条件：

(4)

式中：t为时间；g为重力加速度；n为船体平均湿表面上指向内部的单位法向量；Un为船体法向速度。

根据叠加原理，总的速度势可以分解为入射势、绕射势和辐射势：

Φ(x,y,z,t)=ΦI(x,y,z,t)+ΦD(x,y,z,t)+ΦR(x,y,z,t)

(5)

式中：ΦI为入射速度势；ΦD为绕射速度势；ΦR为辐射速度势；ΦD+ΦR=ΦP，合称为扰动势。其中涉及绕射势的绕射问题忽略结构物的运动，只计算波浪对结构物的作用；辐射问题计算由船体运动产生的附加质量和阻尼系数。

1.2 时域耦合分析

对于浮式海洋结构物，耦合时域分析是指考虑结构物主体以及水下管线系统的相互影响后，求解系统运动方程、动力方程的过程。传统解决耦合问题的做法是采用分开求解的办法，即先求解结构物主体水动力，把水下管线系统对它的作用简化成线性回复力；然后将求得的主体水动力视为对水下管线系统的外力，对水下管线系统进行动力分析。这本身是非耦合的方法，忽略了主体部分与水下管线系统相互作用，因而结果不够准确。随着海洋工程技术的迅速发展，水下管线系统的重要性越来越突出，对其耦合问题的研究也越来越深入与完善。对主船体与水下管线系统的耦合问题，现已基本形成一套整体考虑主体和水下管线系统的耦合分析方法，将水下管线系统和结构物主体整体作为分析对象，在每一个时间步中用迭代方法同时求解。耦合求解考虑船体以及水下管线系统的相互影响。

海洋浮式结构物耦合运动的方程：

(6)

该非线性微分方程表示了惯性力、阻尼力、内部结构力、外力与结构位移和速度之间的耦合作用。

惯性力可以表示为：

(7)

其中，M表示系统质量矩阵，包括结构质量矩阵MS、内部流质量矩阵MF及结构加速度的水动力矩阵MH。

阻尼力可表示为：

(8)

其中，C表示系统阻尼矩阵，包括内部结构阻尼矩阵CS(r)、特定离散阻尼矩阵CD(r)以及考虑结构物绕射作用的水动力阻尼矩阵CH(r)。在水动力分析中，还必须包含内部结构的阻尼，因为结构自身有能量耗散。内部结构力RS的计算是基于单元的每一瞬时的应力状态，而外力RE包括重力、浮力、海洋环境载荷、水下管线系统作用力及海底作用力等。

1.3 集中质量法

长距离垂直输运管道的动力响应采用集中质量法计算。集中质量法通过将管道系统分成多个单元，使其简化为具有有限多个质量点，相邻质量点间由无质量的线性弹簧相连的有限元模型，从而将整个系统简化为有限自由度的系统。

集中质量法将管线的单元所受载荷等效成为节点载荷，对每个节点建立运动方程：

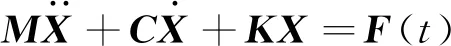
(9)

代入边界条件后即可求解管线各质点的位移X，从而估算管线的动力响应。

管道在波浪和海流中受到的流体作用力根据Morison公式求得：

(10)

其中,CM为惯性力系数，Δ为管线排水量，af为流体加速度(对地)，CD是管线阻力系数，A是管线阻力面积，vf是流体速度(对地)。

2 研究对象

图1为深海采矿系统的总体结构与在软件中建立的模型。结构的相关计算在Orcaflex软件中进行。本次计算水深为1 200 m，海底为水平面，长距离垂直输送管道管长1 170 m，中继站位于水下1 150 m水深处，海底采矿车位于水深1 200 m的海底平面。输送软管连接中继站和海底采矿车，输送软管总长300 m,采用单峰构型。参数的选取符合深海采矿系统的特征，模型具有代表性和典型性。计算总时长为3 600 s，单位时间步长0.1 s。

2.1 水面支持船

将一型甲板驳船作为本研究的水面支持船。水面支持船在采矿系统中与输运管道直接相连，作为管道上方固定端的边界条件，水面船的运动对于管道系统的载荷有着很大的影响。水面船的计算参数见表1。

图1 深海采矿系统总体结构与计算模型

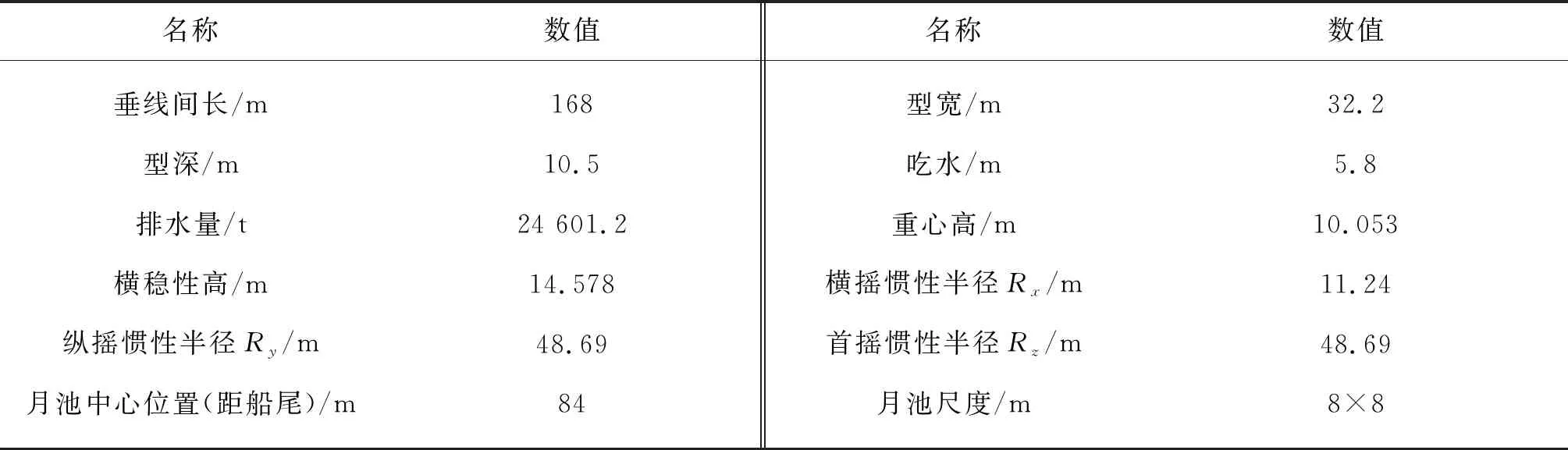
表1 水面船计算参数

2.2 长距离垂直输运管道

长距离垂直输运管道计算总长1 170 m，上端与水面船固定连接，下端连接中继站，处于自由悬垂状态。管道计算模型参数见表2。

表2 长距离垂直输运管道计算参数

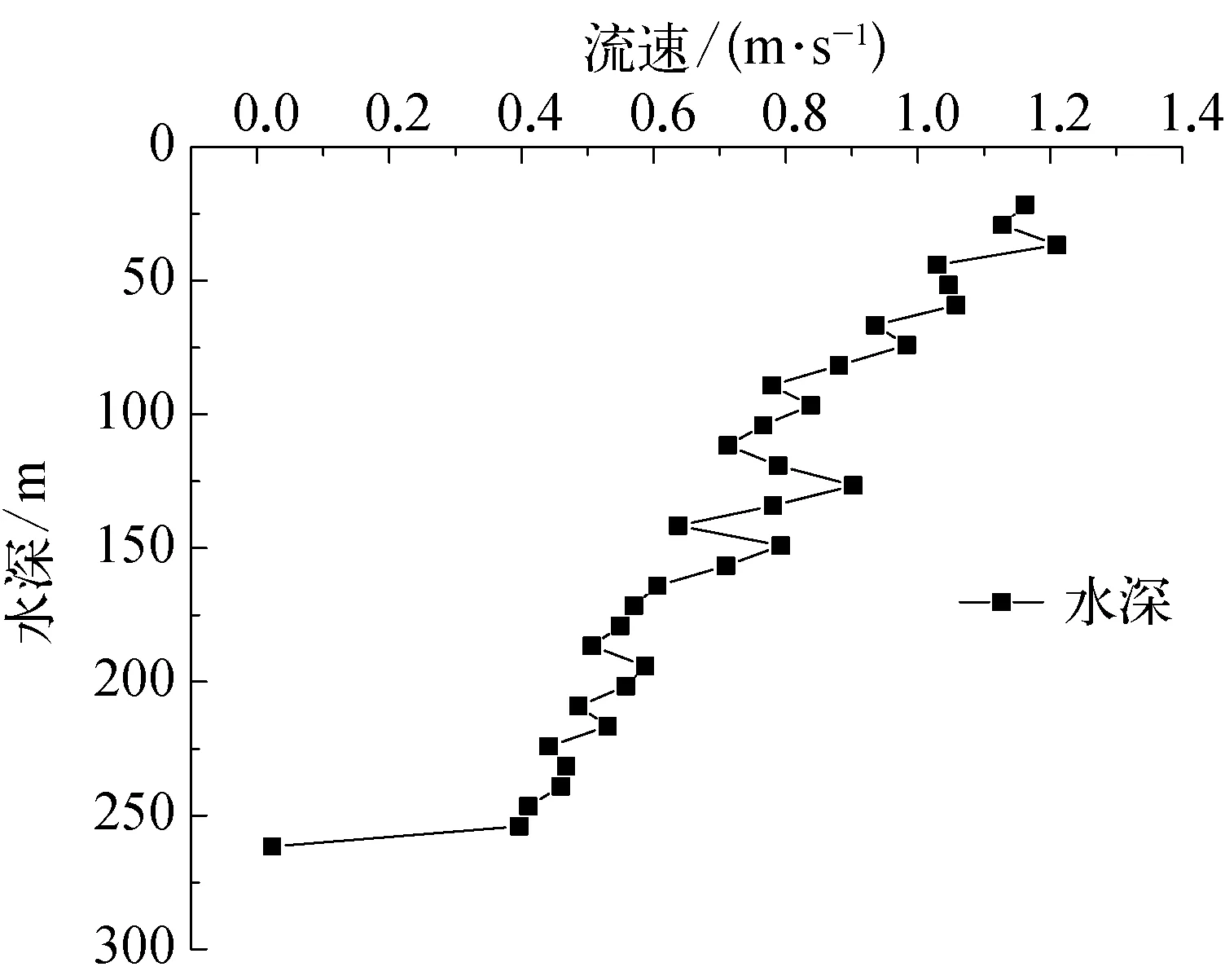
图2 流速剖面

在数千米的长距离水力垂直输运过程中，输运管道面临外部深海剪切流的直接作用，加之其底部处于自由悬垂状态，管道自身会绕其顶部连接位置产生一定的旋转，使得管道呈现复杂的空间构型，再叠加水面采矿船在海面二阶波浪力的作用下，会产生长周期的慢漂运动，使得整个输运管道载荷和运动呈现显著的低频特征。不难看出，长距离悬臂式输运管道在环境作用下会呈现非线性特征强烈的复杂力学性能[11-17]。

2.3 海洋环境条件

流速剖面见图2。

不规则波采用JONSWAP谱，目标谱公式：

(11)

计算用波浪工况见表3。

表3 波浪工况表

3 模型试验

试验模型由水面采矿船、长距离输送管道、输送软管和采矿车组成，模拟了完整的深海采矿系统。

模型试验在海洋深水试验池完成，缩尺比λ=1∶30，试验水深40 m，对应实际水深1 200 m。模型试验用的水面支持船模型见图3，水下部分模型见图4。

图3 深海采矿系统模型试验(水面船)

图4 深海采矿系统模型试验(水下管道)

由于本次试验研究的关注点在于管道的力学响应，因此模型试验设计时重点考虑了重力相似和弹性力相似，即主要根据傅汝德数相似以及柯西数相似准则进行模型相关参数的选取。

傅汝德数和柯西数相似要求模型与原型应满足以下关系：

(12)

(13)

式中:vf为流速，g为重力加速度，D为直径，ρ为流体密度，E为弹性模量。

试验具体参数见表4。

表4 试验模型参数

试验中，为测量长距离垂直输运管道的载荷情况，在管道顶部与水面船连接位置，从顶部向下1.36 m位置以及管道末端位置分别设置了3个三分力传感器。

4 结果与分析

4.1 长距离垂直输运管道载荷分布

图5和图6展示了长距离垂直输运管道的轴向张力和剪力沿管长的分布情况(以表3的A4工况为例)。

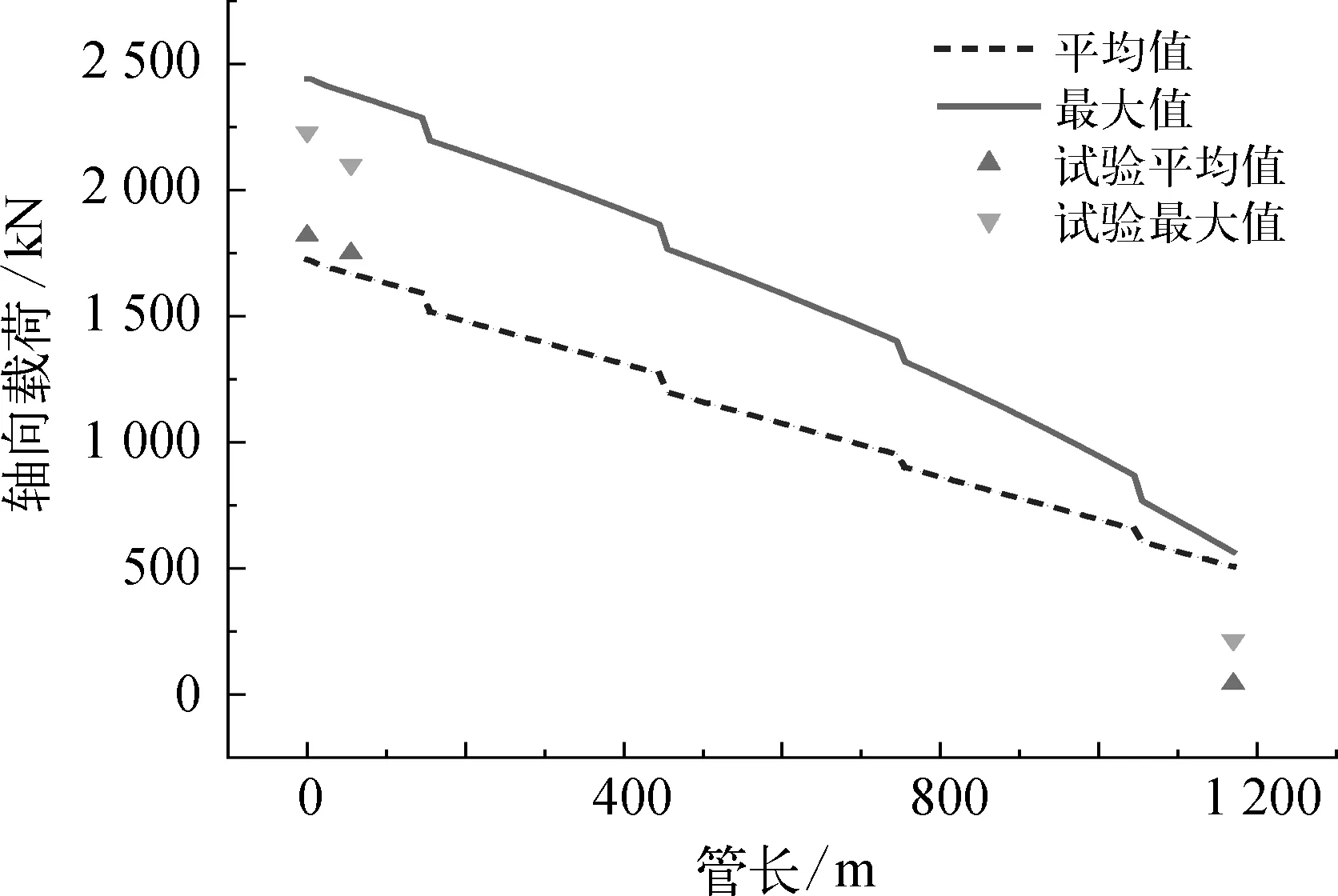
图5 管道轴向张力分布

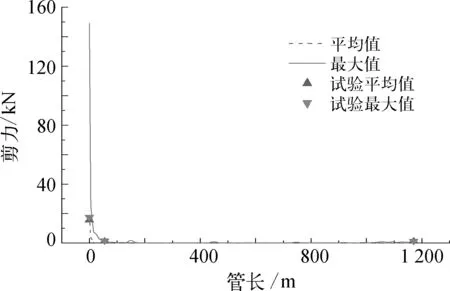
图6 管道剪力分布

数值结果是根据试验的模型参数按照相似准则换算后，导入数值计算软件计算得到的。管道的轴向张力和剪力的分布的数值计算的结果(包括管道载荷的最大值和平均值)在图中以曲线的形式呈现，同时为了便于对比，将模型试验中测量的三个管道的相应位置的时历结果进行统计之后，以点的形式呈现在图中。

由图5和图6可以看出，长距离垂直输运管道的轴向张力和剪力的极值均出现在管线的顶部位置，自上而下随着水深增加，载荷逐渐减小。其中，轴向张力变化趋势相对平缓；剪力在靠近水面的位置变化剧烈。此外，在全管长范围内，轴向张力显大于剪力，说明轴向张力在管道整体受力中占据主要地位。因此，下文后续讨论将以管线顶部位置的载荷作为重点。

4.2 海流作用载荷分析

海流对结构的影响主要分为两部分进行分析。首先讨论流速大小对于结构的影响，以图2中的流速剖面为基础，取该流速剖面的50%，75%，100%，125%，150%作为变量展开计算(即对图2中各深度的流速整体按比例进行放大或缩小)；接着分析流向角对结构的影响，取图2的流速剖面，同时将海流方向与艏向夹角作为变量，流向角分别取180°，135°，90°，45°和0°展开计算。结合计算结果和试验结果后发现：海流对于管线系统的影响主要体现在剪力上，对轴向张力响很小。图7和图8分别展出不同流速剖面下和不同流向角下的管道顶部位置剪力的变化情况。

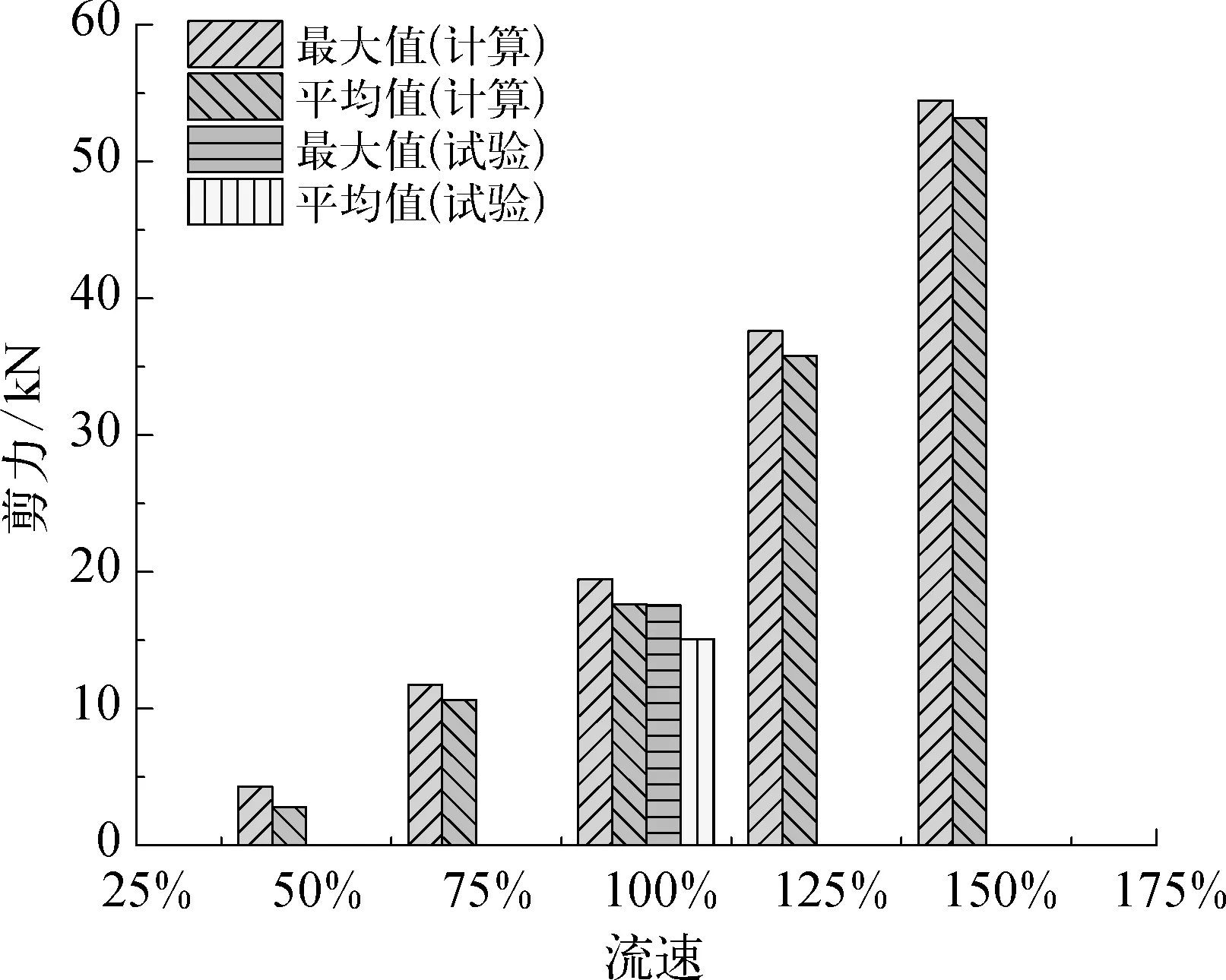
图7 海流流速对管道顶端剪力的影响

图8 海流流向角对管道顶端剪力的影响

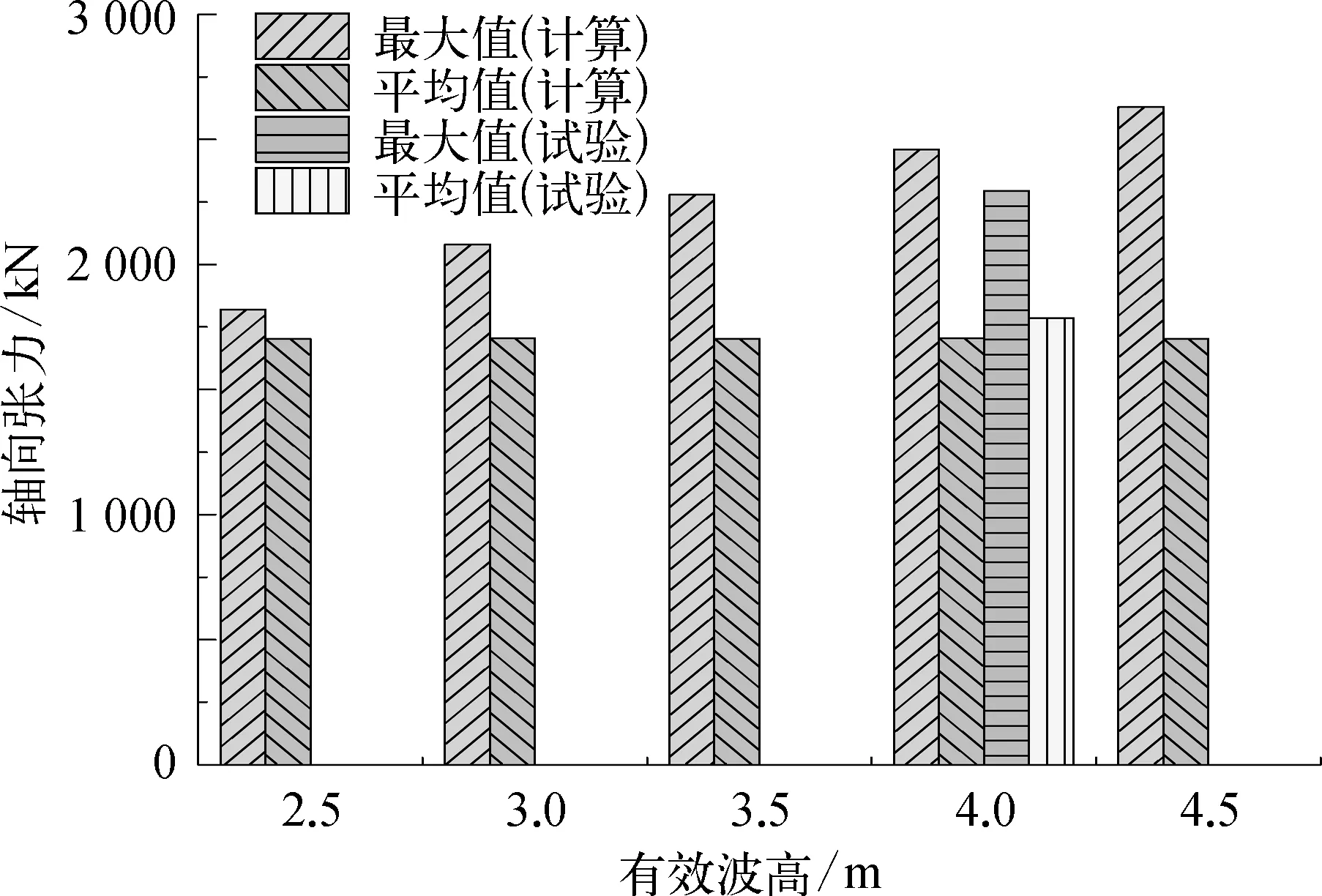
图9 有效波高对管道顶端张力的影响

由图7和图8可以看出剪力随着流速增加而增加，增幅明显；剪力随流向角变化幅度相对较小，流向角为90°时剪力最大，剪力平均值是180°时的145%，流向角为0°时的剪力比180°大；计算结果比试验结果偏大，计算最大剪力比试验值大10%，计算平均剪力相比试验值大17%。

4.3 波浪作用载荷分析

本节依次计算并分析了有效波高，谱峰周期和浪向角对于管道顶端载荷的影响，具体计算工况见表3。计算过程中注意到轴向张力远大于剪力，因此本节后续分析将以轴向张力为主。结合计算结果和试验数据后，计算结果见图9、图10和图11。

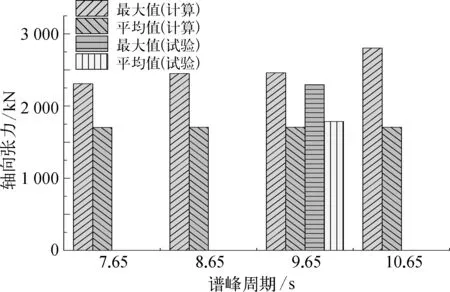
图10 谱峰周期对管道顶端张力的影响

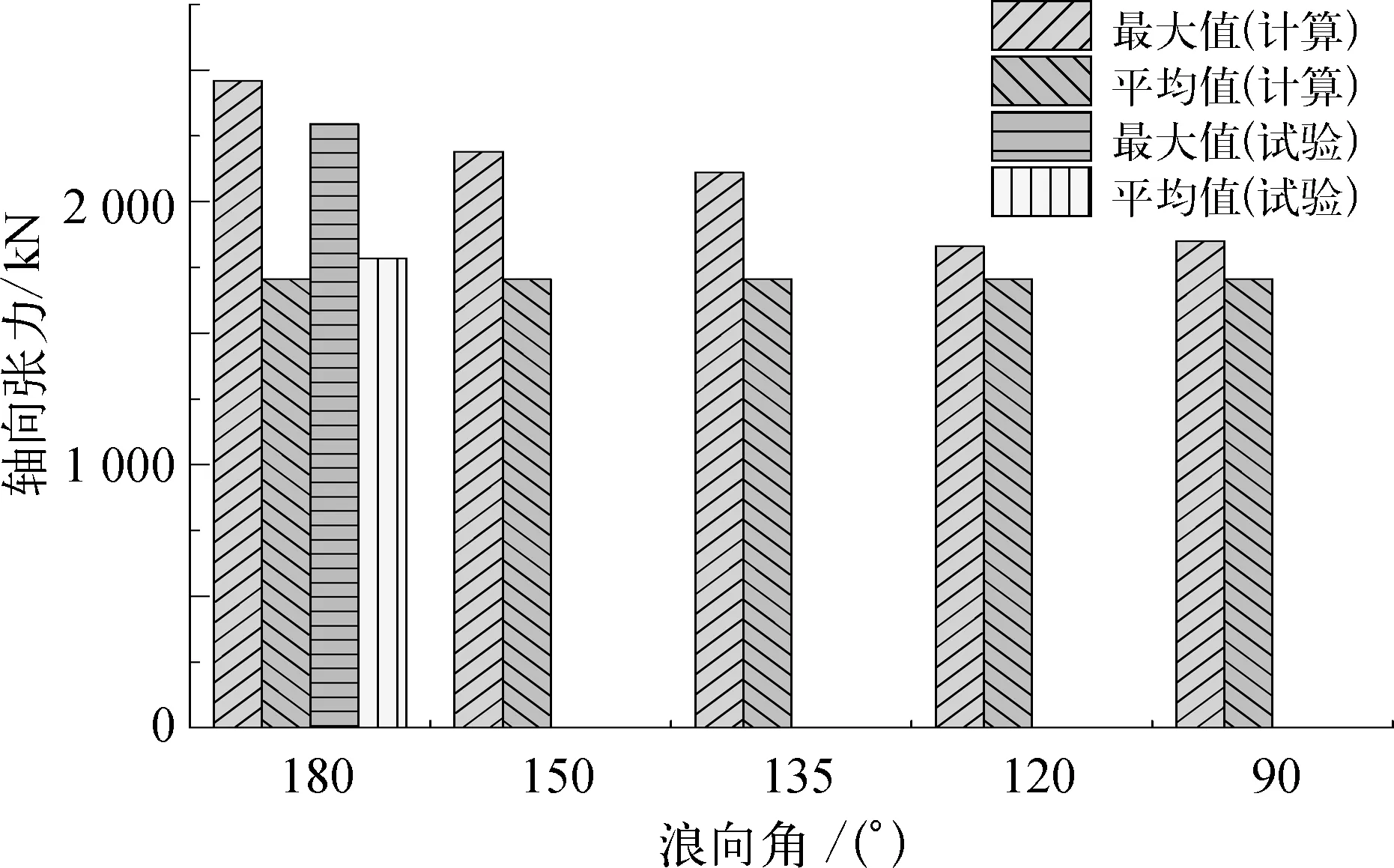
图11 浪向角对管道顶端张力的影响

综合图9～11可以看出，全计算工况下轴向张力的平均值保持稳定，可以认为轴向张力的均值主要由结构自重决定，受环境条件影响小。波浪参数对于轴向张力的最大值有明显的影响：随着有效波高和谱峰周期的增加，轴向张力最大值逐渐增加；浪向角从180°到90°的变化过程中，轴向张力最大值逐渐减小。全部计算结果中，轴向张力的极值和均值差距最大达到了48%，试验值差距为38%。数值计算结果和试验结果相比，轴向张力的平均值误差约为3%，最大值误差约为7%，可以认为计算结果与试验结果较为吻合，计算可信度高。

扬矿管的轴向张力与水面船的垂荡运动有着一定的关系，模型试验中，水面船最大加速度达到了1.63 m/s2。在这里一并给出了模型试验中水面船在波浪作用下的垂荡加速度时历曲线及其谱分析结果，见图12。

图12 水面船垂荡加速度

对于各工况中的管道顶端轴向张力时历曲线进行谱分析，有以下结果，如图13～16所示。

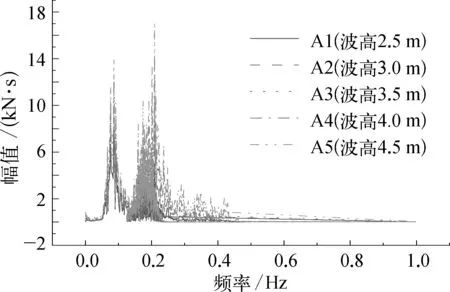
图13 轴向张力频谱(不同波高)

图14 轴向张力频谱(不同周期)

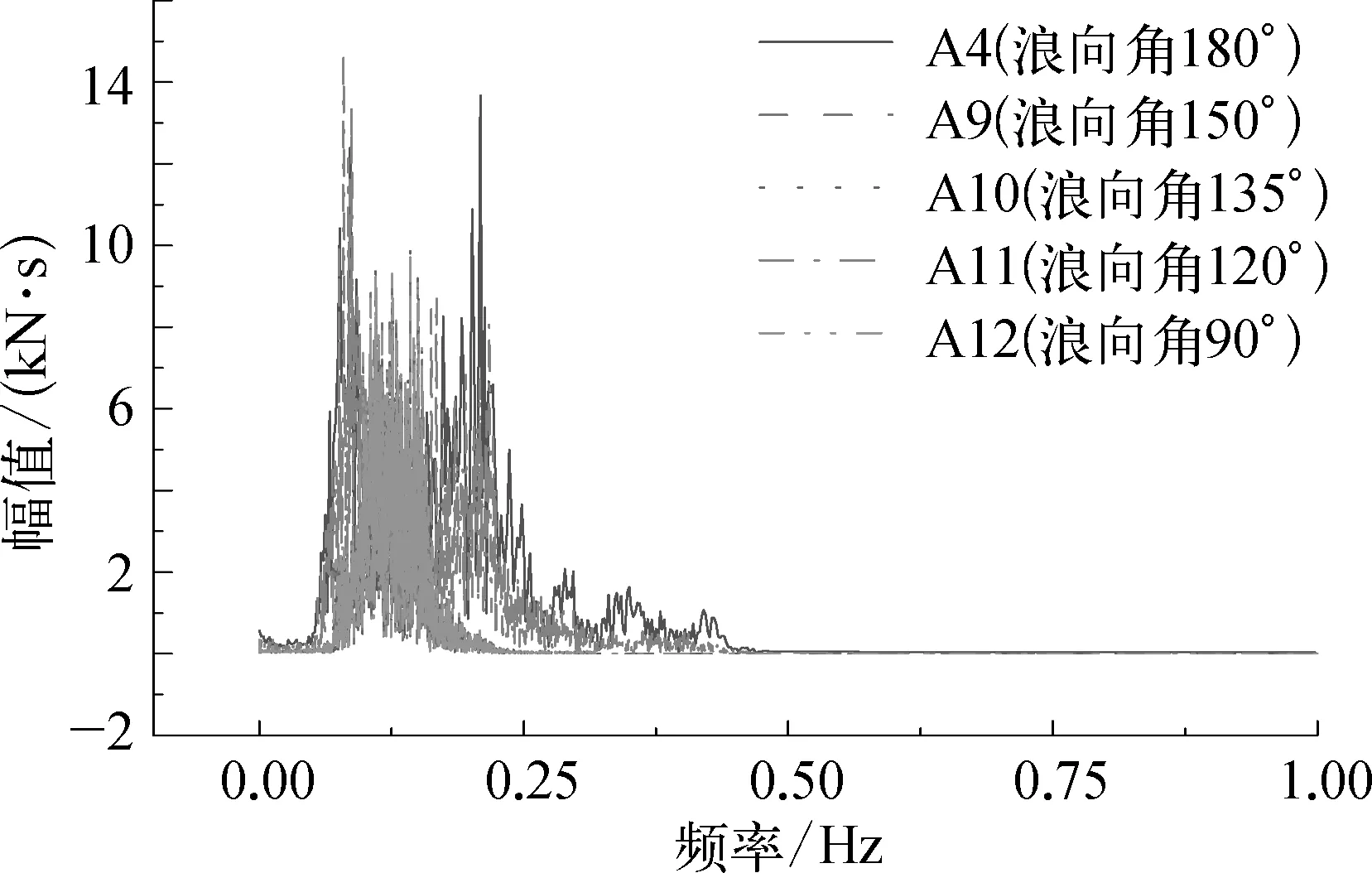
图15 轴向张力频谱(不同浪向角)

图16 轴向张力频谱(计算与试验对比)

由图13～16可以看出，波高对于频谱的幅值有一定的影响；整体幅值随着波高的增加而增加；谱峰周期对于频谱的谱峰位置有一定的影响，峰值位置随着谱峰周期变化而变化；浪向角对于频谱的整体幅值和峰值均有一定的影响；试验结果和数值计算结果相比，在频率为0.10～0.11 Hz位置的峰值位置基本重合，误差大约2%，相比试验结果，在频率为0.20～0.21 Hz的位置出现了一个次级的峰，且从图14中可以看出，随着浪向角的变化，两个峰的峰值出现了相对的变化，由此判断峰值的出现和水面船有一定关系。同时这个现象是试验结果中未出现的，推测是由于计算中模型发生了弹振现象[18-19]导致的。

4.4 浪流耦合作用载荷分析

计算分析了海流和波浪单独作用下的结构载荷后，进一步综合考虑浪流耦合作用下顶部位置的载荷情况。浪流耦合作用分析中，重点考虑不同波浪和海流角度组合对于结构的影响。

本节计算的流速剖面见图2，波浪取表3中的A4工况，计算时的浪向角从180°到90°间隔15°均匀取值共选取7个不同浪向角度，流向角从180°到0°间隔45°均匀取值共选取5个不同的流向角度。轴向张力的计算结果见图17。

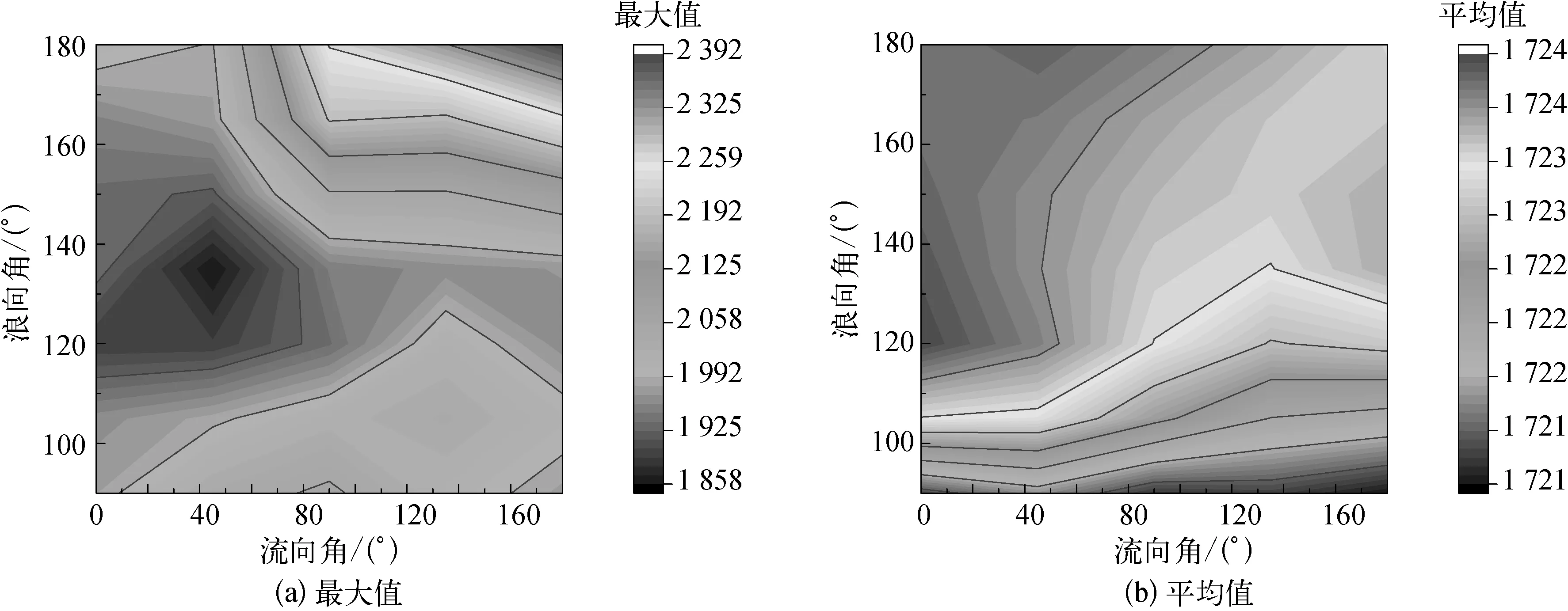
图17 顶部位置轴向张力

从图17可以看出：轴向张力的最大值在浪向角为135°，流向角为0°时取得极小值；在浪向角和流向角均为180°时取得极大值，极大值相比极小值增加了约33%；轴向张力的平均值在全计算域内变化很小，变化幅度约0.2%。

从图18中可以看出：剪力在浪向角为90°，流向角为180°时取得极大值，浪向角为120°，流向角为0°时取得最小值，总体来说随着浪向角从180°到90°变化过程中剪力最大值逐渐增加；剪力平均值在浪向角为90°，流向角为180°时取得极大值，在浪向角为180°，流向角为180°时取得最小值，平均值的变化趋势与最大值类似。

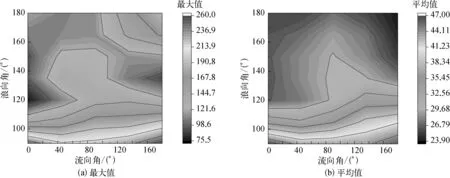
图18 顶部位置剪力

综合轴向张力和剪力的计算结果可以做出以下结论：顶部位置的轴向张力远大于剪力，在环境条件变化时，轴向张力有极值变化幅度大，均值稳定的特点。因此生产作业中建议将水面船的浪向角调整在120°～180°范围内，有利于减少结构载荷。

对于上述工况中的轴向张力时历曲线进行谱分析，结果如图19所示。

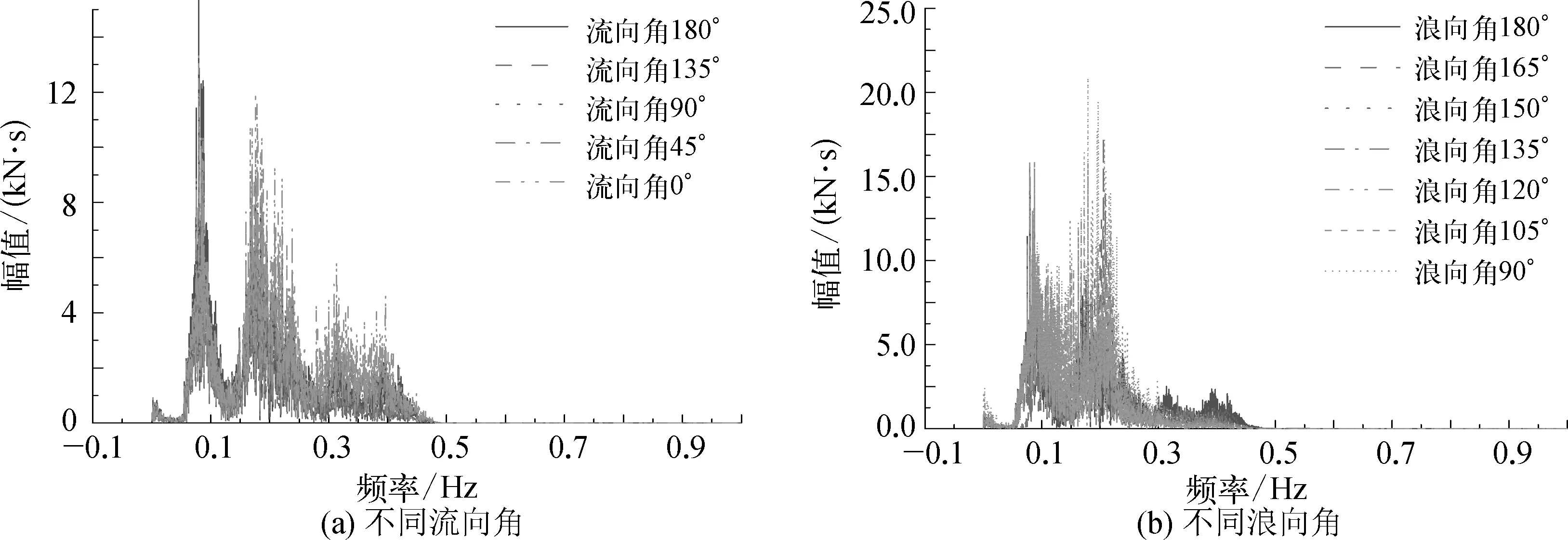
图19 轴向张力频谱

由图19可以看出：流向角变化对频谱几乎没有影响；浪向角对于频谱峰值有较大影响，浪向角从180°到90°变化的过程中，在0.1～0.2 Hz范围内幅值有一定增加，且峰值位置有从低频向高频变化的趋势。

4.5 安全系数计算以及对生产作业的建议

本节以数值计算结果分析结构的安全系数，对结构的安全性和可靠性作出评价，对工程应用提出建议。

在工程上，常使用Von Mises屈服准则来评价结构的安全性和可靠性，判断结构的应力是否达到了工程材料的屈服极限，作为其评价标准的Von Mises应力是基于剪切应变能的一种等效应力。Von Mises等效应力的计算公式：

(14)

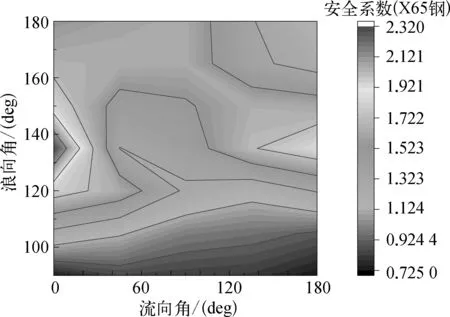
图20 结构安全系数计算结果

式中：σ1，σ2，σ3分别为第一、第二、第三主应力。

为评价结构安全性，以浪流耦合工况的计算结果为输入，进一步计算得到顶端位置的Von Mises应力。取Von Mises应力的最大值与管道所用材料的屈服强度进行比较(参考依据为X65钢，屈服强度555 MPa)。

从图20中可以看出，安全系数在流向角为0°，浪向角为135°时取得极大值，在浪向角为90°，流向角为180°时取得极小值；流向角一定时，浪向角从180°到90°变化过程中，安全系数先增加后减小在135°取得极大值。以安全系数1.5作为标准进行评判，可认为当水面船工作在浪向角120°～150°范围内时，结构具有较好的安全性能。

5 结 语

为了分析深海采矿系统长距离垂直输运管道在不同环境条件下的力学性能，采用数值计算和模型试验相结合的方式进行研究。首先分析了管道总体的轴向张力和剪力的载荷分布情况，并根据分布曲线将后续研究重点放在了顶部连接位置。后续设计了一系列计算工况，依次分析了海流作用，波浪作用及浪流耦合作用下结构载荷的变化规律，并将计算结果与试验结果相比较，验证了计算结果的可靠性。

通过以上的结果分析，可以清楚地发现：

1) 顶部连接位置的轴向张力远大于剪力，轴向张力极值受波浪作用影响有较大变化，张力均值主要由结构自重决定，不受环境条件影响；剪力的均值和极值受海流和波浪条件影响很大。

2) 数值计算结果和模型试验结果的拟合度好，数值计算模型可信度高。

3) 生产作业中应重点考虑轴向张力的变化，在顶浪或首斜浪的条件下作业；水面船在120°到150°的浪向角下作业时，管道系统有着较好的安全性能。