波浪作用下锚链系泊浮式防波堤动力响应的数值模型研究

金哲飞，张金凤, 2，张庆河，蔡 威，季超群

(1. 天津大学 水利工程安全与仿真国家重点实验室，天津 300072； 2. 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室(天津大学)，天津 300350；3. 中交第三航务工程勘察设计院有限公司，上海 200032)

波浪在传播过程中能量分布不均，其中98%的波能分布在距离水面三倍波高的水深范围内[1]。相比于传统固定式防波堤，浮式防波堤能够充分利用波能分布特性，在满足工程消浪要求的同时减少对工程水域水沙交换的影响。由于浮式防波堤具备施工快捷、拆卸方便、对环境适应性强且影响小等优点，在近岸工程中得到了较为广泛的应用[2]。

浮式防波堤的动力响应研究主要围绕消浪、透浪性能展开。在理论研究方面，Bouwmeester和Van[3]与Drimer等[4]分别基于线性波理论和二维势流理论对不同波况下单方箱浮式防波堤的透射系数计算进行了理论推导，Roul等[5]和何超勇等[6]在物理试验基础上对浮式防波堤透射系数公式进行了不同程度修正。物理试验方面，Uzaki等[7]和Sannasiraj等[8]分别通过改进浮堤形式、锚泊方式提升浮式防波堤消浪性能。侯勇等[9-10]通过改变浮堤相对宽度、相对吃水深度、锚链拖地长度、系泊角度等物理试验研究，分析总结了入射波周期、波高、水深、锚链系泊角度、拖地长度对浮式防波堤消浪性能的影响。

浮式防波堤运动过程受到波浪条件、浮堤结构形式、系泊方式等多种因素影响，经验公式难以准确计算其水动力特性，而物理模型试验操作复杂，成本较高。因此诸多学者提出不同数值算法对浮式防波堤水动力特性进行模拟。在波浪与浮式防波堤相互作用的数值模拟研究中，浮堤运动边界的流固耦合处理方法及锚链模型的选取至关重要。其中浮堤运动边界根据边界条件处理方式的不同，主要分为动网格变形、浸入边界、重叠网格法等。动网格方法适用于小幅度浮堤位移模拟，Ji等[11]使用分块移动网格建立二维双圆柱浮式防波动力响应数值模型，并利用物理模型试验验证模型在计算浮堤动力响应、锚链张力变化方面的准确性。王梦贤等[12]采用浸入边界法处理波浪与起伏板防波堤的耦合作用问题，开展规则波与起伏水平板防波堤相互作用的数值模拟研究。浸入边界法在三维问题中标志点的追踪较为复杂，在三维模型中使用较为困难。重叠网格法最早由Benek等[13]提出，具备网格生成质量高、适应刚体大幅度运动的特点，广泛应用于复杂结构物与流体相对运动的流固耦合问题求解。锚链张力模型建立主要基于动力学分析与静力学分析两方面展开。静力学分析中锚链张力的数值求解主要有分段外推法等。当忽略锚链拉伸变形及流场作用力，静力平衡方程退化为悬链线方程。缪泉明等[14]基于悬链线方程对于浮体动力响应采用六自由度运动方程求解，研究极限海况下浮体的动力响应及锚链受力，锚链张力峰值与实测结果存在较大差距。相比于静力学分析，动力学分析考虑锚链运动过程中所受的动力荷载，在锚链剧烈运动状态下缆绳锚链张力求解精度更高，锚链张力求解数值方法主要有集中质量法、节点单元法等。Vanden[15]采用集中质量法对锚链在动态响应下的最大张力进行了细致研究。Huang[16]将模型拓展至三维，更真实地模拟实际工况，提升计算精度。

基于OpenFOAM中olaFlow求解器，采用基于sugger++[17-18]重叠网格方法模拟箱式浮式防波堤动力响应，并在刚体六自由度运动求解过程中植入笛卡尔坐标系下MOODY锚链求解模块[19]进行耦合求解，锚链张力分析基于动力学平衡方程展开，采用间断有限元数值方法进行计算。建立链式结构浮体运动的二维数值模型，并通过试验对比验证模型计算的准确性。

1 波浪作用下浮式防波堤运动数学模型

1.1 基本控制方程

采用雷诺时均的Navier-Stokes方程(RANS方程)作为基本控制方程，其连续性方程及动量方程分别为：

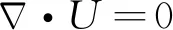
(1)

(2)

式中：U为流体速度；prgh为流体的修正压强(动水压强)，prgh=p-ρgh，p为总压强，ρgh为静水压强；ρ为流体密度；μeff为考虑分子动力黏性和紊流作用的有效黏性系数，μeff=μl+μt，μl为层流黏性系数，μt为紊动黏性系数，由紊流模型联合求解；C为流体表面张力系数，一般取C=0.07；κ为界面处曲率；α为VOF法引入的体积分数。

在求解RANS方程组时使用Menter[20]提出的SST k-ω两方程紊流模型闭合，自由液面采用Hirt和Nichols[21]提出的VOF(volume of fuid)法进行追踪捕捉。采用PIMPLE算法对压力泊松方程进行迭代求解。

1.2 数值波浪水槽

利用OpenFOAM中olaFlow求解器建立数值波浪水槽，采用速度入口造波，出流边界设置阻尼消波区，在该计算区域内动量方程在右端加入式(3)所示阻尼项求解[22]。

Sf=ρUθ(x)

(3)

(4)

式中：Sf为阻尼源项；θ(x)为阻尼系数函数；x为网格单元坐标值；x0为阻尼消波区起始位置坐标值，Lf为阻尼消波区长度；c为经验系数，取c=20。

波浪水槽底部边界为无滑移边界条件，顶部边界为压力边界。入流边界设置为主动吸收式速度入口造波边界，出流边界为消波边界[23]。侧边界为空边界。为减少计算网格，在水槽y方向利用OpenFOAM中extrudeMesh进行网格拉伸处理成单层网格。二维浮堤运动共分为3个自由度，分别为垂荡(Heave，沿z轴上下运动)，纵荡(Surge，沿x轴前后运动)，纵摇(Pitch，绕y轴转动)。浮堤运动计算采用六自由度运动方程求解，对其余三个自由度的运动进行限制，数值求解方法为Newmark算法。

1.3 重叠网格方法

为合理捕捉浮堤的运动过程，将浮式防波堤作为刚体处理，并采用重叠网格法进行模拟，如图1所示。该方法由划分固体的无变形贴体网格(虚线部分)、划分流场的背景网格(实线部分)两部分联合求解完成，网格中插值节点流场信息计算方程：

(5)

式中：φL为边界(边缘)节点的某一流场信息；αk为其对应的第k个插值贡献节点的插值系数；φk为对应第k个插值贡献节点的某一流场信息。

重叠网格中的贴体网格与背景网格分别建立在两套笛卡尔坐标系下，通过域连接信息(domain connectivity information，简称DCI)在背景网格与贴体网格间建立信息传递。计算时首先在贴体网格中寻找不参与计算的节点单元(洞单元，如图1黑点)，并分别在背景网格中寻找边缘节点(与洞单元相邻的计算节点)，在贴体网格中寻找边界节点(贴体网格中未被定义物理边界条件的计算节点)；在边界节点、边缘节点寻找合适的插值贡献节点并利用其位置关系求解插值系数；最后通过式(5)在两套网格中交换流场数据，并根据上一时间步浮堤运动调整贴体网格区域，重新建立DCI连接。

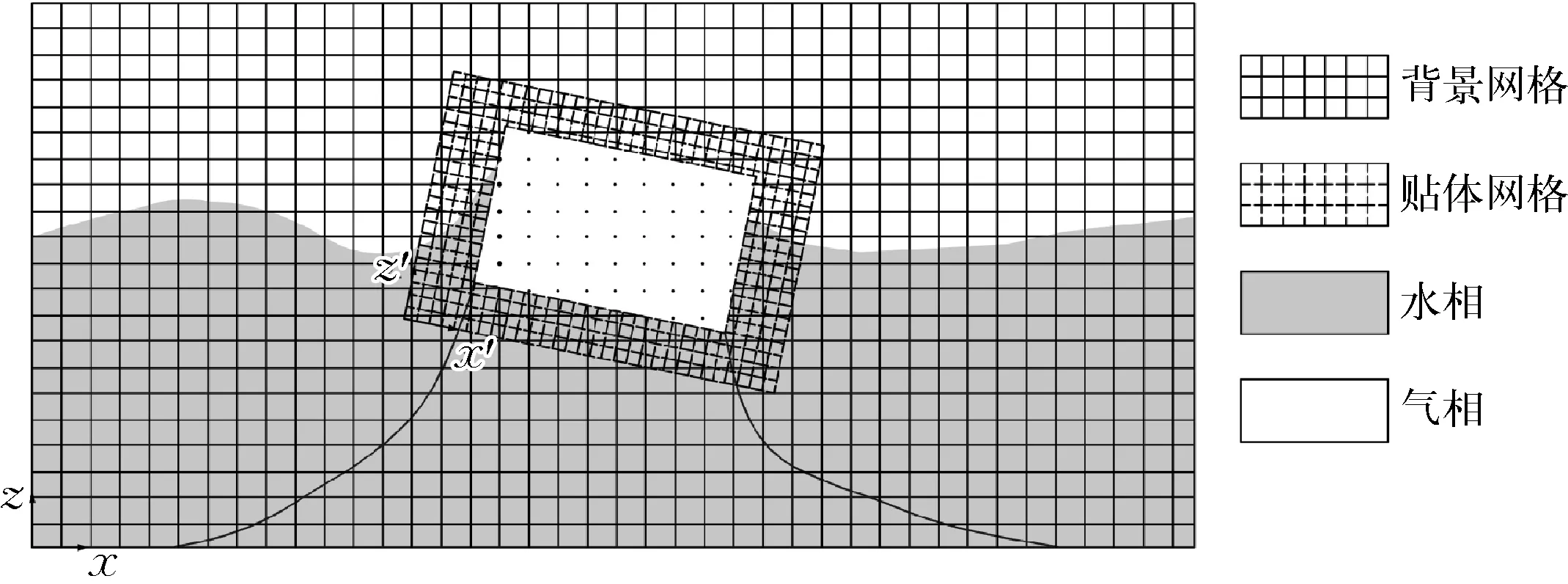
图1 背景网格与贴体网格组成的重叠网格系统

1.4 锚链求解模型

对于锚链受力计算部分采用节点单元法求解受力，在六自由度求解中耦合Palm开发的MOODY模块[19]。锚链的受力计算考虑悬空段所受流体的各项作用力及拖地段受海床面的作用力，忽略锚链弯曲刚度，并假定锚链质量不随时间发生变化。锚链在笛卡尔坐标系中的运动方程为：

(6)

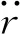
锚链在实际运动过程中应力—应变关系较为复杂。在受到波浪力冲击时锚链易产生较大张力，致使锚链单元应力—应变产生非线性关系。计算中假设锚链应力—应变关系遵循胡克定律[24]，始终处于弹性变形区[19]：

T=EA0ε

(7)

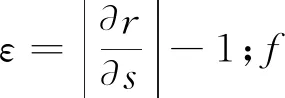
f=fa+fb+fc+fd

(8)

式中：fa为附加质量力，包括入射波产生的Froude-Krylov力；fb为浮力与重力的合力；fc为接触力；fd为黏性拖曳力。

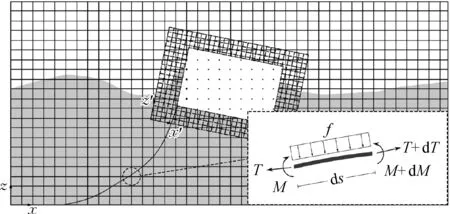
图2 锚链锚链节点受力示意

附加质量对锚链的动力学影响可分为：流体加速度引起的惯性力fa+和流体随锚链加速变化所引起的惯性力fa-两部分组成：

fa=fa+-fa-

(9)

根据Morison方程[25]，附加质量力分别从法向、切向两个方向计算：

(10)

(11)

式中：Ac为锚链截面面积；ρ为流体密度；U为流体速度；v为锚链速度；下标tan为速度的切向分量；CMn，CMt分别为法向、切向附加质量力系数。

浮力项的计算表达式为：

(12)

式中：ρc为锚链密度；γ0为锚链单位长度质量。

锚链尾端固定，其中拖地段与地面的接触力基于双线性弹簧和阻尼器进行计算，接触力项计算表达式：

(13)

(14)

(15)

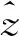
黏性拖拽力项根据Morison方程计算所得：

(16)

式中：CDt和CDn分别为切向和法向的拖拽力系数；v*为流体与锚链的相对速度；下标n为法向速度。

锚链求解采用间断有限元方法，对式(6)展开并在锚链域内进行空间离散。采用三阶Runge-Kutta对离散后的式(6)进行时间步递进，求出锚链单元节点的加速度、速度、位置信息，并更新单元节点张力。

1.5 浮堤运动求解过程

锚链力的求解通过修改OpenFOAM六自由度刚体运动求解顺序，植入基于节点单元法的锚链求解模块MOODY，并在六自由度计算过程中完成对锚链力的求解。植入MOODY模块后重叠网格刚体运动计算具体流程：

1) 流场初始化，建立重叠网格域连接信息(DCI)；

2) 根据DCI，进行网格插值计算；

3) 依据全场流场信息，调用MOODY模块求解锚链受力，并进行六自由度计算求解浮堤运动方程，对浮堤运动、锚链力耦合迭代求解，最后更新浮体周围流场信息，更新浮堤、锚链信息；

4) 更新贴体网格信息；

5) 根据更新的网格、流场信息，重新建立DCI；

6) 根据边界条件、上一时间步全场信息，PIMPLE迭代循环求解当前间步全场流场信息；

7) 进行新一轮迭代循环，直至残差符合要求进入新一时间步进行循环求解，或达到计算时长停止计算。

2 数值模拟结果

2.1 模型设置

数值模拟计算模型参照单方箱锚链式浮式防波堤水动力学特性试验，物理模型试验布置及各项参数如图3和表1所示,其余尺寸详见侯勇物理模型试验[9-10]。浮堤长(W)、高(H)分别为0.3 m、0.18 m，质量为17.82 kg。锚链物理参数、波高测点布置均与侯勇试验设置相同，锚链初始时刻拖地长度均为0。为避免造波边界对浮堤的影响，同时减少造波过程中的二次反射影响，数值波浪水槽造波边界与浮堤左侧之间距离设为4倍入射波长，出流边界附近设置2倍波长阻尼消波区，阻尼消波区距浮堤右侧2倍波长，其设置如图4所示。背景网格x方向长度取150分之波长，z方向取20分之波高。波浪水槽在y方向经过extrudeMesh拉伸成宽度为0.44 m的单层网格。

图3 物理模型试验示意

表1 模型及锚链各参数设置

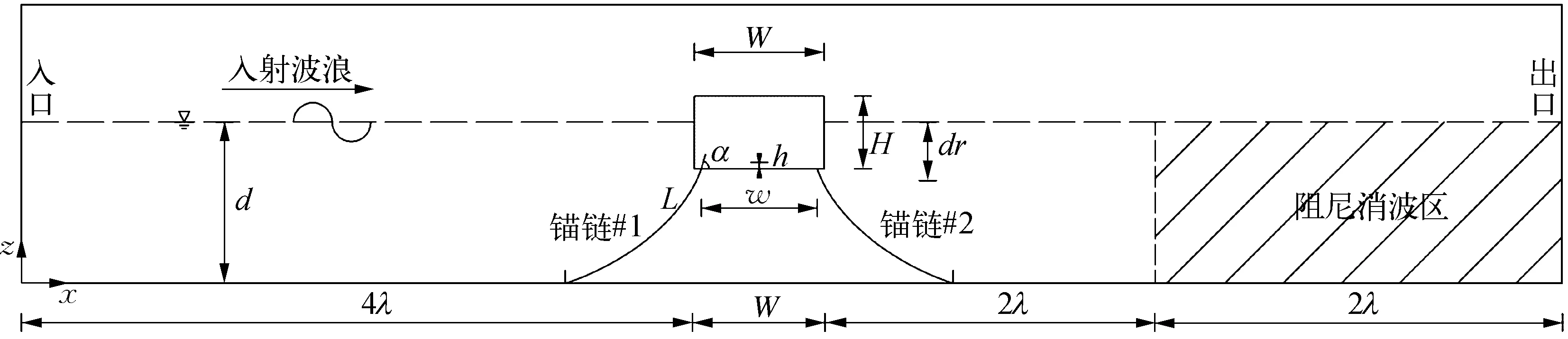
图4 数值波浪水槽断面示意

设置8组算例对二维锚链系泊浮式防波堤动力响应数值型进行验证，算例设置如表2所示。首先对数值波浪水槽进行空水槽造波校验。在未放置防波堤的数值波浪水槽中，提取预留浮式防波堤位置处(距速度入口边界4倍波长处)波高历时变化作为对比，计算时长为30倍波周期，图5以第二组波况为例显示了模拟结果与二阶Stokes波理论波面。由图5可知，波高变化在第20T以后渐趋稳定。表2列出了第20T～30T时刻波高均值与理论波高的对比情况，模拟结果与理论误差不大于2%，可以认为浮堤附近波高值达到算例设置波高值。

数值计算采用6块Intel Xeon E7 8870 v3处理器，每块处理器拥有18个核心，每组算例计算时长为10.23小时,CPU时长为10.21小时。8组对比算例中，选取相对宽度W/L、波高h，作为模拟工况的控制变量。选取各组第20T～30T周期浮堤透射系数(Ct)、纵荡(Surge)、垂荡(Heave)、纵摇(Pitch)、迎浪测浮堤系泊处锚链张力(F1)、背浪侧浮堤系播处锚链张力(F2)平均值与侯勇试验值进行对比。

图5 未放置防波堤的波浪水槽中x=4L位置处波高历时与波浪理论值对比(组Ⅱ)

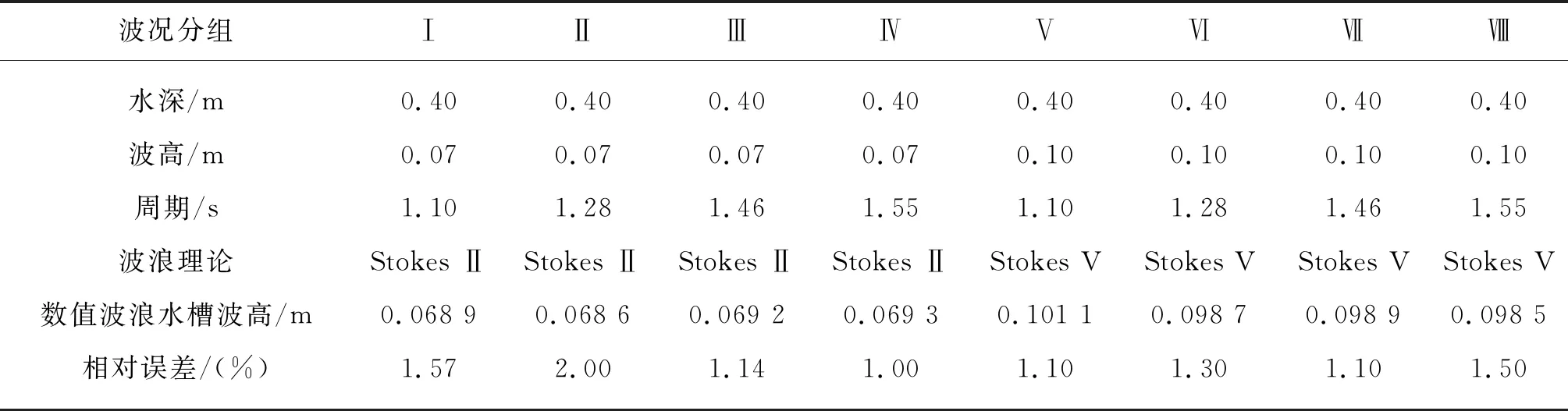
表2 波浪参数及数值模拟结果与理论解的比较

2.2 网格收敛性分析

在背景网格固定情况下，对组Ⅱ算例选取5种不同加密方式对贴体网格进行网格无关性分析，其中贴体网格最外层网格大小均为0.04 m×0.04 m，每级加密都对上一级加密中最靠近浮堤的四层网格尺寸进行减半。选取第20T～30T时刻垂荡、纵荡、纵摇峰值平均作为对比。从表3可以看出，当对贴体网格进行2级渐变加密时(图6)，浮堤纵荡、垂荡、纵摇均值计算结果与3、4级加密计算结果相差较近达到收敛，且计算耗时较短。因此选用2级加密方案(图6)对贴体网格进行局部加密。

表3 贴体网格收敛性研究

图6 贴体网格加密方案

2.3 浮式防波堤透射系数

计算结果分别提取图3中四个测点水面高度数据，并采用Goda两点法[26]消除堤前波浪反射影响，并计算透射系数，各组透射系数如图7所示,其中组Ⅳ两者相差最小，仅为1.2%；组Ⅴ相差最大，为10.72%。图7中各组透射系数均比侯勇物模试验值偏小，最大偏差发生在组Ⅴ，达10.72%。造成这种误差的原因可能与数值波浪水槽浮堤两侧无波浪透过，而物理模型试验浮堤两侧存在一定透水现象有关。

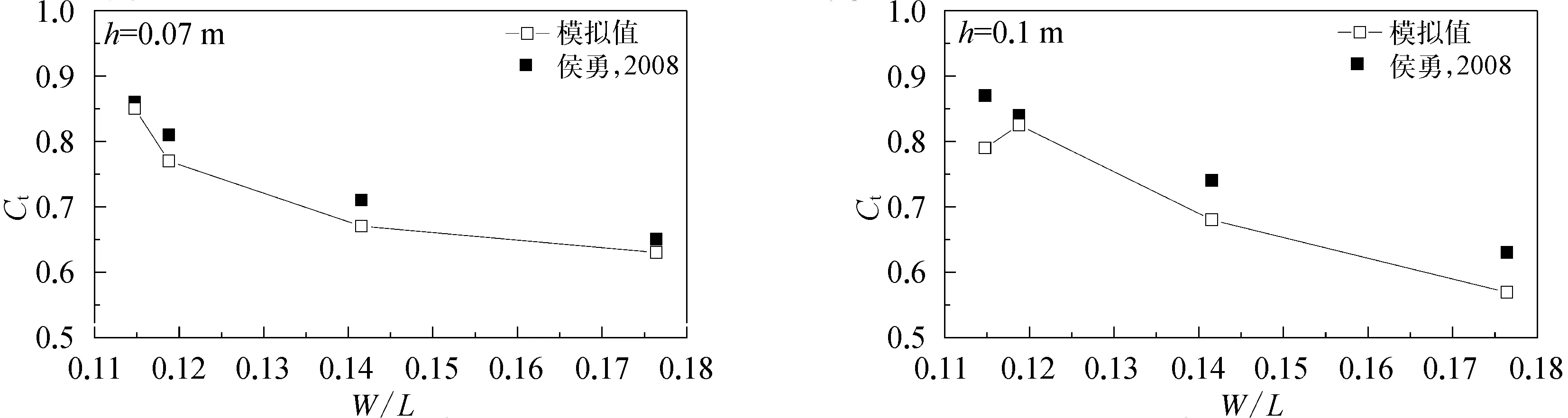
图7 各组透射系数(Ct)计算值与试验值对比

2.4 浮式防波堤动力响应

数值模拟试验中浮堤运动共三个自由度，分别为纵荡、垂荡和纵摇。图8以组Ⅱ为例显示了纵荡、垂荡和纵摇模拟计算结果。取第20T～30T周期浮块运动幅值平均值，并对三个自由度的振幅分别做无因次化处理，其运动特性通过响应振幅算子RAO加以描述：

(10)

式中：纵荡、垂荡和纵摇响应振幅算子RAO中的响应幅值分别取浮堤20T～30T时刻纵荡、垂荡和纵摇运动幅值均值，相应的响应算子单位分别为cm/cm，cm/cm，°/cm。

图8 组Ⅱ模拟历时

图9显示了组Ⅱ第28T各时刻浮堤运动响应。当波谷到达浮堤位置(t=0T)，浮堤垂荡达到谷值。随波浪传播垂荡、纵摇逐渐恢复至平衡位置，随后纵荡达到谷值，纵摇达到峰值(t=5/20T)。当波峰到达浮堤位置(t=10/20T)，浮堤纵荡、垂荡均达到峰值，纵摇接近平衡位置。波浪在浮堤迎浪侧形成反射造成浮堤纵摇出现次峰。随后浮堤垂荡再次回归平衡位置，纵摇到达谷值(t=15/20T)。当浮堤垂荡再次经过平衡位置(t=15/20T)，纵摇逐渐回归平衡位置，垂荡逐渐到达谷值(t=20/20T)。由图8可知浮堤的纵荡和垂荡基本与波面同相位，纵摇与波面相位相差约T/4。

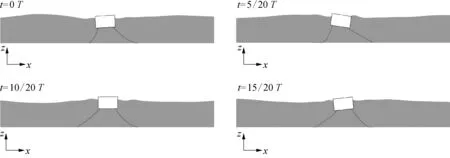
图9 组Ⅱ第28T(35.84～37.12 s)浮堤运动响应

图10显示了不同工况下浮堤运动响应振幅算子与侯勇试验值的对比情况，两者偏差最大者为组Ⅶ垂荡响应振幅算子，为10.44%；组Ⅳ纵荡响应振幅算子模拟与试验值偏差最小，为0.6%。总体而言，模拟结果与试验结果吻合较好。

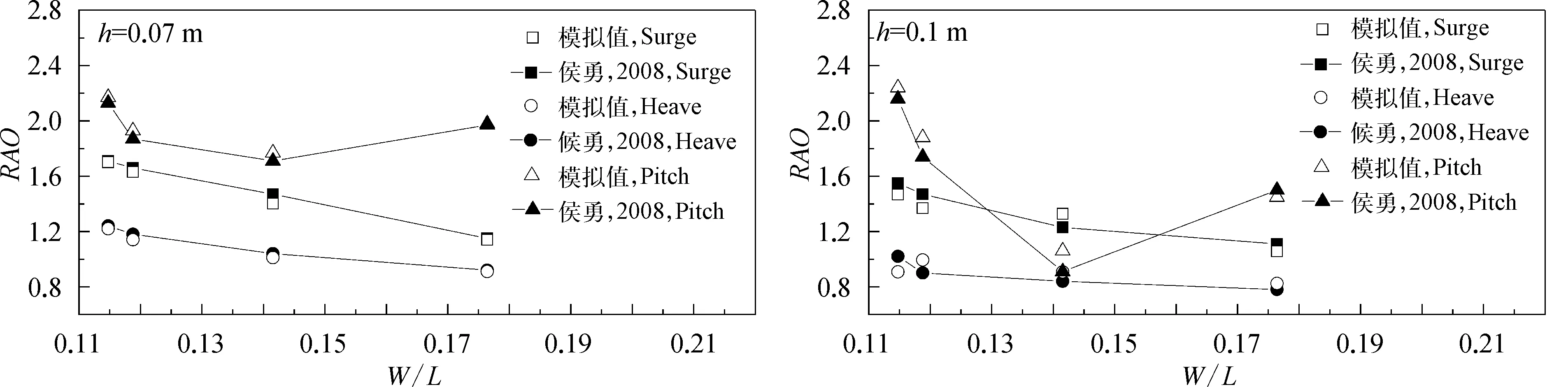
图10 响应振幅算子模拟值与试验值对比

2.5 锚链张力

模拟结果取锚链-浮堤连接端节点张力值作与试验结果进行对比。图11为组Ⅱ锚链张力变化历时曲线。浮体动力响应呈稳定周期性变化后(20T)，迎浪侧锚链张力(F1)第20T～30T周期平均峰值为40.12 N，背浪侧锚链张力(F2)平均值为29.85 N。迎浪侧与背浪侧锚链张力峰值交替出现，且迎浪侧锚链张力峰值更大。

图11 组Ⅱ锚链张力历时曲线

图12为浮堤锚固处锚链张力振幅算子与试验值对比(侯勇试验值无组Ⅳ，Ⅶ，Ⅷ)，误差最大为21.8%(组Ⅰ背浪侧)，最小为2.8%(组Ⅱ迎浪测)。锚链背浪侧张力模拟和试验值的偏差相对较大，其原因可能与浮堤运动响应过程中背浪侧锚链松弛时间更长(图9)，拖地段锚链与海床的接触力模拟误差较大，且锚链在张紧瞬时受冲击峰值存在一定震荡现象相关。模拟中当锚链拖地段运动速度达到0.1 m/s时到达静摩擦最大值并近似认为进入滑动摩擦阶段，滑动摩擦力不变。实际锚链运动时拖地段地面接触力变化比模拟设置条件更加复杂。此外，模拟中对于锚链的应力—应变本构模型采用了线性化假设，在锚链承受剧烈冲击荷载时，应力—应变关系与实际情况存在一定偏差。

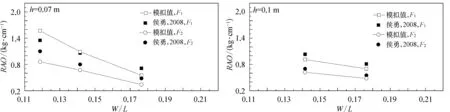
图12 锚链张力计算值与试验对比

3 结 语

基于OpenFOAM中olaFlow求解器，利用重叠网格在计算过程中适应刚体大幅运动的优势，采用重叠网格方法模拟浮堤动力响应，并在刚体运动求解过程中植入笛卡尔坐标系下MOODY锚链求解模块进行耦合求解，建立锚链系泊浮式防波堤动力响应的二维数值模型。浮式防波堤锚链尾端在海床中固定，因此在数值模拟中可简化成MOODY锚链模型进行锚链张力的求解计算。数值模型通过侯勇物理模型试验进行对比，并分别验证透射系数、浮堤运动响应、锚链张力峰值模拟结果。

在透射系数对比中，由于数值波浪水槽在y方向对网格进行了拉伸处理，相比物模试验不存在入射波从浮堤两侧透过的情况，因此透射系数模拟值整体偏小(误差为1.2%～10.72%)；在浮堤运动响应方面，垂荡、纵荡、纵摇运动响应模拟误差在0.6%～10.44%；由于锚链拖地段与海床接触力基于双线性弹簧和阻尼器进行求解计算，实际锚链受力更加复杂，因此背浪侧锚链张力峰值模拟误差部分达到21.8%(组Ⅰ背浪侧锚链张力)。此外，模拟中锚链应力-应变模型采用了线性化假设，在浮堤动力响应剧烈、锚链受到瞬时冲击荷载较大时，应力-应变关系存在一定误差。

通过数值模型模拟结果，该模型在计算波浪作用下锚链系泊浮式防波堤动力响应中具有比较高的模拟精度，可用于锚链材料应力-应变模型改进，浮式防波堤三维数学模型开发、浮堤消浪性能评价与结构优化计算。