聚焦波浪在浅堤上传播变形高精度数值模拟研究
易振宇,蒋昌波, 2, 3,屈 科, 2, 3,邓 斌, 2, 3,陈 杰, 2, 3
(1. 长沙理工大学 水利工程学院,湖南 长沙 410114; 2. 水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114; 3. 洞庭湖水环境治理与生态修复湖南省重点实验室,湖南 长沙 410114)
近年,极端波浪造成的海洋灾害事件频发。据统计,从1954至1982年的28年中,在全世界范围内,极端波浪直接造成了至少36座石油钻井平台的翻沉[1]。同时,资料记载在1969至1994年间,至少有22艘大型舰船由于遭遇极端波浪而失踪[2]。由于受全球气候变化和海平面上升的影响,极值波浪发生的频率和强度都有所增加[3],而近岸区域是人类活动最为频繁的区域,所以开展极端波浪与近岸建筑物的相互作用研究是非常重要的。
极端波浪现场观测难度大,现场观测资料少,因此试验和数值模拟成为研究极端波浪产生及演变机理的重要手段。研究发现,波浪聚焦是产生极端波浪的重要机理之一,不同频率的波浪在传播过程中相互作用,波能集中,最终形成极端大波,此过程称为波能聚焦。由于聚焦波浪具有随机波浪的性质,比较符合实际的海况,因此许多学者采用聚焦波浪来模拟极端波浪的产生[4-6]以及对海岸结构物的破坏机理[7-9]。其中,Baldock等[4]通过开展试验工作,系统研究了大量波浪通过聚焦产生瞬态极端波群的机理,并且基于线性波理论,采用叠加规则波的方式实现了波浪聚焦,并引入了群的概念,研究了非线性波-波相互作用对单向波群结构的影响。Westphalen等[5]讨论了数值波浪水槽中极端聚焦波群的产生机理和传播特性,并对极端波浪的非线性效应进行了分析。Ning等[6]对聚焦波群的演变和水质点运动进行了试验和数值研究。对于聚焦波浪与结构物的相互作用,国内外许多学者也进行了研究。Buldakov等[7]采用二阶摄动理论分析了聚焦波群对底端固定的直立圆柱的绕射作用。Bai等[10]建立了高阶边界元模型,采用混合的欧拉-拉格朗日法对数值波浪水槽内直立圆柱与完全非线性规则波和聚焦波作用导致的波浪传播和绕射情况进行了模拟及分析。Walker等[11]基于线性势流理论并利用NEWWAVE方法开展了极端波浪与多柱体结构的模拟研究。庞红犁[8]对极端波浪作用下结构物的高频共振效应进行了分析研究。卓晓玲[9]应用高阶边界元方法,对水流中聚焦波浪的演化过程进行了数值模拟,并研究了波浪频谱宽度和直墙摆放位置等参数对聚焦波与直墙相互作用下的压力分布以及波浪爬高的影响规律。
为防止极端波浪对海岸结构物造成破坏,人们在海岸周围修建了海岸防护工程。其中浅堤作为一种常见的护岸建筑物,得到了大量的应用。浅堤可以导致波浪提前破碎,阻挡和减弱波浪的作用力,从而达到保护海岸结构物、防止海岸侵蚀的目的[12]。研究浅堤周围波浪演变过程及流动结构是分析浅堤消浪机理的基础。从20世纪90年代开始,许多研究人员为研究浅堤的消波特性开展了大量的物理模型试验和数值模拟研究。Beji等[13]针对波浪通过梯形浅堤的水动力学过程开展了详细的物理模型试验,他们发现了波浪通过浅堤时产生的高频能量现象。通过分析波浪变形及破碎等现象建立了相应的数学模型。Koraim等[14]研究浅堤对海堤上的波浪爬高、波浪反射及传播变形的影响。结果表明,随着相对浅堤高度和相对浅堤宽度的增加,浅堤的波浪透射系数逐步降低。Cho等[15]通过开展物理模型试验研究系统分析了透水及不透水矩形和梯形浅堤的波浪反射系数,并指出梯形浅堤对入射波的反射能力优于矩形浅堤。范海荣等[16]分析了规则波和不规则波通过梯形浅堤时波浪外部形态变化以及内部能量变化规律,并探讨了周期、波高、淹没深度等要素对浅堤周围波高与能量的影响。除此之外,Chang等[17]利用PIV技术对孤立波通过矩形浅堤上的流场进行了详细的测量与分析。除了开展物理模型试验研究,许多学者采用不同的数值模型对浅堤周围波浪的传播特性进行了系统研究。Ohyama等[18]基于时变边界元法(the time-dependent boundary element method)数值分析了非线性波列通过浅堤时的分解现象。结果表明,波浪通过浅堤时大量的波能向高频转移,且透射波的能量谱不仅受入射波频谱本身的影响,受入射波各分量相位差的影响更大。Losada等[19]采用基于雷诺平均Navier-Stoles(RANS)的数值模型模拟了梯形透水浅堤附近的流场分布和波浪变形,与实验室水槽试验结果吻合良好;李昌良等[20]基于二维RANS方程和VOF方法,模拟了波浪在多种不同结构形式的浅堤上的传播,并从流场结构和波能耗散角度,提出了最优的浅堤结构形式。在实际工程中,单浅堤有时不能满足消浪要求[21],许多学者还对双浅堤的消浪效果开展了研究。如Cao等[22]试验研究了相对淹没水深、相对防波堤间距等因素对双梯形浅堤波衰减特性的影响。Liang等[23]使用非静力波浪模型SWASH(simulation waves till shore)对双梯形浅堤上波浪传播进行了数值模拟,并详细研究了防波堤间距和水流对波浪传播的影响。
前人虽然针对浅堤上的波浪传播特性开展了大量的物理模型试验和数值模拟研究,但是关于极端波浪在浅堤上的传播鲜有研究。罗洵等[24]采用Boussinesq波浪模型,分析了聚焦波在对称梯形浅堤上的非线性传播变形。陈勇等[25]利用试验及自主研发的CIP模型(constraint interpolation profile model)模拟了极端波浪在浅堤上的传播,并分析了流场特性。但以上研究均未讨论波浪要素对聚焦波在浅堤上传播特性的影响。
因此,基于开源程序REEF3D,建立二维高精度数值波浪水槽,系统研究各波浪要素对聚焦波在不可透浅堤上传播特性的影响。由于浅堤的堤顶水深是波浪在浅堤上传播变形的最重要的影响因素之一[14,23,26],首先探讨在不同堤顶水深情况下透射波高以及波浪能量变化规律,然后在恒定堤顶水深条件下,研究聚焦波的聚集点与浅堤的相对位置对聚焦波通过浅堤传播变形的影响。此外,还考虑了双浅堤布置对聚焦波传播变形的影响。
1 数学模型
1.1 控制方程
采用REEF3D求解非定常两相不可压缩流动,控制方程为雷诺平均N-S方程,具体表达式:
(1)
(2)
其中,m和n可取1和2,U1和U2分别代表x方向和z方向的速度,x1和x2表示水平和竖直方向的坐标,ρ是流体密度(ρair=1.205 kg/m3,ρwater=998.2 kg/m3),P为压强,g为重力加速度,ν是层流运动黏性系数(νair=1.41×10-5m2/s,νwater=1.004×10-6m2/s),νt是涡黏性系数。
本研究采用了k-ω两方程湍流模型[27]计算涡黏性系数,湍动能k和湍流耗散率ω可以通过下面的控制方程求得:
(3)
(4)
其中,cμ=0.09,cω1=5/9,cω2=5/6,σω=σk=2,|S|2由应变张量的平均速率构成:
(5)
采用高精度的Level-Set方法[28]分辨水气交界面,其通过求解对流方程,得到流场,控制方程为
(6)
其中,φ(x,t)需满足关系式:

(7)
采用五阶加权WENO格式[29]数值离散速度对流项,这种高阶格式提供了建立复杂自由表面流动模型所需的精度,并且由于其非振荡特性而具有数值稳定性。Jiang和Peng[30]提出的WENO格式被采用对level set函数φ、以及求解湍流动能k和湍流耗散率ω的输运方程进行离散。时间推进采用三阶TVD性质的Runge-Kutta方法[31]。为了满足计算稳定性的要求,采用满足Courant-Friedrichs-Lewy(CFL)条件的自适应时间步长,本文所有计算,CFL数均设定为0.1。REEF3D采用均匀的网格离散计算区域,并且采用浸没边界法GCIBM(a ghost cell immersed boundary method)[32]处理复杂的计算边界。
1.2 聚焦波浪的产生
采用Jacobsen提出的松弛造波方法[33],将整个计算区域分为造波区、工作区和消波区,如图1所示。数值波浪水槽在造波区内通过将波浪解析解和数值解进行距离加权拟合生成波浪,并且采用同样的方法在消波区内吸收波浪,具体方法可参看文献[33]。
聚焦波是通过线性波分量在空间和时间的预定点上叠加产生的[34]。自由表面η(1)的表达式为
(8)
其中,Am是每个波分量的波幅,θm是每个波分量的相位,采用下面的公式计算
θm=kmx-ωmt-εm
(9)
εm=kmxF-ωmtF
(10)
其中,km、ωm分别为波分量的波数和圆频率。εm组成波分量的相位角,对于非规则波,εm是0到2π之间的一个随机数。对于聚焦波,εm使得每个波分量在指定的聚焦时间tF和聚焦点xF上聚焦。
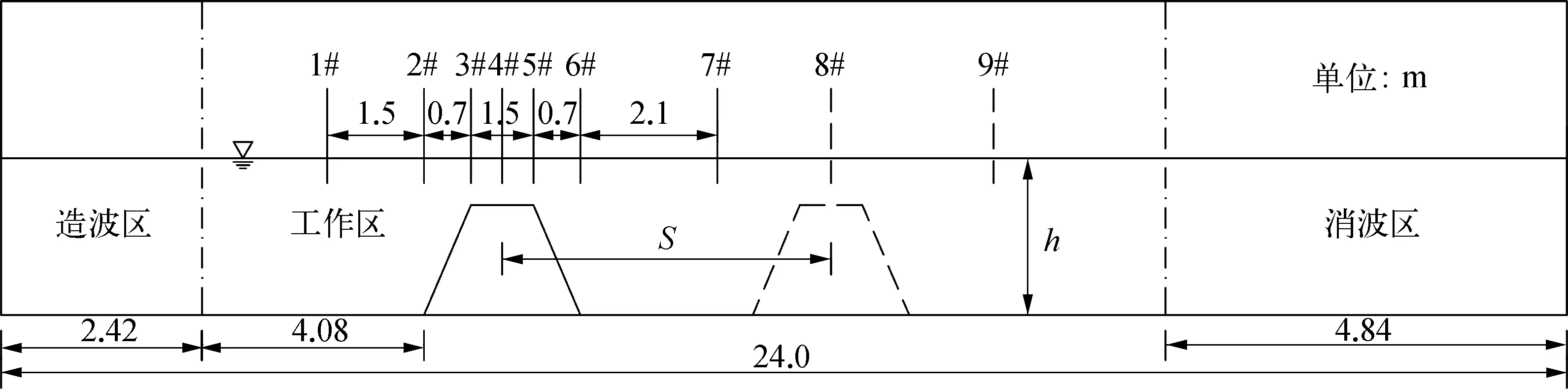
图1 数值波浪水槽布置示意
2 模型验证
2.1 聚焦波造波能力验证
为了验证数值波浪水槽生成聚焦波的能力,首先数值模拟了聚焦波的生成与传播过程,并且将计算结果与Ning等[6]的试验数据进行了对比。Ning等[6]在长69 m、宽3 m、高1.5 m的水槽中开展了相关试验研究。试验静止水深设置为0.5 m,聚焦点设置在距离推波板11.4 m处。这里设定的计算区域长度为24 m、高1.0 m。为验证网格无关性,共采用了三套计算网格,网格分别率分别为:粗网格(dx=0.05 m)、中网格(dx=0.025 m)、细网格(dx=0.01 m)。为节约计算时间,数值计算中将聚焦点设置在7.5 m和7.2 m处,聚焦时间设置为10 s,具体参数设置见表1。

表1 聚焦波参数设置
图2给出了聚焦点处计算水位与试验测量水位时程曲线对比。从图2(a)所示的水位对比中可以看出本文所采用的数值模型能够准确预测聚焦波的产生和传播过程。同时对比三套网格的计算结果可以看出,粗网格的计算结果与试验数据相差较大,而中网格和细网格均可以得到较为准确的计算结果。计算所得到的聚焦波波型和聚焦时间均与试验测量结果较为吻合。因此,细网格的网格分辨率可以满足网格无关性的要求,下面的算例都采用细网格(dx=0.01 m)进行计算。对于AF=0.087 5 m情况,由于较高的非线性影响,聚焦点发生了后移,图2(b)给出了给定聚焦位置xF=7.2 m和实际聚焦位置xFa=8.5 m处的波面高程与试验数据对比,结果表明实际聚焦位置处的自由面高程与试验数据吻合较好。

图2 聚焦点处数值模拟水位与试验数据对比
2.2 规则波在浅堤上传播变形的验证
目前关于聚焦波浪在浅堤上传播变形的试验研究鲜有发表。基于聚焦波可由多组规则波在给定的时间和位置叠加形成,为验证本文数值模型计算聚焦波浪在浅堤上传播变形的能力,模拟了规则波在梯形浅堤上传播变形的水动力学过程,并将计算结果与Ohyama等[35]的试验数据进行了对比,试验布置如图1所示。初始静止水深设置为0.5 m,入射波周期T为1.34 s,波高H为0.05 m。设置水槽最左端为坐标原点,波浪传播方向为x轴正方向,浅堤堤脚处坐标为x=6.5 m处,浅堤前坡坡度和后坡坡度均为1∶2,堤顶宽度为1.5 m。在单浅堤工况条件下,共设置7个测点采集波浪水槽的波面高程数据。图3给出了测点5、7处水位的计算结果与试验数据的对比。从图中可以看出,随着水深的逐渐减小,波峰逐渐变陡,波谷逐渐变平,计算得到的波峰略低于试验观测值(图3(a))。尽管如此,数值计算结果与试验数据整体吻合较好,进一步验证了本模型计算波浪在浅堤上传播变形的能力。

图3 规则波通过浅堤时测点处水位计算结果与试验数据的对比
3 聚焦波浪在浅堤上传播变形的模拟
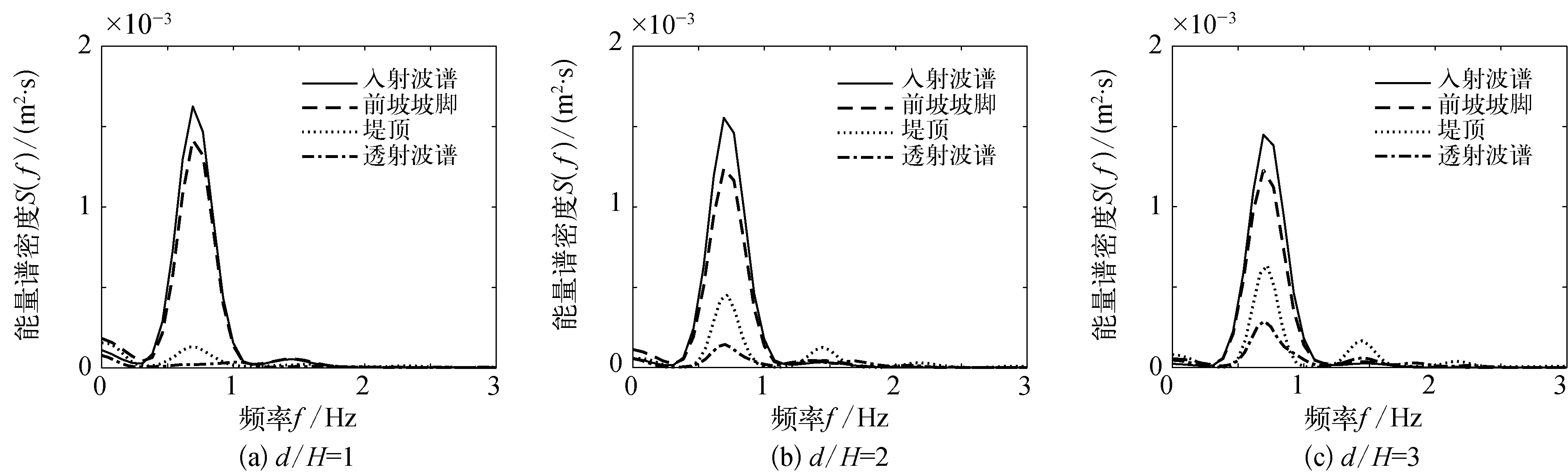
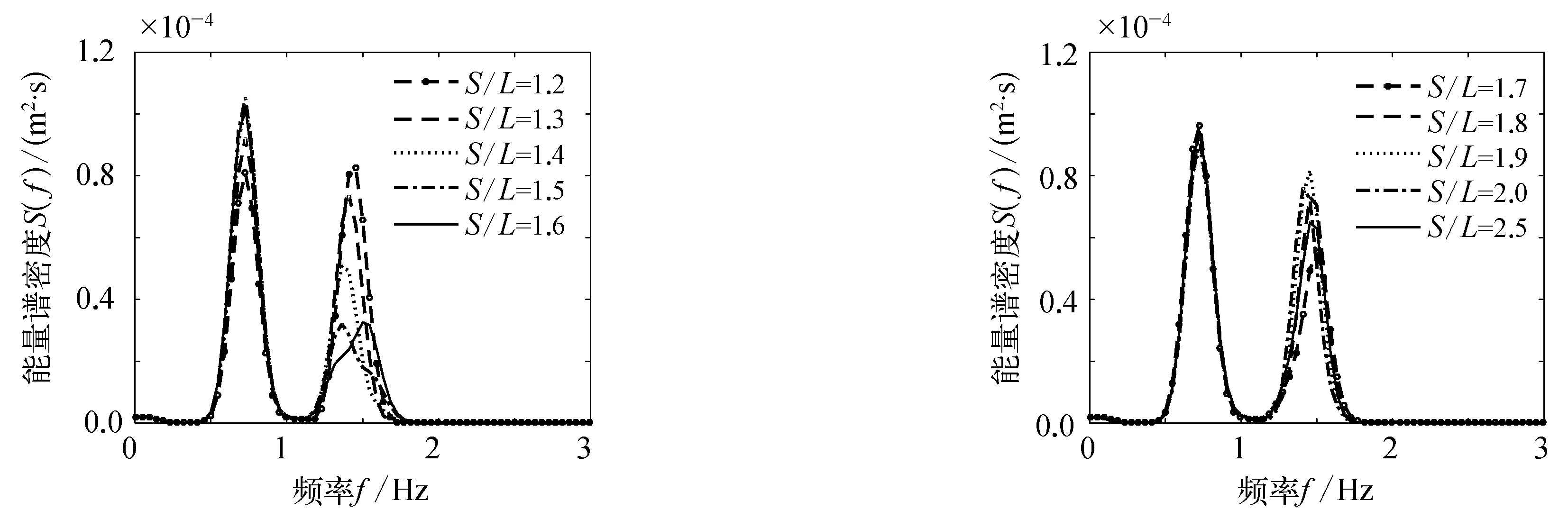
采用数值模拟方法,系统研究聚焦波浪在浅堤上的传播变形过程,着重分析了聚焦波浪通过不可透浅堤的水动力过程及能量变化规律,讨论不同波浪要素对聚焦波浪传播特性的影响,并且考虑双浅堤布置对聚焦波浪传播变形的影响。计算区域的设置与2.2节中相同,如图1所示。当波高比较大时,波浪之间存在显著的非线性干扰,波浪真实的聚焦点位置会发生后移[34],所以在研究聚焦波浪在浅堤上传播变形过程之前,需要确定波浪真实的聚焦位置和聚焦时间。采用AF=0.025 m和AF=0.075 m两种聚焦波幅的聚焦波进行研究,波频范围均为0.57 Hz 图4 聚焦波在不同时刻和不同位置的波面最大值 从图4中的计算结果可以看出,在聚焦波幅AF=0.025 m时,聚焦波波面在初始设定的聚焦点位置(t=8.0 s、x=6.5 m)达到最大值;当聚焦波幅为AF=0.075 m时,由于存在非线性的干扰,实际聚焦点后移到x=7.0 m处,实际聚焦时间为t=8.2 s。 在确定了实际的聚焦位置和聚焦时间之后,通过改变堤顶相对水深和设定不同的浅堤位置,研究在堤顶淹没深度和聚焦点与浅堤相对位置对聚焦波传播特性的影响,具体工况设置如表2所示。在研究双浅堤对聚焦波传播特性的影响时,通过固定上游浅堤位置,移动下游浅堤来改变双浅堤的间距(工况设置如表3所示),试验共设置9个测点采集两个浅堤堤顶处和浅堤前后的波面高程数据(如图1)。 表2 聚焦波通过单浅堤算例设置 表3 聚焦波通过双浅堤算例设置 对聚焦波浪在浅堤上的传播变形过程进行了研究,其中水深为0.5 m,聚焦波幅为AF=0.025 m(Case1)。图5为浅堤存在与不存在时不同测点处波面随时间的变化过程。聚焦波在未到达浅堤前,两种情况下的波形基本吻合(x=5.0 m),且均在聚焦点处(x=6.5 m)达到最大波高,波峰两侧的波形成对称分布,说明聚焦波波形基本不受浅堤反射影响。随着聚焦波的传播,相较于浅堤不存在时的对称波形,浅堤存在时,波浪的浅化作用增强,聚焦波的波峰逐渐变尖陡,波谷则变得平坦,同时波浪不对称性增强。聚焦波波高在后坡坡顶处(x=8.7 m)达到最大值,且相位与浅堤不存在时的相位错开。越过堤顶之后,水深变深,波峰开始变得平坦,波高逐渐减小且逐渐趋近于浅堤不存在时的聚焦波高。聚焦波越过浅堤之后(x=11.5 m),水深不再发生改变,但波高逐渐减小且低于浅堤不存在时的聚焦波高。在该聚焦波幅条件下,聚焦波浪经过浅堤未发生破碎。 图5 聚焦波在无浅堤和有浅堤水槽中传播变形 浅堤的堤顶水深是影响波浪在浅堤传播变形最重要的因素之一,为此,许多学者研究了相对堤顶水深对波浪通过浅堤时透射系数的影响[14,23,26]。本节系统研究相对堤顶水深(堤顶水深d/聚焦波高H),对聚焦波浪通过浅堤传播变形以及波浪能量转换的影响。浅堤堤脚设置在实际聚焦点x=6.5 m(Case1、2、3)和x=7.0 m(Case4、5、6)处,前坡坡度和后坡坡度均为1∶2,浅堤堤顶水深d分别取0.05 m、0.10 m、0.15 m(水深h=0.4 m、0.45 m、0.5 m),即相对堤顶水深d/H为1、2、3。 图6 不同相对堤顶水深条件下的各测点处波面极值 图6给出了聚焦波幅为AF=0.025 m时,不同相对堤顶水深的条件下,不同测点处(见图1)的波面极值。从2#点可以看出不同相对水深的聚焦波浪都会聚焦在设置的聚焦点处,当波浪沿着浅堤前坡向上传播,波浪的非线性逐渐增强,由于浅化作用,波峰增大。在相对堤顶水深为1时,沿程波面最大峰值出现在前坡坡顶位置3#,且浅堤后的波面极值相对于其他两种堤顶水深情况最小,说明在该堤顶水深情况下浅堤对波浪的衰减效果较好。随着相对堤顶水深的增加,沿程波面的最大峰值沿堤顶往下游移动,当相对堤顶水深较大时,变形后的聚焦波最大波面极值出现在后坡坡顶5#(x=8.7 m)。在相对堤顶水深为1和2时,波浪发生了破碎。上述的聚焦波在浅堤前和浅堤堤顶以及浅堤后的波面极值变化说明波浪能量在频域上有很大改变,除了能在波浪外部形态特征体现以外,浅堤对聚焦波的影响还体现在波浪能量的变化上。为了分析聚焦波浪通过浅堤时的能量变化规律,通过快速傅里叶变换(FFT)算法得到了上述波浪序列的频谱变化图(见图7)。 图7和图8显示了三种不同相对堤顶水深条件下,浅堤前后不同位置处的能量谱密度。当聚焦波传至浅堤堤脚处时,谱峰频率为0.75 Hz。聚焦波沿浅堤向上传播,受到浅堤浅化作用的影响,波能由低频处向高频处非线性转换,从而产生与基波传播速度相同的高次谐波,同时谱峰值有所减小。到达浅堤后坡时,随着水深逐渐增大,高次谐波释放为自由波,波浪的频散性导致不同频率的谐波以不同的速度传播,出现明显的次峰,波谱明显由单峰谱过渡到双峰谱。可以看出,相对堤顶水深越小,波能衰减的越多。在相对堤顶水深为1时,波浪沿程衰减效果最好,在聚焦波幅较小时(AF=0.025 m),堤后透射波主频能量降低到入射波主频能量的10%左右,在聚焦波幅较大时(AF=0.075 m),堤后透射波主频能量降低的更多。当相对堤顶水深增大到3时,波能衰减较少,但波能相对集中。从三种堤顶水深频谱变化图可以看出,浅堤的存在,一方面使主频能量减少,另一方面促使波能由低频处向高频处转化,从而加速波能的衰减,且浅堤的存在对大波幅的聚焦波能量衰减的更多。 图7 不同相对堤顶水深条件下的聚焦波频谱变化图(AF=0.025 m) 图8 不同相对堤顶水深条件下的聚焦波频谱变化图(AF=0.075 m) 图9 不同浅堤摆放位置条件下的各测点处波面极值 在堤顶水深不变、聚焦点位置固定的条件下,研究聚焦点与浅堤相对位置变化对浅堤消波特性的影响。7个测点(坡前1#、前坡坡脚2#、前坡坡顶3#、堤顶中心4#、后坡坡顶5#、后坡坡脚6#、浅堤后7#,布置图见图1)与浅堤保持相对位置不变。图9比较了五种不同工况条件下(具体工况设计见表2中Case1、Case7、Case8、Case9、Case10),7个浪高仪位置处出现的波面极值。各个工况下的聚焦波波高均在后坡坡顶(5#)处达到最大,这表明最大波高出现点位置随浅堤移动而发生改变,并且与浅堤相对位置保持不变。同时由于水深的浅化作用,聚焦波在浅堤爬坡过程中的波面极值逐渐增大,聚焦波达到堤顶后,波面极值继续增大,且堤顶前半段(从3#到4#)的增长幅度大于堤顶后半段(从4#到5#)。波浪越过堤顶后,水深增大,聚焦波波面极值急剧减小。当聚焦波经过堤脚后,波面极值继续减小。在五种不同工况下,聚焦波传播经过浅堤后(7#)的波面极值差异较小,说明浅堤相对位置变化虽然对聚焦波在浅堤上的传播变形过程具有一定的影响,但对浅堤的消波效果影响较小。 图10给出了不同浅堤位置情况下,聚焦波浪通过浅堤时波浪频谱变化图。从图10中可以看出,当浅堤前坡坡脚放在聚焦点处时(图10(b)),由于聚焦后的波浪随着水深持续减小,波浪浅化作用增强,使波浪能集中。而在其他工况条件下,前坡坡脚和堤顶处的能量谱密度峰值以及透射波谱峰值都小于入射波谱峰值,且聚焦波通过堤顶后出现次峰,浅堤后的次峰峰值大于堤顶处的次峰峰值。随着浅堤坡脚与聚焦点的间距增大,堤顶处和堤后的波浪频谱变化不明显,进一步说明浅堤与聚焦点相对位置变化对聚焦波浪能量衰减影响不大。 图10 不同浅堤摆放位置条件下的聚焦波频谱变化过程 为分析浅堤间距对聚焦波传播的影响,开展双浅堤数值模拟研究。计算布置如图1所示,S表示浅堤间距,即浅堤堤顶中心线之间的距离。两个浅堤尺寸一致,浅堤高度、堤顶宽度、斜坡坡度分别为0.35 m、1.5 m、1∶2。在计算中堤顶水深均设置为0.15 m,聚焦波幅设置为0.025 m,浅堤相对间距S/L从1.2变化到2.5,具体参数设置如表3所示。在相对堤顶水深保持不变(d/H=3.0)的情况下,通过分析典型代表位置x=18 m(9#)处的能量谱变化,研究浅堤相对间距变化对波能转换的影响,从而确定最优浅堤间距,为工程实践提供参考。 图11 不同间距条件下的透射波谱变化过程 图11为浅堤相对间距S/L从1.2变化到2.5时x=18 m处的波浪能量谱密度。聚焦波浪越过浅堤时,波形发生改变,波浪能量从低频处传递至高频处,由原来的单峰谱变成双峰谱。当相对间距S/L从1.2变化到1.6,从基本频域处转移至高频处的能量减少,能谱形状也由强双峰谱转变成弱双峰谱,不对称性增强。当相对间距S/L从1.7变化到2.5,下游浅堤对上游浅堤的影响减弱,能谱形状随着相对间距的增大均呈现强双峰谱形,且不同间距下,波能转换基本相似。以上分析说明浅堤间距设置在合理范围内(S/L=1.6)有利于加强浅堤周围水体的紊动强度,消耗更多的波浪能量。但是随着浅堤间距的进一步加大(S/L>1.6),这种效果则越来越不明显。 基于开源程序REEF3D,建立二维高精度数值波浪水槽,系统研究聚焦波在浅堤上的传播变形及能量变化规律。主要结论总结如下: 1) 文中建立的二维高精度数值波浪水槽模拟计算了聚焦波浪在恒定水深情况下的传播过程,以及规则波在浅堤上的传播变形过程,计算结果与试验观测数据进行对比表明本模型有较强计算能力及稳定性; 2) 通过分析相对堤顶水深和聚焦点与浅堤相对位置对聚焦波传播变形的影响,得到在给定相对位置条件下,相对堤顶水深越小,浅堤对聚焦波的衰减效果越显著;在给定的相对堤顶水深条件下,浅堤位置对聚焦波浪的衰减作用影响不大。 3) 当聚焦波通过双浅堤时,部分波浪能量从低频转移到高频,且不同间距下波谱在低频段和高频段都具有相似的形状。随着浅堤间距的增大,下游浅堤对上游浅堤的影响逐渐减弱,转移到高频段的波能也逐渐减少,基本频域内的波能几乎不变,但小于单浅堤的透射能量。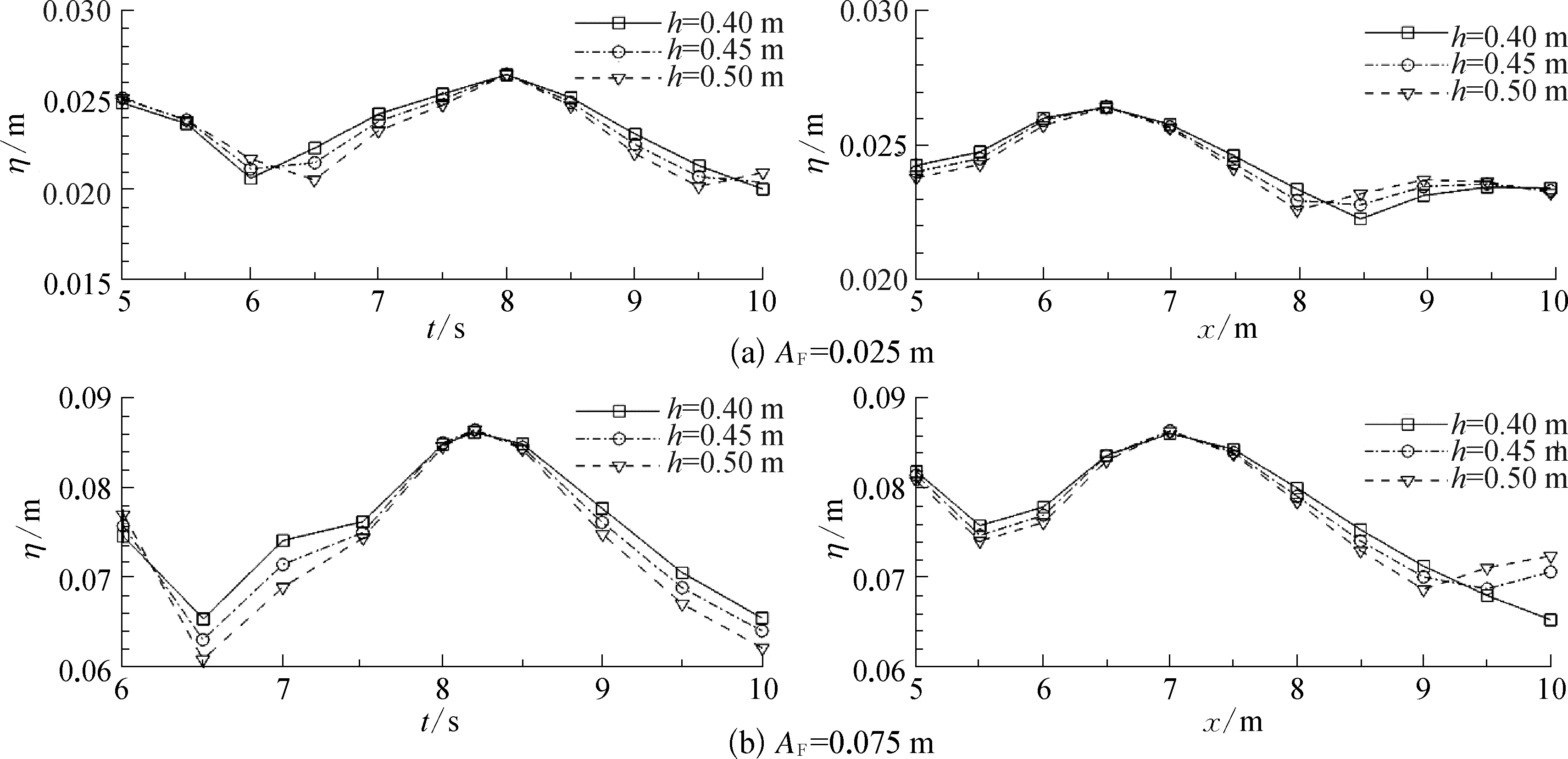


3.1 聚焦波在浅堤上的传播变形

3.2 相对堤顶水深的影响


3.3 聚焦点与浅堤相对位置的影响


3.4 双浅堤间距的影响
4 结 语

