海洋绞车主动升沉补偿控制系统建模与仿真分析
谢天财,黄良沛, 2,邹东升,陈 磊,刘德顺, 3
(1. 湖南科技大学 机电工程学院,湖南 湘潭 411201; 2. 湖南科技大学 机械设备健康维护湖南省重点实验室,湖南 湘潭 411201; 3. 湖南科技大学 海洋矿产资源探采装备与安全技术国家地方联合工程实验室,湖南 湘潭 411201)
海洋绞车是安装在海洋工程船舶上用于提升和下放设备的重要海工装备,在船舶补给转运、海洋管道铺设、海洋石油钻探等领域有广泛应用[1]。安装海洋绞车的母船在海流、波浪的影响下会上下起伏,将导致吊放设备与船体之间产生碰撞,影响正常水下作业和吊放设备水下作业精度[1]。为了减少波浪起伏对海洋绞车海上作业的影响,提高海洋绞车工作安全可靠性及水下设备作业精度,开展海洋绞车升沉补偿[2-6]系统理论及关键技术研究具有重要的理论意义和工程应用价值。现有的升沉补偿系统研究的载体多为钻井设备、钻柱等,且补偿系统大多采用半主动补偿系统。如黄鲁蒙等[7]设计了一种半主动式海洋钻井绞车升沉补偿系统。Cuellar等[8]提出了一种液压气动式补偿器和半主动控制方法。Quan等[9]提出了一种由被动和主动系统组成的半主动补偿系统。张萌等[10]建立了并联和串联两种形式的半主动式钻柱升沉补偿装置力学模型。上述文献所述的补偿系统多为半主动式补偿系统,而涉及以海洋绞车为载体的主动升沉补偿系统的研究则较少。为了更加贴切升沉补偿控制系统实际的工作环境,以不同海况下的波浪函数作为海洋绞车主动升沉补偿系统的外部激励,研究系统在不同海况下的补偿特性,使研究更切合实际,分析结果更有意义。
1 海洋绞车主动升沉补偿系统建模
1.1 主动升沉补偿系统描述
主动升沉补偿系统主要由母船、海洋绞车、三相异步电机、钢丝绳、水下装备、深度传感器等组成,其结构示意如图1所示。海洋绞车主动升沉补偿系统根据反馈控制原理,经由深度传感器、船舶姿态仪等其他传感器实时检测海洋绞车的工作参数传入控制器,经控制器处理后得到控制信号,控制信号进入变频器后,通过变频器控制电机转速与转向来驱动绞车滚筒,从而控制海洋绞车收放钢丝绳,实现主动升沉补偿功能。
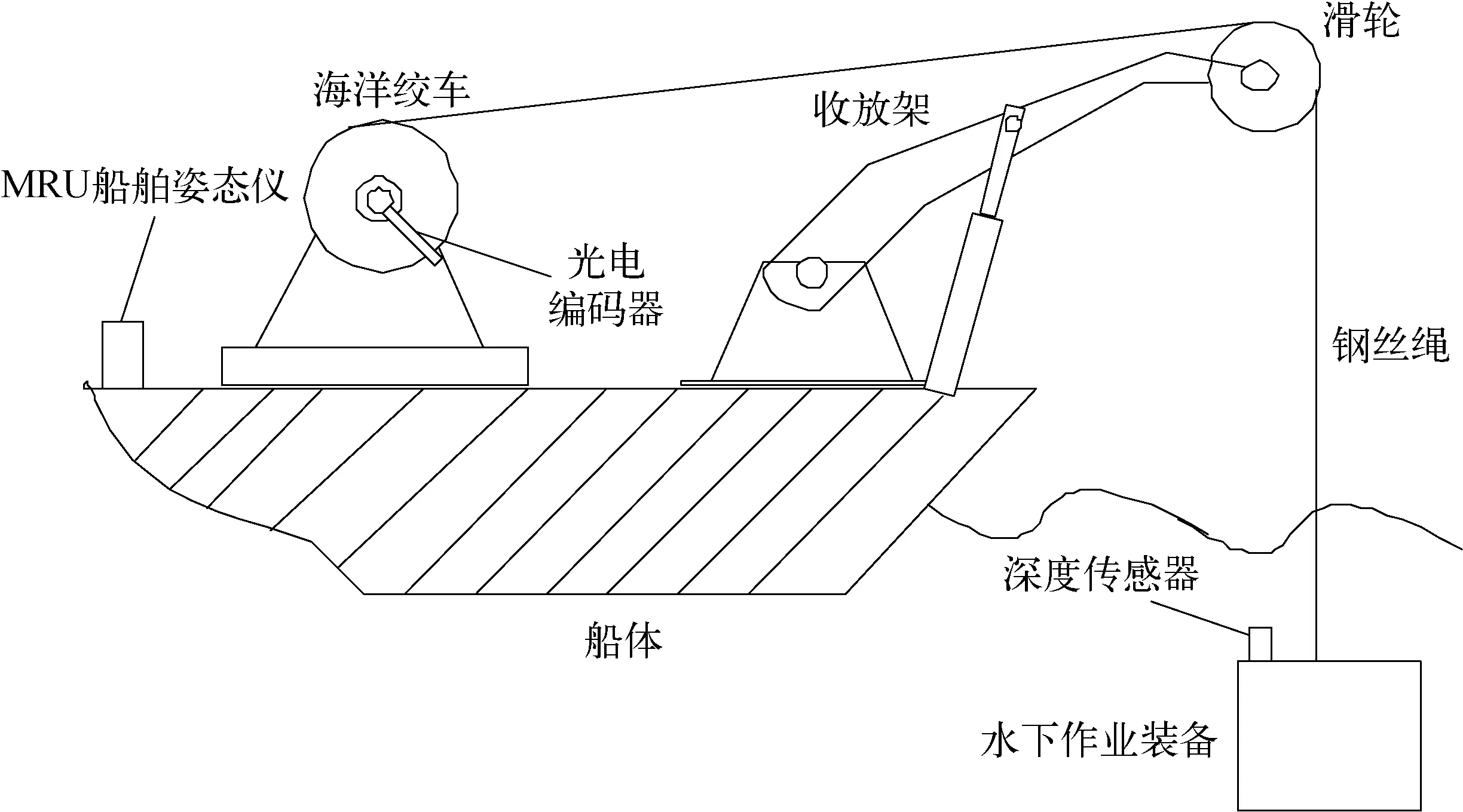
图1 主动升沉补偿系统结构示意
1.2 母船升沉运动数学模型
(1)
式中:y0为母船升沉位移,μ为升沉位移与有效波高比(一般取0.5),Hs为有效波高,Tw为波浪周期。
1.3 钢丝绳与负载耦合运动数学模型
由文献[11]可知,可将负载、钢丝绳、海水看作一个质量-弹簧-阻尼系统,系统运动方程:
(2)
式中:m为等效负载质量;C为海水阻尼系数;K为钢丝绳弹性刚度系数;y(t)为水下负载运动位移;y0(t)为母船升沉运动位移;r为滚筒半径;θ为滚筒转角;G0为升沉补偿静载荷。
由式(2)可求得负载运动位移对母船运动位移的传递函数:
(3)
负载位移对滚筒转角的传递函数为
(4)
等效负载质量m计算公式为
m=m1+m2+m3+m4
(5)
式中:m1为负载质量;m2为下放缆绳质量;m3为吊钩质量;m4为其它附加质量。
海水阻尼系数C为[12]
C=0.5ρ1A1Cd
(6)
式中:ρ1为海水密度;A1为负载有效截面积;Cd为阻尼系数。
钢丝绳弹性刚度系数K:
(7)
式中:E为钢丝绳弹性模量;A为钢丝绳横截面积;l为下放钢丝绳长度。

图2 三相异步电机运行状态示意
1.4 电机拖动绞车数学模型
异步电机拖动负载时,若其三相电流大小、频率与相序发生改变,三相异步电动机将会运行在不同状态,其运行状态曲线图如图2所示。当电机拖动负载正向运行时,此时电机转矩为正,电机转速也为正,负载转矩为负,电机处于电动运行状态,电机通过克服负载转矩对拖动系统作正功,工作点a即为正向电动运行点;而在第三象限时,即下放负载过程中,电机转矩为负,电机转速也为负,负载转矩为正,此时电机转矩为制动转矩,工作点b为反向电动运行点;同样地,在第四象限时,电机转矩为正,电机转速为负,工作点c为反向回馈运行点,拖动系统在整个过程中呈现出由动态趋向稳态、由稳态趋向动态的变化特点。
绞车拖动部分配备6台交流变频电机,电机与绞车滚筒采取小齿轮与内齿圈啮合方式连接,考虑电机轴扭转黏性阻尼c及电机轴等效扭转刚度k,则提升负载阶段,即三相异步电机处于第一象限时的绞车多轴拖动运动方程可表示为
(8)
同样地,下放负载阶段中的电机处于第三象限时的绞车多轴拖动运动方程为
(9)
而电机处于第四象限时的绞车多轴拖动运动方程可写为
(10)
式中:Te为单台电机输出转矩;TL为负载折算到电机轴转矩;GD2为转动部分等效飞轮矩;n为电机转速。
负载等效转矩TL为
(11)
将式(11)分别代入式(8)、式(9)、式(10)后得到提升负载与下放负载时各个阶段的绞车多轴拖动计算模型:
(12)
由此可分别得提升阶段与下放阶段各个阶段的滚筒转角对电机转矩的传递函数:
(13)
1.5 三相异步电机矢量控制系统模型
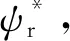

图3 三相异步电机矢量控制系统结构框图
(14)
(15)
式中:Tr为转子电磁时间常数;Lm为定子与转子同轴等效绕组间的互感;Lr为转子等效两相绕组的自感;ρ为极对数。
2r/2s变换模块计算公式:
(16)
与矢量变换角度θ1计算相关公式可表示:
(17)
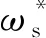
3s/2r变换模块由3s/2s模块与2s/2r模块组成,3s/2s模块计算公式:
(18)
2s/2r模块计算公式:
(19)
由式(18)、(19)可得3s/2r变换模块计算公式:
(20)
式中:isa,isb和isc为电机三相电流;isα,isβ为静止坐标中电流换算值。
SVPWM调制[13-14]原理:三相桥式逆变电路每个桥臂有两个开关管,其开关信号互补。三相桥式逆变电路各桥臂通断状态的组合为6个有效的空间矢量V4(100)、V6(110)、V2(010)、V3(011)、V1(001)、V5(101)和2个零矢量V0(000)、V7(111)。为了得到旋转空间矢量V,在不降低直流电压利用率情况下能调控三相逆变器输出的基波电压和消除低次谐波,可用矢量V所在扇区边界的两个相邻特定矢量Vx和Vy及零矢量Vz合成一个等效的电压矢量V,调控V的大小和相位。则在时间很短的一个开关周期Ts中,矢量存在时间就由组成这个区域的两个相邻的非零矢量Vx存在Tx时间、Vy存在Ty时间和零矢量Vz存在T0时间来等效,即:
VxTx+VyTy+VzT0=V(Tx+Ty+Tz)
(21)
2 仿真分析
基于以上模型、传递函数,在Simulink软件中搭建如图4所示的海洋绞车主动升沉补偿系统仿真模型[15-17],用于仿真负载在不同海况下海洋绞车主动升沉补偿系统的补偿能力。负载所在海水中的深度即钢丝绳下放长度,不同的钢丝绳下放长度对应不同的海洋绞车主动升沉补偿系统响应。负载质量为5 000 kg,当钢丝绳下放长度为1 400 m时,其等效负载质量m、等效转动惯量J、缆绳刚度系数K如表1所示。由分析可知:钢丝绳下放长度将改变负载位移响应函数。以海洋绞车在4级海况下的主动升沉补偿性能为研究目标,4级海况主要参数:有效波高1.25 m、2.5 m;波浪周期5 s、7 s。由式(1)分析可知:波浪的有效波高,波浪周期会改变母船升沉位移响应函数从而改变负载位移响应函数。
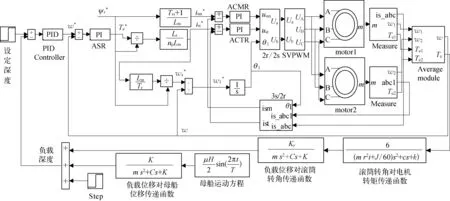
图4 海洋绞车主动升沉补偿系统仿真模型
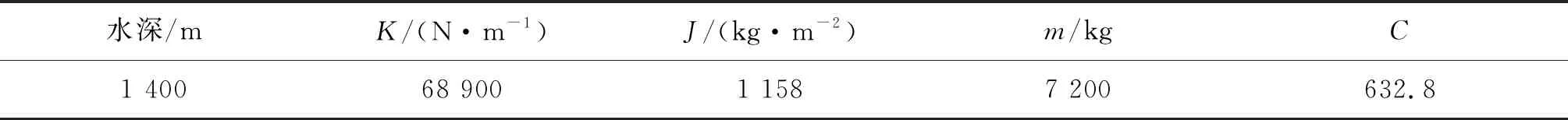
表1 深度为1 400 m时各参数
为了检验所设计的海洋绞车主动升沉补偿系统的升沉补偿性能,拟定仿真方案为:在钢丝绳下放长度为1 400 m时,分别在波浪周期为5 s、7 s进行有效波高为1.5 m、2.0 m、2.5 m下的系统仿真。
将仿真参数代入海洋绞车升沉补偿系统仿真模型中,得仿真结果如图5~10所示。由图5和图6可见,无补偿时负载位移(yu)在+1.12 m~-0.98 m、+0.85 m~-0.87 m内,有补偿时负载位移(yc)因补偿而大幅降低,其位移曲线在0 m刻度线上下波动,且波动幅度较小;波浪周期为5 s时,有补偿时负载位移与无补偿时负载位移比值达95%以上;波浪周期为7 s时,此值仍可达95%以上,即波浪周期对系统主动升沉补偿功能影响不大。对比负载位移与电机转速可见,电机输出反向转速来补偿负载位移,并由图7和图8可见,电机转速在-680~+510 r/min、-550~+100 r/min内变化。而波浪周期一定、有效波高越大时,电机补偿转矩越大。同样,在有效波高一定、波浪周期越小时,电机补偿转矩越大,转矩仿真图如图9和图10所示。
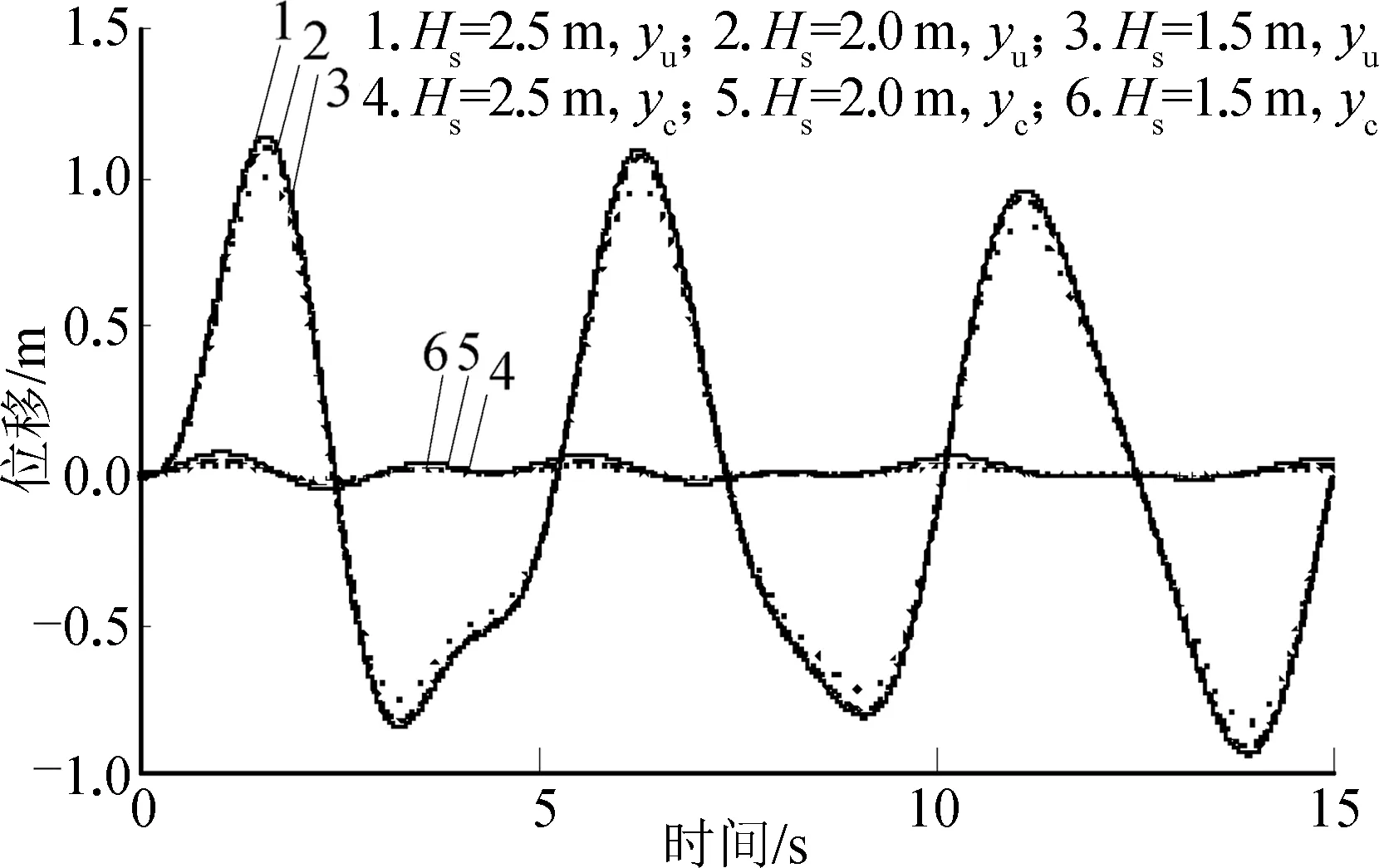
图5 T=5 s有无补偿时负载位移曲线
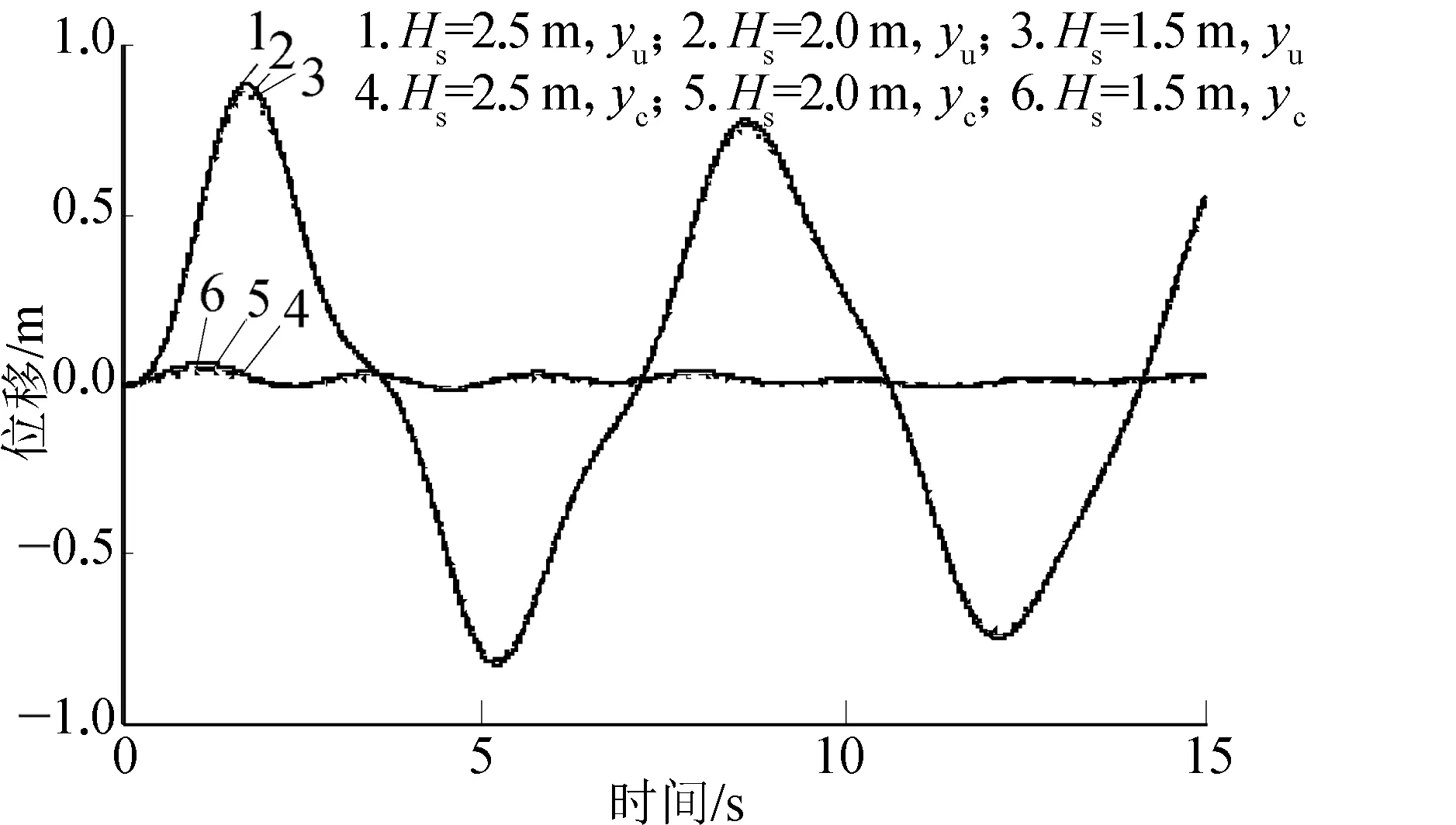
图6 T=7 s有无补偿时负载位移曲线

图7 T=5 s电机补偿转速
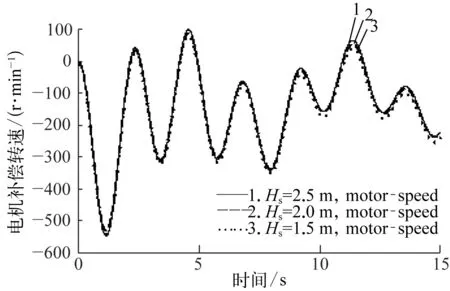
图8 T=7 s电机补偿转速

图9 T=5 s电机补偿转矩
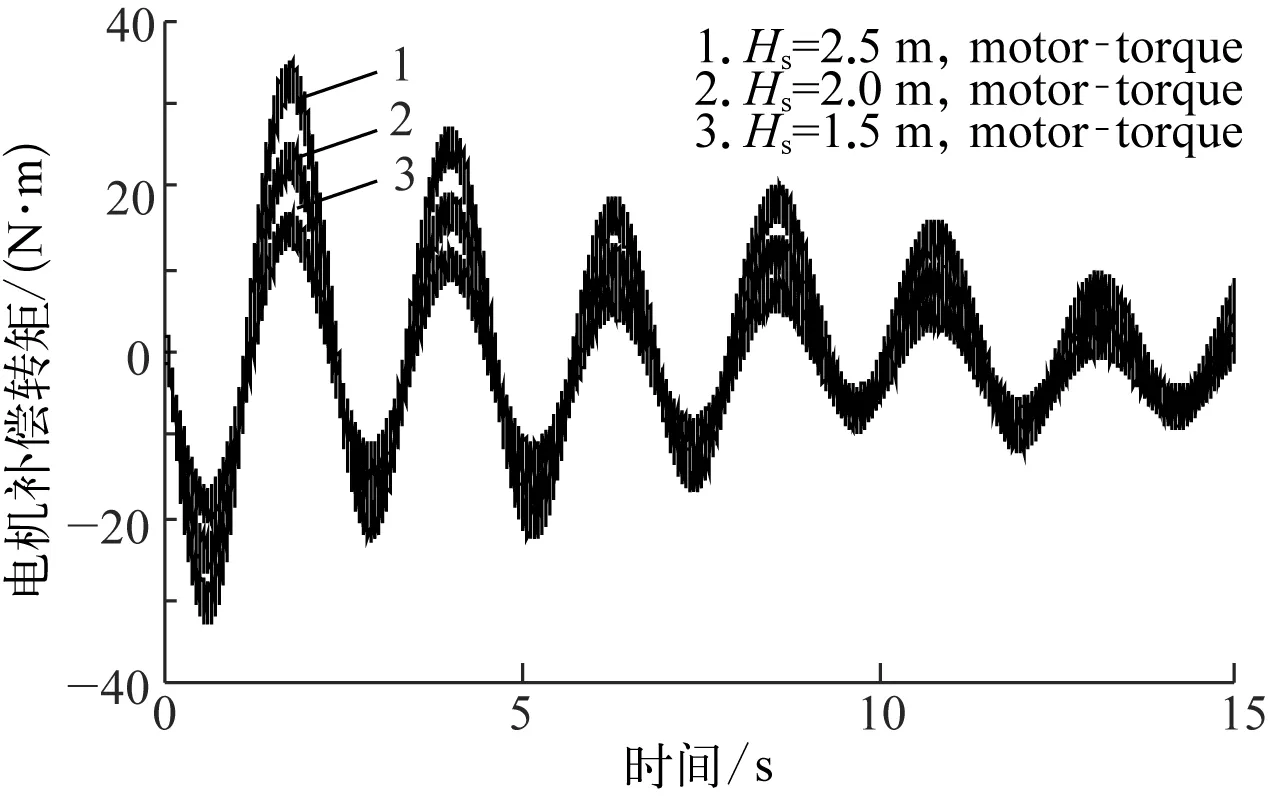
图10 T=7 s电机补偿转矩
3 试验研究
在PLC内部模拟四级海况的条件下,将主动升沉补偿系统通过PLC编程应用于电驱动海洋绞车上做升沉补偿试验。如图11所示,实验平台由海洋绞车、实验塔架、钢丝绳、负载等组成,实验塔架高42 m,负载通过定滑轮系与海洋绞车相连接。海洋绞车滚筒末端上安装有1个编码器,用于海洋绞车进行升沉补偿试验时测量滚筒转速,通过编写程序可将获取的转速换算成负载的实时位移显示于上位机监控界面。

图11 试验平台
为切实研究系统的升沉补偿性能,拟定试验方法如下:海洋绞车固定不动,通过PLC模拟四级海况(海浪周期分别为5 s、7 s),控制卷筒转向和转速,在负载质量5.0吨(安全工作载荷的35%)时进行升沉补偿试验。单组试验重复3次。在IFIX软件中编写脚本生成历史报表,采集主动升沉补偿试验数据并取其中一组数据绘制其随时间变化的曲线图,如负载补偿位移及电机补偿转矩。取负载补偿位移值与补偿位移预期值作对比,得到两者的位移-时间曲线图如图12和图13所示,负载补偿位移试验数据如表2所示。取不同模拟海况下的电机补偿转矩中心值,绘制电机转矩随时间变化曲线如图14和图15所示。
由图12、图13及表2数据可见,四级模拟海况下的系统主动升沉补偿值与预期值随时间的变化曲线符合预期的曲线变化规律,且平均补偿率达到了95%,系统主动升沉补偿效果理想,有利于将海浪运动与负载运动进行相互解耦。因海洋绞车升沉补偿系统中的通信及控制等因素的影响,系统主动升沉补偿功能存在一定的时滞性。同时,因系统数据采集平台受电磁干扰影响,电机转矩数据受谐波干扰,故取电机转矩中心值对其绘图。结合电机转矩仿真图及试验采集所得数据绘制所得转矩试验图14与图15可见,试验所得转矩较仿真所得转矩在幅值上偏大,但其转矩变化规律基本与仿真转矩变化规律吻合,充分证明系统建模的合理性。
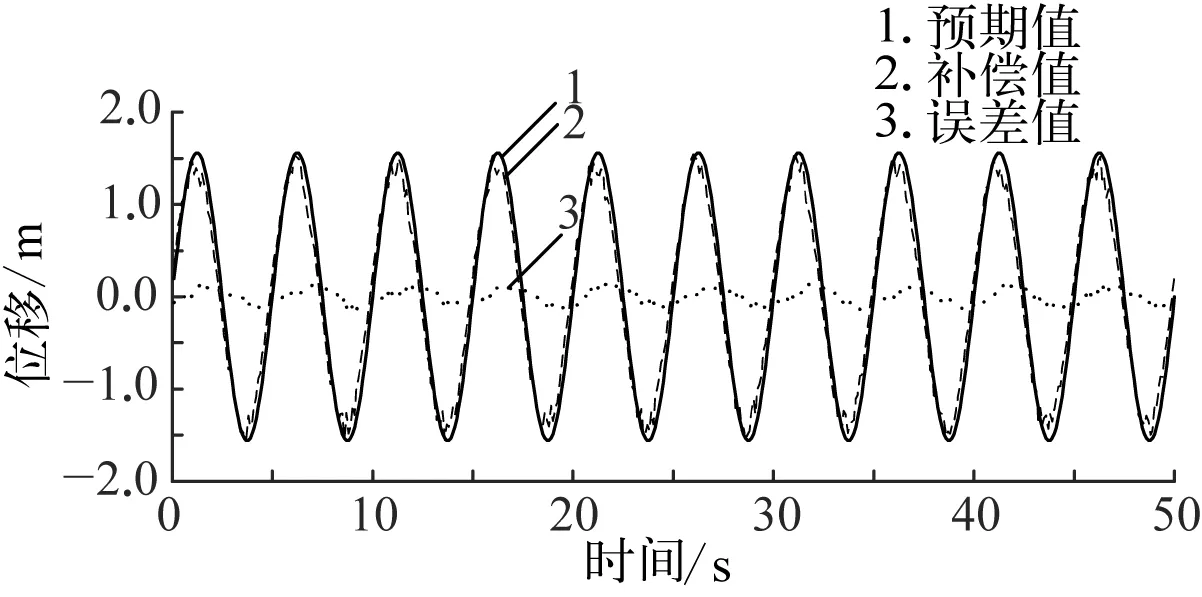
图12 波浪周期为5 s时的主动升沉补偿位移试验结果
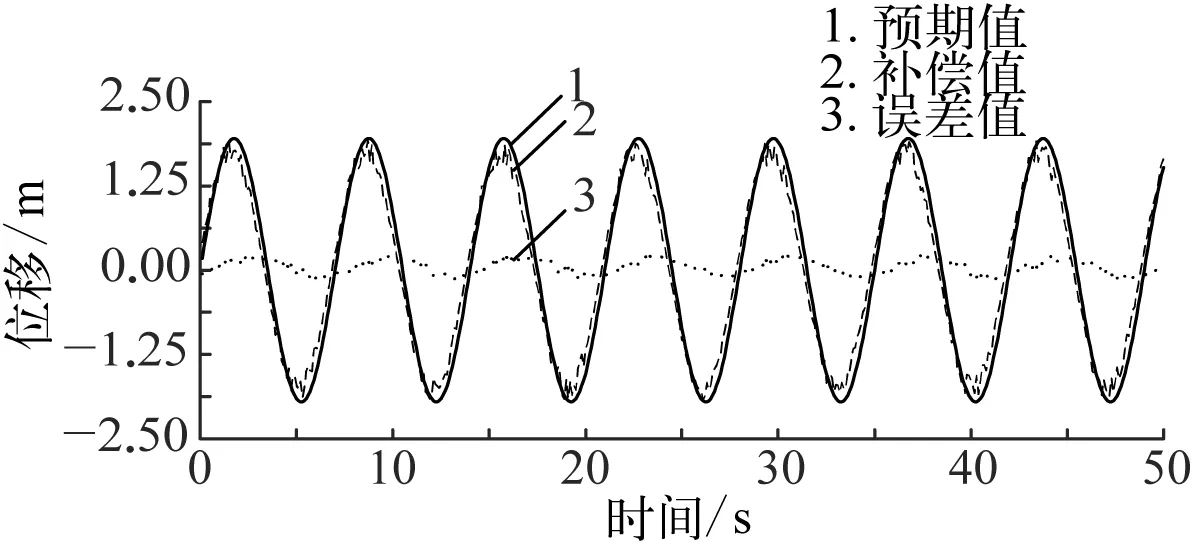
图13 波浪周期为7 s时的主动升沉补偿位移试验结果

表2 四级模拟海况下试验结果

图14 波浪周期为5 s时的主动升沉补偿转矩试验结果
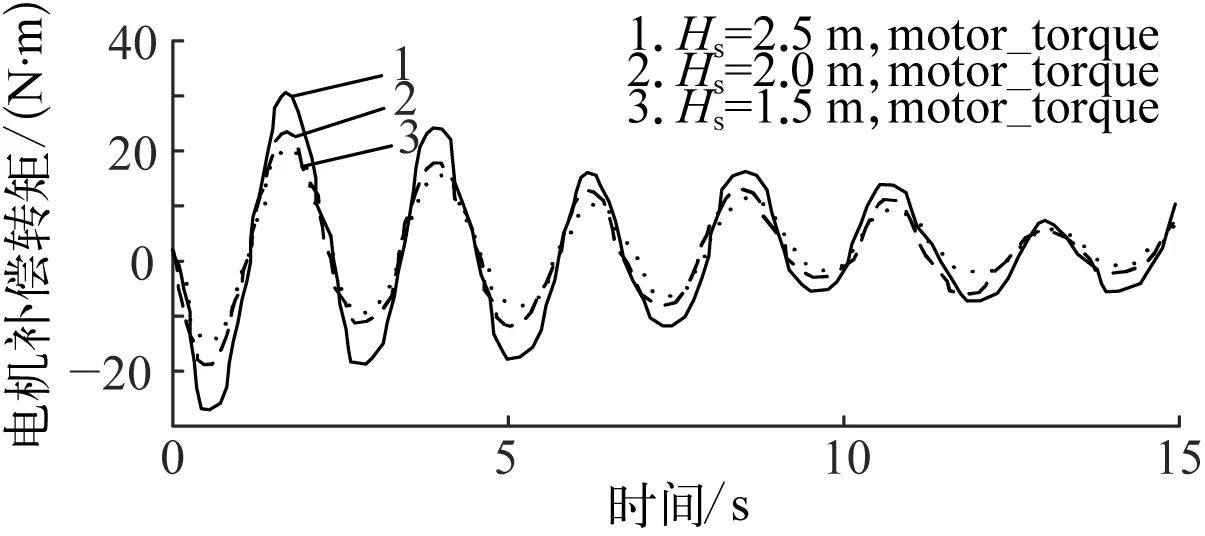
图15 波浪周期为7 s时的主动升沉补偿转矩试验结果
4 结 语
1) 通过对主动升沉补偿系统的控制机理进行分析,在Simulink软件中构建了海洋绞车主动升沉补偿系统仿真模型。
2) 在不同水深和海况对此主动升沉补偿系统进行仿真研究发现:有效波高对母船与负载的位移影响较大,海浪周期对电机补偿时转速及转矩影响较大;主动升沉补偿系统的补偿性能满足设计要求,为后续的开发提供了理论依据。
3) 从试验结果可以看出,四级海况下的带载主动升沉补偿试验,其补偿率达到了95%且试验所得转矩变化规律与仿真所得转矩变化规律吻合,系统建模合理且整体补偿能力满足设计要求,可为海洋绞车主动升沉补偿系统性能改进与完善提供参考。

