基于时域分析法的黏滞阻尼器消能减震结构设计与分析

孙宁乐 关 群

（合肥工业大学土木与水利工程学院，合肥230009）

0 引 言

实际地震作用是水平和竖直的多维振动，其对建筑物的破坏较单向水平振动对建筑物的破坏更为严重［1］。《建筑抗震设计规范》［2］中，对框架结构的抗震验算主要沿主轴方向，但是由于实际设计要求和随机因素的影响，实际结构各层的质量中心与刚度中心不重合，实际地震作用的方向与主轴也不重合。因此在双向水平地震下，结构的振动表现为平移和扭转的形式，加速结构抗震性能退化和破坏［3］。消能减震结构是给结构层间、节点等位置设置了消能器的结构，黏滞阻尼器为结构提供附加阻尼，在地震发生时就能发挥减震作用，减小发生共振时的振幅峰值，对结构构件的二次损伤小，被广泛运用在消能减震结构上。但是由于建筑结构布局和功能的要求，阻尼器难以均匀布置［4］，规范［2］给出在不同阻尼比下的反应谱曲线，并考虑等效附加阻尼比的反应谱，进而计算结构的地震响应［5］。因此，附加阻尼参数的确定是消能减震结构设计的关键。

在阻尼器选择方面，国巍等［7］对比了三类阻尼器对结构抗倒塌性能的控制效果，认为速度型黏滞阻尼器控制效果最优，位移型摩擦阻尼器和防屈曲支撑次之。基于时程分析，丁永君等［6］使用层间模型，推荐了能量比法和平均减震系数法。从能量的角度作为减震效果量化的指标，其精度很高但是计算不便。从工程实际的角度出发，结构的质量中心和刚度中心不重合，实际结构的节点破坏特征比较复杂，以简化的串联钢片模型进行结构动力分析，用位移、速度等易于测量和计算的指标进行减震设计更为准确、方便。

本文将黏滞阻尼器消能减震结构简化为串联钢片体系，在线弹性阶段将简化的地震分析模型视为控制系统，结合状态空间法，根据传递函数模型和状态空间控制模型相互转化的原理，对黏滞阻尼器消能减震结构进行时域分析，确定附加阻尼的最优参数，对其进行减震设计。

1 结构控制系统的建立

在双向水平地震下，结构的振动一般表现为两个方向的水平位移和一个水平转动位移。本文将实际结构简化为串联钢片体系。附加阻尼器结构振动分析计算模型如图1所示，各层质量为mi，转动惯量Ji，以各层质心为坐标原点，各层水平位移分别为xi、yi，各层转角为θi。第i层质心坐标为xci、yci。第i 层 刚 心坐标为xmi、ymi。第i 层 质心与刚心沿x、y 方向的距离分别为exi、eyi，第i 层与第i+1 层之间的质量中心距离分别为。ai、bi为第i层楼板的等效长宽。黏滞阻尼器的计算模型采用线性模型，其表达式为

式中：fa为附加阻尼力；ca为阻尼系数；ẋ为阻尼器运动的速度。

根据结构动力学原理，附加阻尼器结构的运动微分方程为

对于质心和刚心不重合的结构，其中，

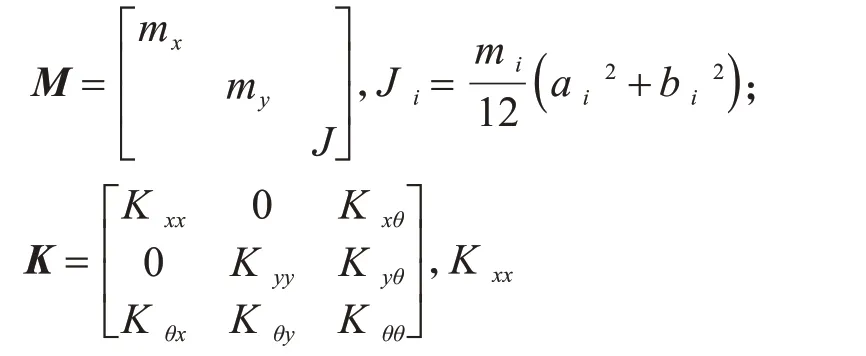
式中：Kxx、Kyy分别表示结构在x、y方向上的平动刚度，Kxθ、Kyθ分别表示结构在x、y 方向的平扭刚度；Kθθ为结构的扭转刚度矩阵。

本文将黏滞阻尼器消能减震结构视为一个控制系统。如图2 所示，将地震波视为干扰信号输入，各层产生位移、速度和加速度为输出响应，阻尼器提供的附加阻尼对输入信号响应的影响，可视为对系统的反馈控制，所以由结构和附加阻尼器组成的结构控制系统是一个闭环控制系统。

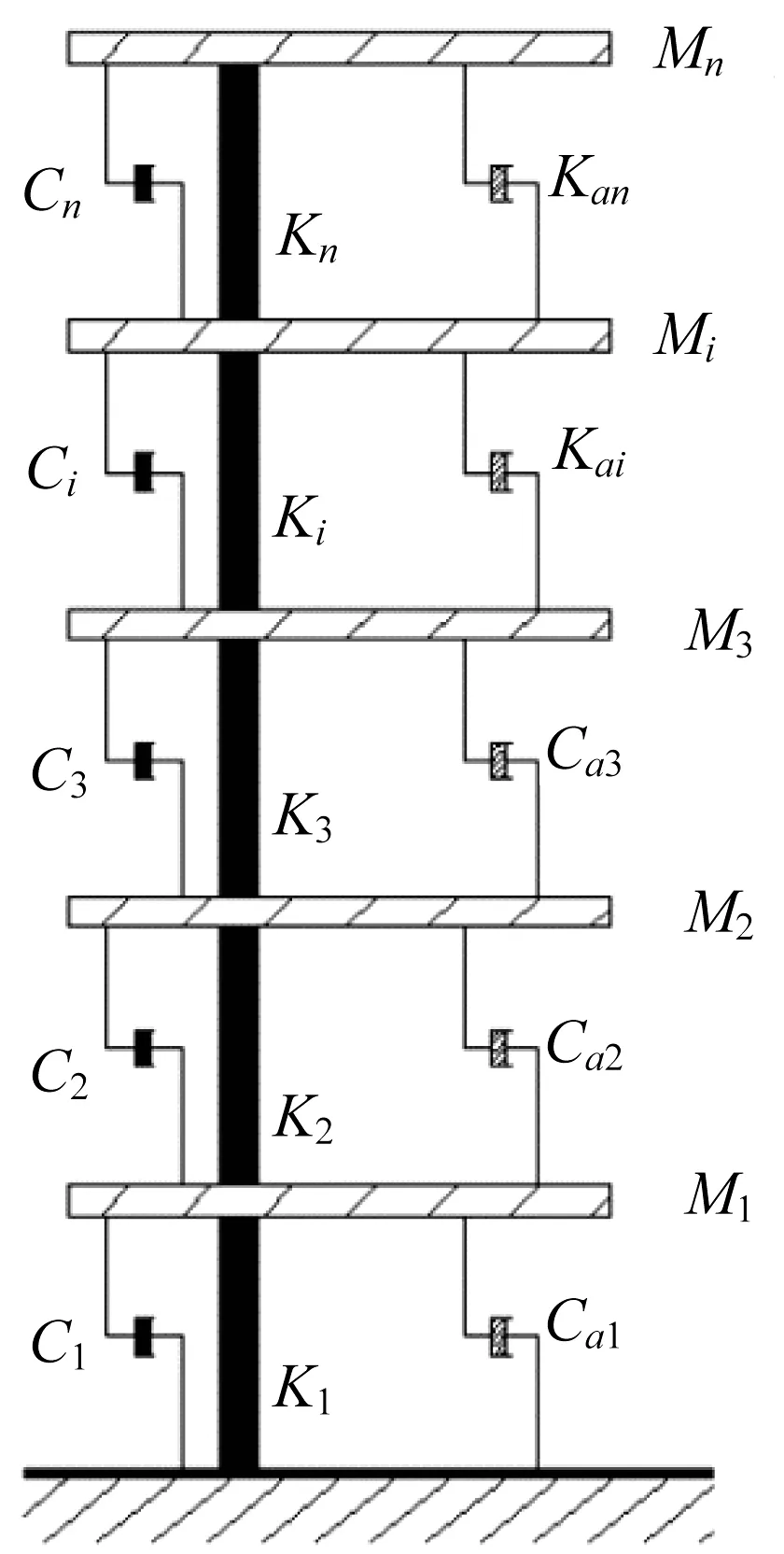
图1 计算模型Fig.1 Calculation model

图2 结构控制系统Fig.2 Control system of the structure

结构运动微分方程一般采用Wilson-θ 法、Newmark-β 法、中心差分法、振型叠加法等方法进行求解，求解过程中通常需要解决高阶线性方程组数值解不收敛于精确解的问题。运用状态空间理论，可以将结构运动微分方程转化为时域一阶微分方程组，该方法具有无条件稳定和精度高的特点。状态空间模型是以时域分析为主的数学模型，反映了控制系统内部状态和内部联系，揭示了系统内部状态和外部输入和输出变量的联系，对于多输入与输出，状态空间模型具有表达直观的优势［8］。对于线性系统，传递函数模型以拉普拉斯变换为基础，在基于参数对系统进行调节等方面具有明显优势［9］。传递函数和状态空间是一个问题的两种表达形式，因此可以运用传递函数模型的参数控制思想对状态空间模型构成的控制系统进行控制和调节。结构输出响应包含位移、速度和加速度等多个参数，所以结构控制系统中M、C、K 模块应采用具有多输入、多输出特性的状态空间模型进行建模，M、C、K 模块亦可视为反映原结构特性的前向传递函数。其状态空间模型的数学表达式为

式中：x、y、u 分别表示状态向量、输出向量和输入向量；A、B、C、D 分别表示状态矩阵、控制矩阵、输出矩阵和联系矩阵。

E、0分别表示n×n维单位矩阵和零矩阵。当原结构构件产生相对位移时，黏滞阻尼器提供一定的附加阻尼Ca，Ca模块在结构控制系统可视为反馈传递函数，起到控制状态的作用。因此状态矩阵A在考虑Ca模块应为

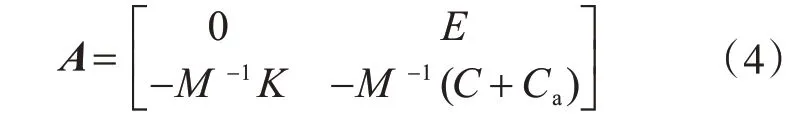
矩阵分离后得到Ca模块的控制矩阵，即M、C、K模块的反馈矩阵为

2 控制系统的时域分析

运用状态空间法所建立的结构控制系统，是基于结构动力分析模型的运动微分方程转化为状态方程所建立的。以振型叠加法为基础，振型为坐标基，就可以得到一组非耦连的多自由度体系运动方程，模态坐标X(t)是一种广义的唯一坐标，与自然坐标x(t)之间的关系为

在时间域内研究控制系统在一定输入信号的作用下，其输出信号随时间的变化称为系统的时域分析。控制系统的时域分析以拉普拉斯变换为工具，从传递函数出发，建立在系统输入信号的基础上，在输入信号的作用下得到系统的各项性能指标。单位阶跃信号在物理上比较容易实现，可以使系统既能有明显的瞬态反应和稳态反应，同时相对于其他多数信号，阶跃信号对结构往往是最不利情况。本文建立的控制系统实际输入信号是地震波，具有突变性质，因此本文在系统试验阶段选用单位阶跃信号来评价系统的瞬态和稳态特性，测定系统的性能指标典型的单位阶跃响应信号如图3所示。

欠阻尼（0<ξ<1）系统属于标准二阶系统，其单位阶跃响应表达式为

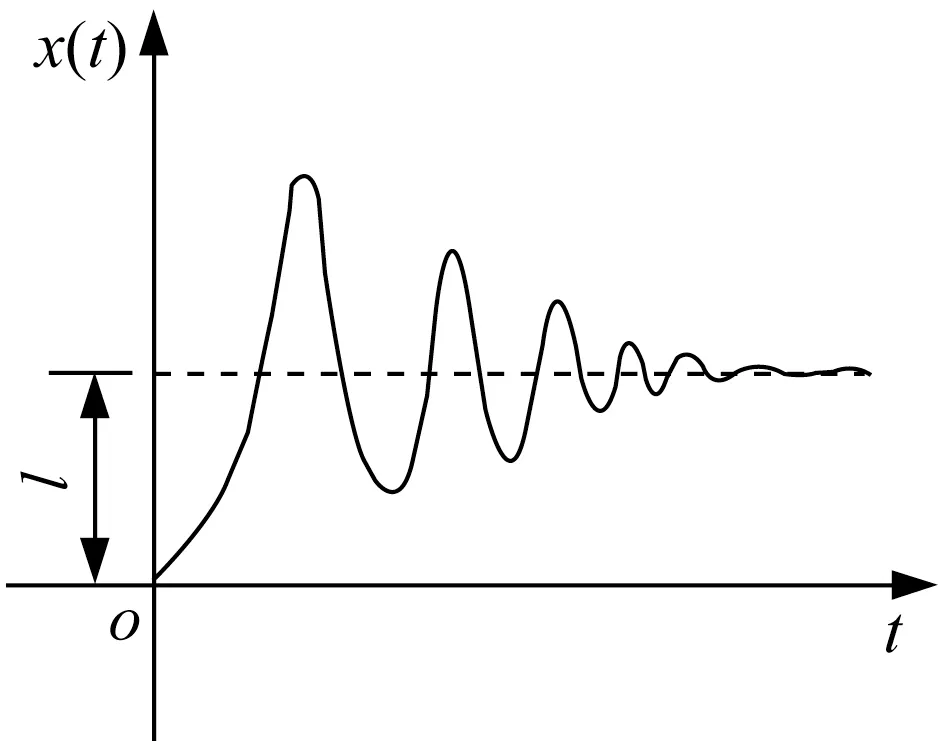
图3 典型单位阶跃响应Fig.3 Typical unit step response

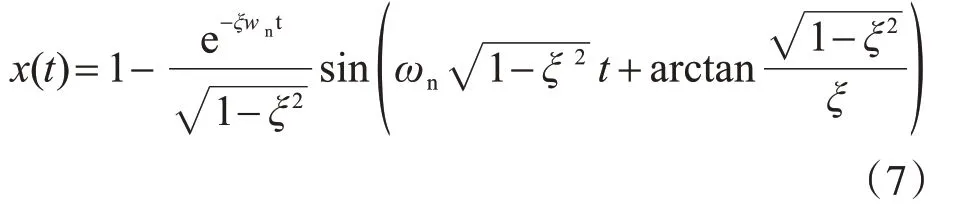
ωn为固有频率。通过采集二阶系统单位阶跃响应曲线图上相隔p 个周期的波峰值，利用式（8）由阶跃响应曲线对数衰减率计算各层阻尼比ξxi、ξyi。

3 结构减震设计

由动力学原理可知，在原结构抗侧刚度一定的情况下，附加阻尼不仅可以使结构在地震作用的瞬间吸收地震能量，降低结构的固有频率，减小发生共振时的振幅大小，同时对于某些存在疲劳破坏风险的结构来说，附加阻尼会起到增加疲劳寿命的作用。附加阻尼过多会使结构产生动刚度同时也会造成经济浪费。本控制系统对外界激励的响应要达到及时、稳定的效果，需要使附加阻尼后的每个楼层都达到临界阻尼状态。

根据自然坐标和模态坐标之间的关系，将每个楼层的单位阶跃响应视为独立的二阶欠阻尼系统的响应，根据每条响应曲线图中相隔p 个周期的振动峰值，计算出每层楼被视为独立二阶系统响应分析时的阻尼比。附加阻尼后的每个楼层基于单位阶跃响应分析时的附加阻尼比的计算式为

根据阻尼比和阻尼系数的关系可以得到：

Ca(xx)、Ca(yy)，分别表示结构在x、y 方向上附加阻尼。Ca(xθ)、Ca(yθ)分别表示结构在x、y 方向上的平扭附加阻尼。

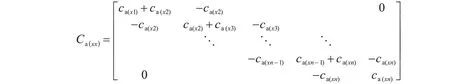
从线性变换的角度，实际结构附加阻尼矩阵Ca和基于独立二阶系统响应分析时所需附加的阻尼矩阵Ca若要产生一致的效果，则矩阵Ca要相似于对角阵C'a，由此关系可解出矩阵Ca中的每个附加阻尼系数ca(i)，进而确定各层结构所需附加阻尼系数值。

根据以上方法确定的黏滞阻尼器参数对结构进行动力分析，检验是否可以达到对输入或产生的扰动能快速稳定的结构减震设计目标。

4 计算实例

4.1 基本参数

某6 层钢筋混凝土建筑物，层高均为3.3 m，抗震设防为八度。xm、ym分别表示结构的质量中心坐标。第1 至5 层的集中质量为7.10×105kg，x向侧向刚度为50×107N∕m，y 向侧向刚度为45×107N∕m，质量中心坐标为（5.1，5.1），转动惯量为1.1×108kg·m2。第6层集中质量为6.0×104kg，质量中心坐标（7.55，7.45），转动惯量为1.0×106kg·m2，x向侧向刚度为11×107N∕m，y 向侧向刚度为10×107N∕m。原结构的一阶阻尼比为ξ1=0.05。采用本文的减震设计方法，为该结构选定设置在每一层的黏滞阻尼器的附加阻尼值。输入地震波为双向Elcentro波，峰值加速度为0.2 g。

4.2 附加阻尼系数计算

首先，由工况数据计算结构的质量矩阵、刚度矩阵和阻尼矩阵，并建立结构控制系统。然后向该控制系统输入x方向和y方向的单位阶跃信号，计算得到各楼层的和阻尼比ξxi、ξyi和附加阻尼比，并由式（10）计算得到各楼层所需附加的阻尼系数，如表1、表2所示。

表1 x方向各层 参数计算表Table 1 Calculation table for parameterof each layer in the x direction

表1 x方向各层 参数计算表Table 1 Calculation table for parameterof each layer in the x direction

表2 y方向各层参数计算表Table 2 Calculation table for parameterof each layer in the y direction

表2 y方向各层参数计算表Table 2 Calculation table for parameterof each layer in the y direction

由表1-2 的计算结果以及矩阵Ca和对角阵相似关系，得到各楼层x、y 方向附加阻尼系数cax(i)、cay(i)，如表3所示。

表3 x、y方向各层所需附加的阻尼系数表Table 3 Table for added damping of each layer in need

4.3 结构减震设计分析和结果

图4 和图5 分别表示算例在未附加阻尼和附加阻尼后的两种情况下，在输入单位阶跃信号后各层结构x 向的相对位移随时间变化的趋势。图6 和图7 分别表示算例在未附加阻尼和附加阻尼后的两种情况下，在输入单位阶跃信号后各层结构y 向的相对位移随时间变化的趋势。从曲线图中可以看出，在附加阻尼后，不仅消除了结构的自振响应，而且由结构自振引起的振动响应部分在附加阻尼后迅速达到临界稳定状态。

图8 为算例结构第6 层在未附加阻尼和附加阻尼的情况下输入双向地震波后的位移响应曲线。从响应曲线中可以看到结构顶层的位移大幅度减少，两种情况下x 方向上的最大位移分别为13.41 mm、4.12 mm，y 方向上的最大位移分别为14.97 mm、1.34 mm。

图4 原系统x向的单位阶跃响应曲线图Fig.4 Unit step response curves of the original system of the structure in the x direction

图5 附加阻尼后的x向单位阶跃响应信号曲线图Fig.5 Unit step response curves of the condition of adding damping later in the x direction

图6 原系统y向的单位阶跃响应信号曲线图Fig.6 Unit step response curves of the original system of the structure in the y direction

图9 和图10分别为算例结构顶层在未附加阻尼和附加阻尼情况下，输入双向地震波后结构各层的转动位移与时间的关系曲线图。以顶层为例，在8 度罕遇地震作用下，原系统结构的最大转动位移为1.423×10-5rad，附加阻尼后的系统结构的最大转动位移为9.873×10-7rad，附加阻尼后的结构转动位移的峰值大幅减小。同时对比两张曲线图可以得出，附加阻尼后结构的振动频繁程度大大降低。通过本文的设计方法得到的阻尼参数，可以使结构的转动位移迅速减小，充分发挥阻尼体系的抗震作用。

图7 附加阻尼后的y单位阶跃响应信号曲线图Fig.7 Unit step response curves of the condition of adding damping later in the y direction

图8 结构顶层位移-时间图Fig.8 Displacement x∕y-time t of top layer of structure

图9 原系统结构转动位移时程曲线图Fig.9 The rotational displacement time history curves of the original system

5 结 论

图10 附加阻尼后系统结构转动位移时程曲线图Fig.10 Time-history curves of rotational displacement of system structure after additional damping

本文针对实际结构刚度中心和质量中心不重合的情况，把结构简化为串联钢片体系，在多维地震下，将简化的地震分析模型视为控制系统，对其进行减震设计，确定附加阻尼参数的最优设置。得出结论如下：

（1）将结构转化为控制系统，利用状态空间法进行时域分析。在构建结构的总体刚度矩阵时，不仅需要考虑两个水平方向的平动刚度，而且还要考虑平扭刚度，才能够对应得到附加阻尼矩阵的平动附加阻尼和扭转附加阻尼。

（2）运用模态坐标与物理坐标的线性变换关系，基于物理坐标采用时域分析法设计的结构临界阻尼体系可以让各层动力响应迅速达到临界阻尼状态。

（3）运用本文的方法，计算得到的附加阻尼值可以准确快速地使各层结构达到临界阻尼状态，而且可以抑制结构自振产生的扰动，最大限度地优化结构的阻尼体系，对质量中心和刚度中心不重合结构的减震设计具有借鉴意义。