往复荷载作用下部分填充混凝土箱形截面钢桥墩的破坏模式
刘富平 高圣彬
(1.上海交通大学船舶海洋与建筑工程学院土木工程系,上海200240;2.上海师范大学建筑工程学院,上海201418)
0 引 言
部分填充混凝土钢桥墩由于其质量轻、强度高、延性好的特点逐渐得到广泛应用。在1995 年的兵库县南部地震中,观察到钢桥墩的两种不同破坏模式,一种为钢桥墩由于局部屈曲导致承载力大幅降低而破坏,另一种为钢桥墩产生延性裂纹,之后裂纹扩展,最后发生延性断裂[1-2]。进一步的研究表明,这种延性裂纹的萌生是由一种全新的破坏模式引起的,被称为超低周疲劳破坏[3]。超低周疲劳破坏是指延性金属在极大的塑性应变幅作用下,在循环几十次甚至几次后便发生断裂,这种形式的疲劳破坏不同于传统的高周疲劳破坏[4]。超低周疲劳破坏的典型破坏模式为延性断裂,其破坏由塑性损伤控制,包括空隙成核、空隙聚集和裂纹萌生扩展等阶段[5-6]。在部分填充混凝土钢桥墩的抗震设计中,有必要综合考虑屈曲破坏和超低周疲劳破坏的影响。部分填充混凝土钢桥墩因其本身构造复杂,影响其破坏模式的因素较多,试验存在工作量大、耗时长、费用昂贵等问题,因此使用数值模拟方法成为解决该问题的一个重要手段。
文献[7]提出了统一高周和低周的疲劳性能预测模型,并将其用于金属材料疲劳性能的预测,预测结果和试验结果吻合较好。文献[8]提出的模型考虑了裂纹开展和闭合对于刚度退化的影响,能够准确预测试件的损伤状态和疲劳寿命。Usami等学者[9]研究了翼缘正则化宽厚比、试件正则化长细比、轴压比和混凝土填充率等参数对部分填充混凝土钢桥墩延性性能的影响。文献[10]采用有效缺口应变法对部分填充混凝土钢桥墩角部的超低周疲劳裂纹萌生寿命进行了预测,其结果与试验结果吻合较好。
Ge 等[11]提出了基于塑性应变幅的损伤累积模型,以下简称为Ge 模型,Ge 模型可以实现对超低周疲劳裂纹萌生寿命在结构水平上的精确预测。文献[12]指出Ge 模型的局部损伤法在预测超低周疲劳裂纹萌生寿命时对网格密度大小比较敏感。针对这一缺陷,提出了非局部损伤法,并将非局部损伤法用于预测纯钢桥墩的超低周疲劳裂纹萌生寿命。研究结果表明,非局部损伤法对网格密度大小的敏感性大为降低,可用于精确预测纯钢桥墩的超低周疲劳裂纹萌生寿命。文献[13]指出,网格尺寸为2 mm×2 mm 的Ge 模型非局部损伤法适用于预测纯钢桥墩的超低周疲劳裂纹萌生寿命。由于国内外学者对部分填充混凝土钢桥墩破坏模式的研究较少,因此开展针对部分填充混凝土钢桥墩的破坏模式研究,可以为该类钢桥墩的抗震设计提供理论依据。
本文采用弹塑性有限元分析方法对部分填充混凝土钢桥墩在轴压比分别为0.1、0.2 和0.3 情况下的超低周疲劳裂纹萌生寿命和局部屈曲寿命进行研究。通过参数化分析,研究不同翼缘正则化宽厚比、试件正则化长细比和轴压比等参数对试件超低周疲劳裂纹萌生寿命和局部屈曲寿命的影响规律。基于参数化分析结果提出预测该类钢桥墩超低周疲劳裂纹萌生寿命和局部屈曲寿命的经验公式。通过对这两种破坏模式下的寿命进行比较,提出确定部分填充混凝土钢桥墩实际破坏模式的方法。
1 分析方法
1.1 有限元分析模型
使用ABAQUS 软件建立部分填充混凝土钢桥墩的三维弹塑性有限元分析模型。钢板采用四节点壳单元(S4R)。为了考虑壳单元在厚度方向的塑性发展,沿板厚方向设置了5 个积分点。混凝土采用八节点实体单元(C3D8)。考虑到钢桥墩在荷载和结构上的对称性,只需建立1∕2 模型。根据文献[14]的研究结果,与考虑焊缝的模型相比,不考虑焊缝的模型预测结果更偏于安全且误差不大,因此在建模过程中不考虑焊缝。根据文献[15]的研究结果,网格尺寸为2 mm×2 mm 的Ge 模型非局部损伤法比较适用于部分填充混凝土钢桥墩的超低周疲劳裂纹萌生寿命预测。通过对以往试验结果的观察发现[16-17],超低周疲劳裂纹萌生在钢桥墩底部翼缘和腹板连接处。因此,本文在应变集中部位划出10 mm×10 mm 的区域,采用2 mm×2 mm的网格尺寸来细分该区域。
钢板和混凝土的法向接触采用只受压不受拉的硬接触模型,切向接触采用摩擦系数为0.4的摩擦型模型[18]。此外,在试件底部建一块刚性板,模拟试验时混凝土底部的钢板,并假设该钢板与基础固结。部分填充混凝土箱形截面钢桥墩的立面、横截面以及有限元网格划分如图1 所示,其中,h为钢桥墩高度,lc为混凝土填充高度。
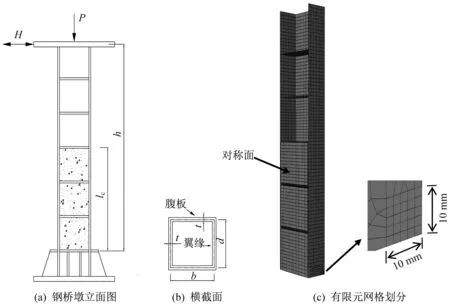
图1 钢桥墩分析模型Fig.1 Analytical model of steel bridge piers
1.2 材料属性
1.2.1 钢材材料属性
钢材的本构模型采用文献[19]中的Lemaitre-Chaboche 混合强化模型。该模型兼具等向强化和随动强化的特点,可以准确模拟钢构件在往复荷载作用下的滞回性能,钢材的材料特性如表1所示。表1 中,σ0为钢材屈服强度,Q∞和b 为各向同性模型参数,Q∞定义了屈服面最大变化值,b定义了屈服面随塑性应变增加而变化的比率;Ck和γk为随动强化模型参数,定义了背应力的最大变化值,γk定义了背应力随塑性应变增加而变化的比率[20]。
1.2.2 混凝土材料属性
混凝土采用由Lubliner 等[21]提出的损伤塑性模型。该模型考虑了混凝土在往复荷载作用下的受拉开裂和受压破碎,分别使用受拉损伤因子dt和受压损伤因子dc反映混凝土受拉损伤和受压损伤的程度,同时引入恢复系数表示混凝土在往复荷载作用下的刚度恢复。混凝土的抗压强度为28 MPa,弹性模量为29 075 MPa,均由材性试验测得。
1.3 加载制度
如图1(a)所示,先在柱顶施加恒定的竖向荷载P,然后使用位移控制方式施加水平往复荷载H。水平往复荷载包括C1、C3 和CC 三种加载形式[12],如图2所示。其中,C1指每级位移幅循环一次,每级位移幅加载结束后增加1 倍的水平屈服位移;C3 指每级位移幅循环三次,每级位移幅加载结束后增加1 倍的水平屈服位移;CC 指水平位移幅值恒定为5δy的往复加载。图2 中,δ 为水平位移,δy为水平屈服位移,其计算公式如下:
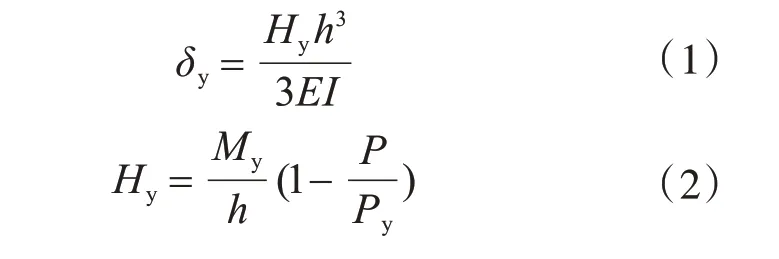
式中:Hy为钢桥墩的水平屈服荷载;E 为钢材弹性模量;I 为横截面惯性矩;My为钢桥墩横截面屈服弯矩;P 为所施加的恒定竖向荷载;Py为全截面屈服荷载。
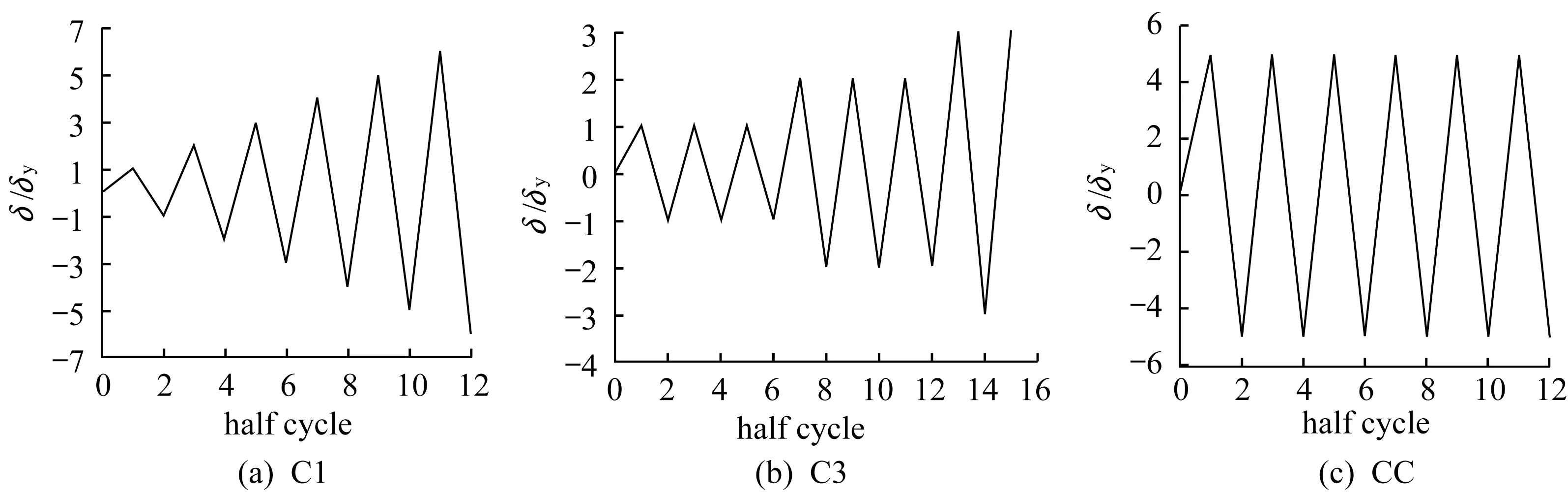
图2 水平往复荷载加载形式Fig.2 Lateral cyclic loading patterns

表1 钢材的材料特性Table 1 Material properties of steel
1.4 Ge模型中的非局部损伤法
Ge 模型根据选取的计算区域以及权重不同分为局部损伤法和非局部损伤法。Ge 模型非局部损伤法是指在塑性应变集中部位选定一块区域作为计算累积损伤D 值的范围,采用该区域内的带权重平均塑性应变来计算累积损伤值。当累积损伤D 值达到1 时,表示萌生了超低周疲劳裂纹,其计算公式如式(3)所示[11]。
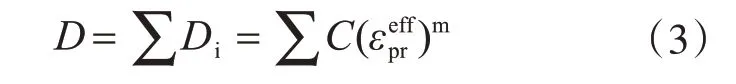
本文将钢桥墩脚部翼缘和腹板交接处的10 mm×10 mm 区域局部加密至2 mm×2 mm,采用Ge 模型非局部损伤法来预测部分填充混凝土钢桥墩的超低周疲劳裂纹萌生寿命。该模型的准确性已由笔者在文献[15]中得到验证。
2 钢桥墩裂纹萌生寿命和局部屈曲寿命的参数化分析
本节针对不同翼缘正则化宽厚比、试件正则化长细比和轴压比的试件进行参数化分析,研究上述参数对试件裂纹萌生寿命和局部屈曲寿命的影响规律。其中,局部屈曲寿命指试件承载力下降到最大承载力的95%时所对应的往复加载半周期数。
根据以往的试验[16],30%混凝土填充率的试件的破坏模式均为局部屈曲破坏,50%混凝土填充率的试件的破坏模式为局部屈曲破坏或者超低周疲劳破坏,故选取50%混凝土填充率的试件进行参数化分析。有限元分析模型的钢材型号为Q345,翼缘正则化宽厚比Rf的取值范围为0.2~0.8,试件 正 则 化 长细 比的 取 值 范 围为0.25~0.45,轴压比的取值范围为0.1~0.3。研究试件在三种不同加载形式下(合计315 个模型)的裂纹萌生寿命Nf和局部屈曲寿命Nb。试件的翼缘宽度均为256 mm,其余几何尺寸见表2 和表3。试件的翼缘正则化宽厚比Rf和试件正则化长细比-λ 的计算公式如下:

式中:b 为翼缘宽度;t 为板厚;σy为钢材的屈服强度;E 为钢材的弹性模量;ν 为钢材的泊松比;r 为横截面回转半径。
试件“UB20-35C1P1”的编号意义为:UB 表示未加劲箱形截面,20 表示翼缘正则化宽厚比为0.20,35表示试件正则化长细比为0.35,C1表示加载形式为C1,P1 表示施加的竖向荷载为0.1Py,其余编号同理。

表2 试件板厚Table 2 Steel plate thickness of specimens

表3 试件高度Table 3 Height of specimens
2.1 翼缘正则化宽厚比的影响
图3 为轴压比为0.3 时,裂纹萌生寿命随翼缘正则化宽厚比的变化曲线。可以看出,裂纹萌生寿命Nf随着翼缘正则化宽厚比从0.2 至0.8 的递增,呈现出“V 形”走势,先减小后增大。并且“V形”走势的最低点,即在固定试件正则化长细比、轴压比和水平往复加载形式的前提下,使裂纹萌生寿命取到最小值时的翼缘正则化宽厚比均约为0.4。图4 为C3P1 加载形式下试件翼缘正则化宽厚比对裂纹萌生寿命的影响。图中正方形标记为裂纹萌生寿命点。可以看出,翼缘正则化宽厚比为0.4 的试件的累积D 值最先达到1,裂纹萌生寿命最小。这是因为当试件的翼缘正则化宽厚比较小时,随着翼缘正则化宽厚比的增大,钢板厚度减小,沿板厚方向的塑性发展减小,因此钢板表面的塑性累积速度变快,裂纹萌生寿命减小。当试件的翼缘正则化宽厚比较大时,随着翼缘正则化宽厚比的增大,试件越早出现局部屈曲,使得试件的塑性累积速度变慢,裂纹萌生寿命增大。

图3 裂纹萌生寿命随翼缘正则化宽厚比的变化曲线(P3)Fig.3 Crack initiation life versus flange’s normalized width-to-thickness ratio curve(P3)
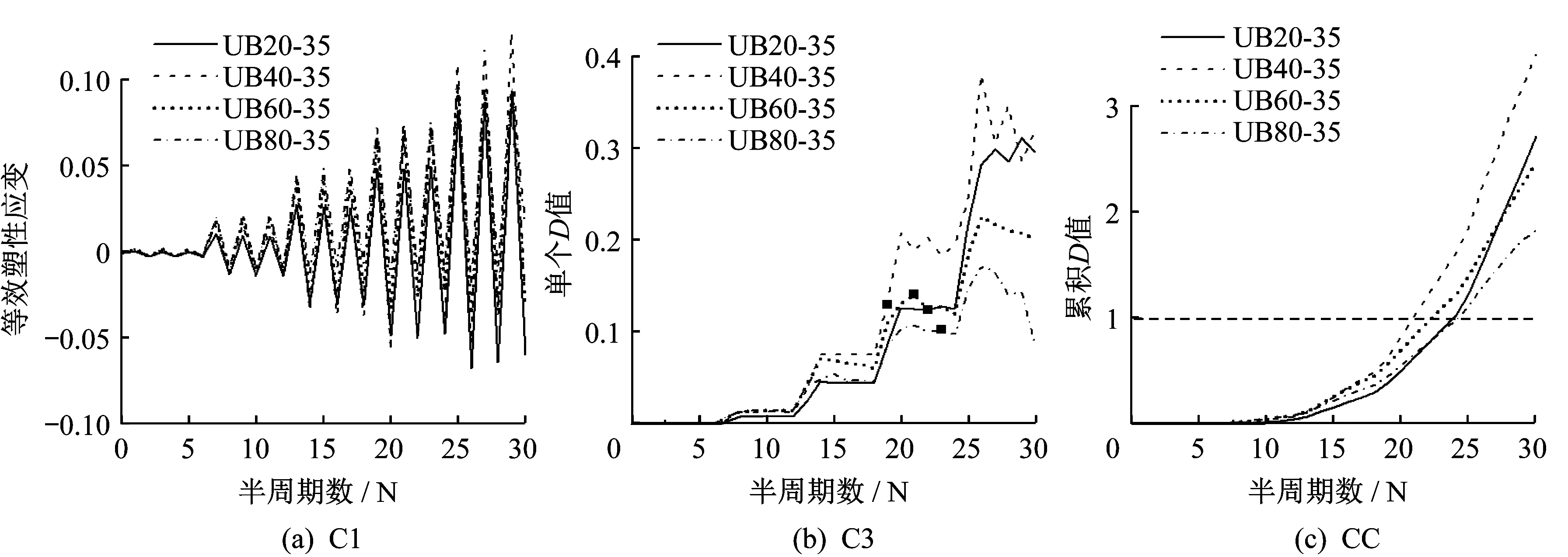
图4 翼缘正则化宽厚比对裂纹萌生寿命的影响(C3P1)Fig.4 Effect of flange’s normalized width-to-thickness ratio on crack initiation life(C3P1)
图5 为轴压比为0.3 时,试件局部屈曲寿命随翼缘正则化宽厚比的变化曲线。可以看出,在试件正则化长细比相同的情况下,局部屈曲寿命都随着翼缘正则化宽厚比的增大而逐步减小。
2.2 试件正则化长细比的影响
图6 为轴压比为0.3 时,裂纹萌生寿命随试件正则化长细比的变化曲线。可以看出,裂纹萌生寿命Nf随着试件正则化长细比从0.25至0.45的递增存在两种较为典型的变化规律。当翼缘正则化宽厚比较小时,裂纹萌生寿命Nf都随着试件正则化长细比的增大而减小;而当翼缘正则化宽厚比较大时,规律反转,裂纹萌生寿命Nf随着试件正则化长细比的增大而增大。图7 为C3P3 加载形式下试件正则化长细比对裂纹萌生寿命的影响。图中三角形标记为局部屈曲寿命点,正方形标记为裂纹萌生寿命点。可以看出,规律发生反转的原因在于对翼缘正则化宽厚比较大的试件,在裂纹萌生之前发生了局部屈曲,使得D 值累积速度变慢,从而导致裂纹萌生寿命Nf随着试件正则化长细比的增大而增大。

图5 局部屈曲寿命随翼缘正则化宽厚比的变化曲线(P3)Fig.5 Local buckling life versus flange’s normalized width-to-thickness ratio curve(P3)
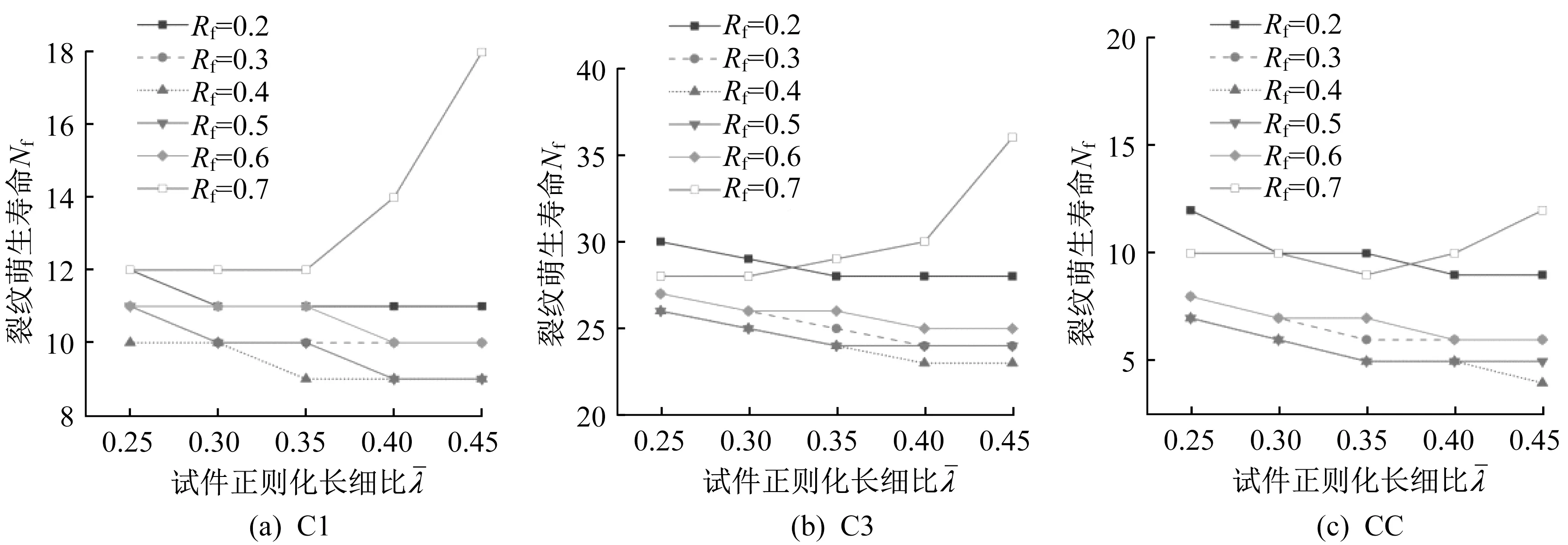
图6 裂纹萌生寿命随试件正则化长细比的变化曲线(P3)Fig.6 Crack initiation life versus specimen’s normalized slenderness ratio curve(P3)
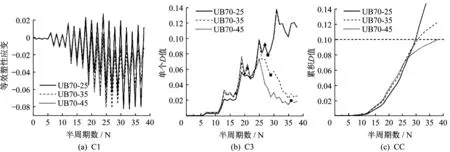
图7 试件正则化长细比对裂纹萌生寿命的影响(C3P3)Fig.7 Effect of specimen’s normalized slenderness ratio on crack initiation life(C3P3)
图8 为轴压比为0.3 时,局部屈曲寿命随试件正则化长细比的变化曲线。可以看出,在翼缘正则化宽厚比相同的情况下,局部屈曲寿命都随着试件正则化长细比的增大而逐步减小。
2.3 轴压比的影响

图8 局部屈曲寿命随试件正则化长细比的变化曲线(P3)Fig.8 Local bucking life versus specimen’s normalized slenderness ratio curve(P3)
图9 为试件正则化长细比为0.35 时,不同轴压比下试件的裂纹萌生寿命和局部屈曲寿命比较。可以看出,轴压比越大的试件,其裂纹萌生寿命越大。图10 为“UB80-25C3PX”试件组的轴压比对裂纹萌生寿命的影响。轴压比越大,对应的水平屈服位移越小,桥墩根部附近的塑性应变幅也越小,使得每个半周期的单个D值变小,因此需要更多的周期来累积D 值至1,即裂纹萌生寿命变大。

图9 不同轴压比下试件的裂纹萌生寿命和局部屈曲寿命比较Fig.9 Comparison of crack initiation life and local buckling life of the specimens under different axial load ratios
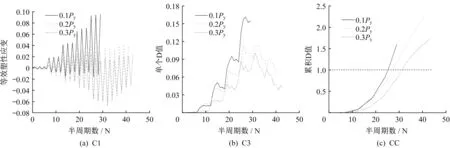
图10 轴压比对裂纹萌生寿命的影响Fig.10 Effect of axial load ratio of the specimens on crack initiation life
由图9 可以看出,在翼缘正则化宽厚比相同的情况下,试件局部屈曲寿命随着轴压比的增大而减小或保持不变。随着轴压比的增大,水平屈服位移变小,因此即使局部屈曲寿命保持不变,试件的极限位移仍随轴压比的增大呈减小趋势。
3 钢桥墩破坏模式的确定方法
基于对315 个试件的参数化分析结果,通过数据拟合方法分别得到在C1、C3 和CC 三种加载形式下的裂纹萌生寿命Nf和局部屈曲寿命Nb的预测公式如下,公式中的系数如表5 所示。轴压比为0.3时,三种不同加载形式下预测公式的拟合情况如图11 和图12 所示,可以看出,预测公式能够较好地反映有限元模拟结果的变化趋势。

式中,a,b,c,d,A,B,C,D为拟合公式系数。
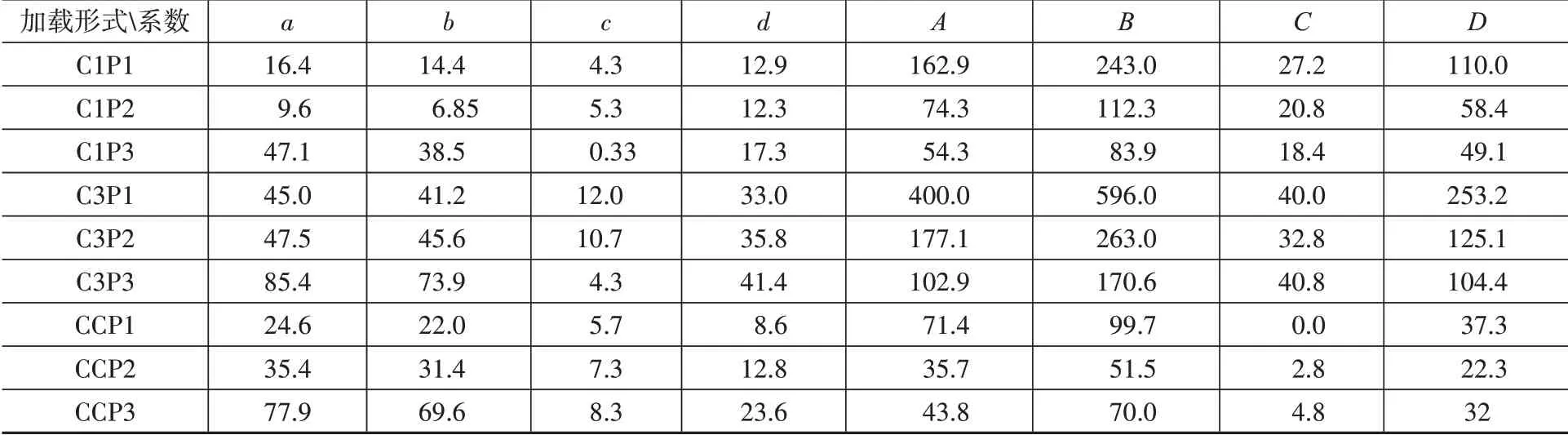
表5 式(6)和式(7)中的系数列表Table 5 Coefficient list in formulas(6)and(7)
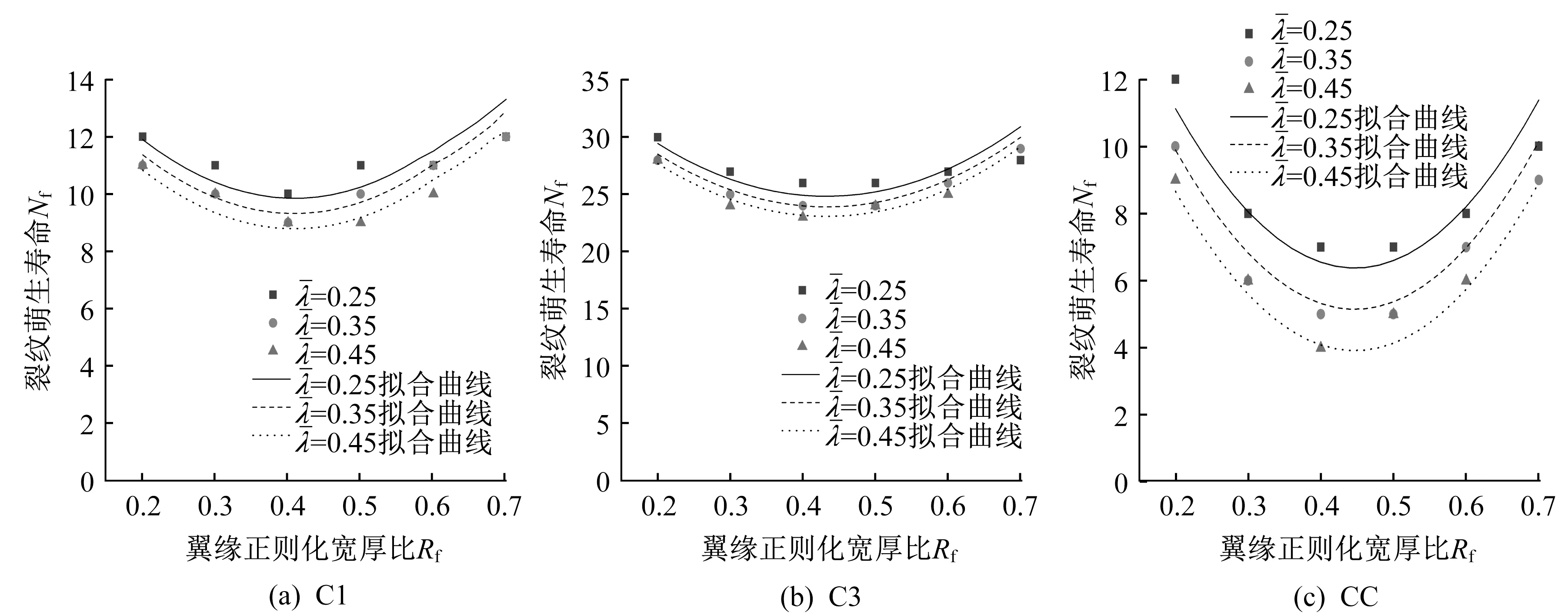
图11 三种不同加载形式下裂纹萌生寿命预测公式的拟合情况Fig.11 Fitting of crack initiation life prediction formulas under three kinds of loading patterns
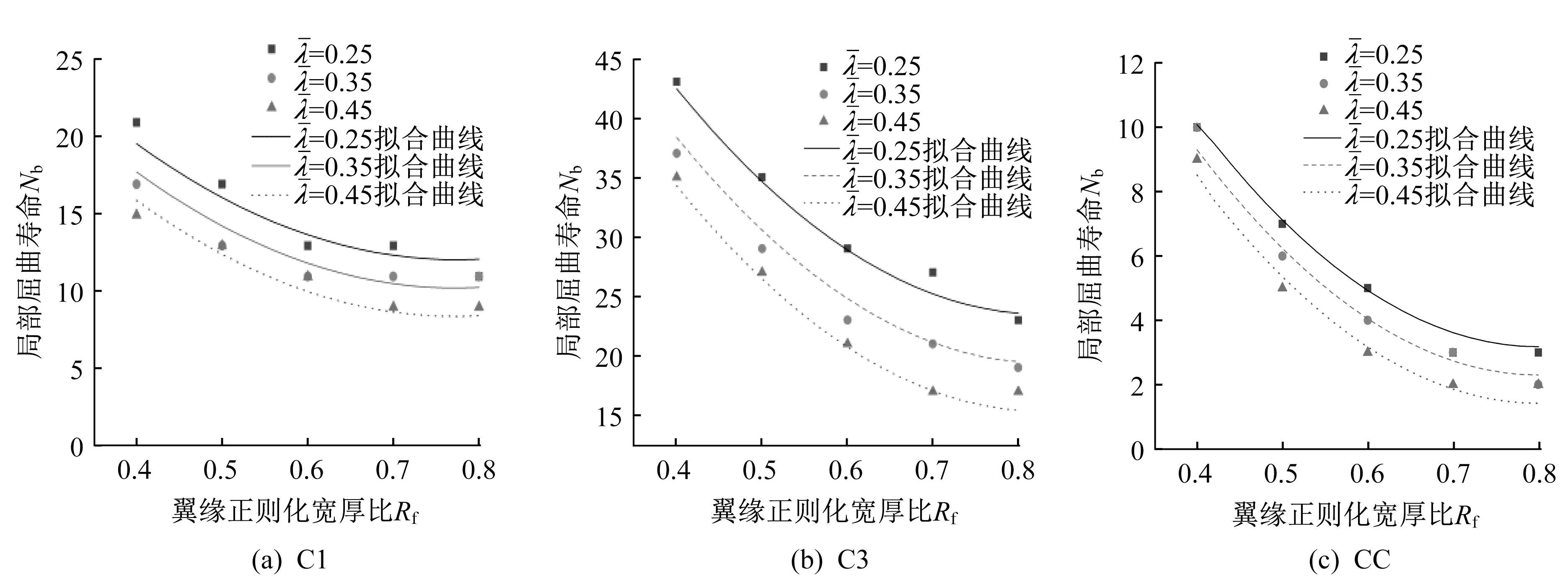
图12 三种不同加载形式下局部屈曲寿命预测公式的拟合情况Fig.12 Fitting of local buckling life prediction formulas under three kinds of loading patterns
研究试件的破坏模式时,应该同时考虑超低周疲劳破坏和局部屈曲破坏两种破坏模式。通过比较试件的裂纹萌生寿命和局部屈曲寿命,选择两种寿命中的较小值,作为判断试件实际破坏模式的依据。图13 为试件正则化长细比为0.45,轴压比为0.3时,裂纹萌生寿命和局部屈曲寿命随翼缘正则化宽厚比的变化情况。可以发现,对于翼缘正则化宽厚比较小的试件,如Rf=0.2 或Rf=0.3,破坏模式以超低周疲劳破坏为主;而对于翼缘正则化宽厚比较大的试件,如Rf=0.7 或Rf=0.8,破坏模式以局部屈曲为主。对于翼缘正则化宽厚比处于两者之间的试件,需要利用式(6)和式(7)分别计算试件的裂纹萌生寿命和局部屈曲寿命,通过比较两种寿命的大小,才能准确确定钢桥墩的实际破坏模式。
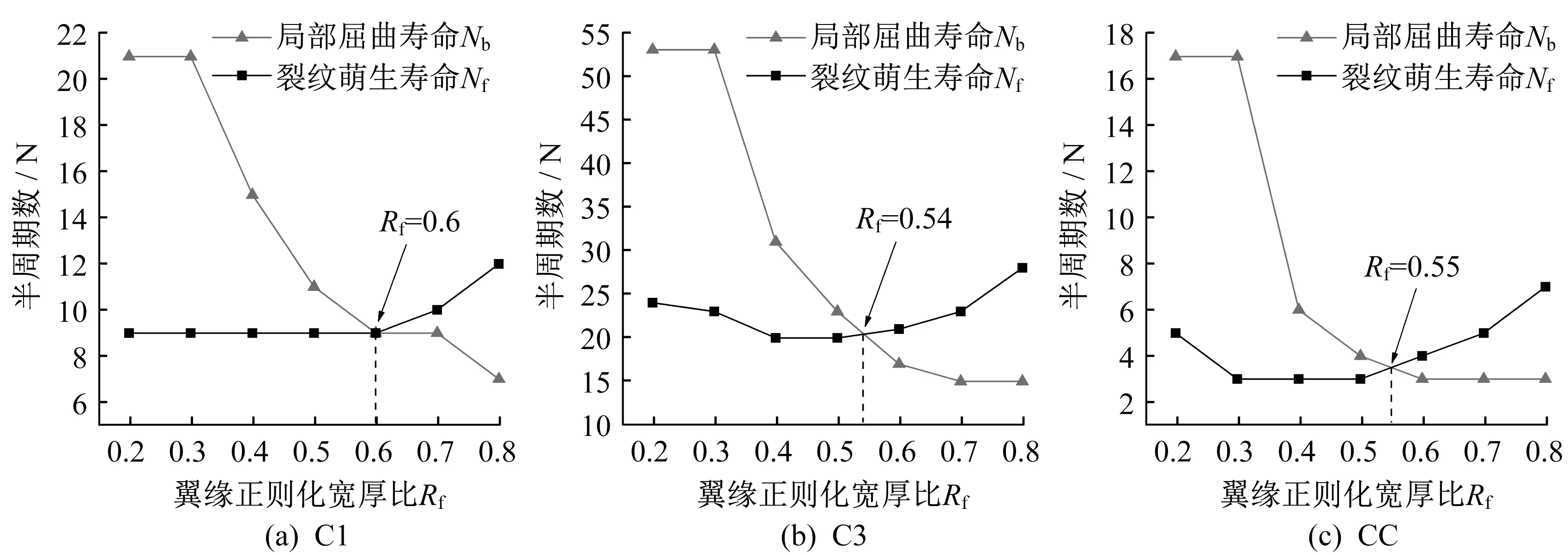
图13 三种加载形式下的试件实际破坏模式确定Fig.13 Determination of actual failure modes of the specimens under three kinds of loading patterns
4 结 论
(1)随着翼缘正则化宽厚比的增大,试件的超低周疲劳裂纹萌生寿命呈现先减后增的“V 形”走势,而局部屈曲寿命都呈现递减趋势。
(2)由于局部屈曲对试件损伤累积的影响,试件正则化长细比对裂纹萌生寿命的影响存在两种典型的变化规律。当翼缘正则化宽厚比较小时,裂纹萌生寿命都随着试件正则化长细比的增大而减小;而当翼缘正则化宽厚比较大时,裂纹萌生寿命则随着试件正则化长细比的增大而增大。局部屈曲寿命都随着试件正则化长细比的增大而减小。
(3)随着轴压比的增大,对应的水平屈服位移变小,桥墩根部附近的塑性应变幅也逐渐减小,导致裂纹萌生寿命变大。局部屈曲寿命都随着轴压比的增大而减小或保持不变。
(4)对于翼缘正则化宽厚比较小的试件,破坏模式以超低周疲劳破坏为主;对于翼缘正则化宽厚比较大的试件,破坏模式以局部屈曲为主。
(5)本文基于参数化分析结果,分别拟合了部分填充混凝土箱形截面钢桥墩的裂纹萌生寿命和局部屈曲寿命预测公式,并提出了钢桥墩破坏模式的确定方法,可为钢桥墩的延性设计提供理论依据。

