梁腹板削弱型节点滞回性能研究

刘盼盼 张海风 贺海洋

（商丘学院应用科技学院土木建筑系，开封475000）

0 引 言

在地震作用下，最常见的破坏发生在节点处，使结构抗震性能不能满足要求［1］。1995 年，日本阪神地震中大量焊接节点焊缝处发生了脆性破坏［2］，为了减小焊缝处破坏的风险，国内外开始研究节点。通过削弱梁翼缘，可以实现塑性铰外移，提高了节点的延性，但是导致了梁平面外的刚度下降，从而使梁易出现平面外失稳的现象。Wilkinson［3］为决RBS（狗骨式削弱型节点）导致平面外刚度下降的问题，提出了一种楔形削弱节点。焊接节点削弱形式为梁翼缘削弱和梁腹板开洞，但对削弱梁腹板高度的节点研究甚少。

1 有限元模型建立与验证

对已有梁翼缘削弱型节点的试验［4，5］进行数值模拟，主要包括建立模型尺寸、定义材料属性、选择单元类型等方面。

1.1 有限元模型的建立

1.1.1 试验试件几何尺寸与材料属性

试件选取文献［5］中的ST-2 试件，如图1所示。

图1 ST-2节点连接的构造详图（单位：mm）Fig.1 Details of construction of ST-2 node connections（Unit：mm）

柱子截面尺寸为HW200×200；腹板和翼缘厚度分别为8 mm 和12 mm；梁的截面尺寸为HN300×150；腹板和翼缘厚度分别为6.5 mm 和9 mm。a 为试件削弱部分的起点至柱面距离，取110 mm（0.73bf）；b 为削弱部分的长度，取240 mm（0.8hb）；其中，bf为梁的翼缘宽度，hb为梁截面高度。为了方便施焊，在梁腹板的上下角处切割成弧形切口，弧形切口的半径取35 mm，焊接孔处切口形状如图1（a）所示。

试件中梁与柱的材料选用的是Q235 热轧H型钢，各板件力学性能见表1。材料采Von Mises屈服准则，为各向同性材料。

1.1.2 网格的划分

模型采用实体单元，首先对实体进行了切割，对于节点域与削弱部分处加密了网格的划分［6］。网格单元采用的类型为C3D8I，网格划分的结果如图2所示。

表1 ST-2试件的材料属性Table 1 Material properties of ST-2 specimens

图2 ST-2节点网格划分Fig.2 Mesh generation of ST-2 joint

1.1.3 试验的加载装置以及加载方案

在ABAQUS 模拟中，梁与柱子采用tie 连接。柱上下端均采用固定约束，距离柱子1 m 处施加梁侧向约束，梁端施加循环荷载。在试验中，具体试验装置采用拟静力方案。柱子下端通过放置H型钢，通过使用高强螺栓与地面进行连接，柱子上端与下端均通转换梁与反力墙连接，在离柱子一定距离的梁处设置梁的侧向支撑。通过采用MTS液压伺服器对梁端部施加低周循环荷载，试验装置如图3和图4所示。

图3 ST-2试件试验加载装置（单位：mm）Fig.3 Test loading device of ST-2 specimen（Unit：mm）

图4 ST-2试件试验加载图Fig.4 Test loading diagram of ST-2 specimen

ABAQUS 有限元采用位移加载的方式，位移加载方式能更好地收敛，在有限元模拟中是常用的加载方式。在屈服前，加载位移采用屈服位移的20%、40%、60%、80%，每级循环一次。屈服后，按照屈服位移的1 倍、2 倍、3 倍、4 倍进行循环的加载，每级循环2次，如图5所示。

图5 加载制度Fig.5 Loading system

1.2 有限元结果与试验结果的分析

1.2.1 破坏状态的对比

试验中，梁翼缘的端部首先发生屈服，随之梁翼缘削弱部分也开始出现屈服。当荷载为70.3 kN，梁端发生转角，梁端翼缘开始屈服。当荷载达73.1 kN 时，梁翼缘削弱最深处开始屈服。当达到91.8 kN，在削弱部分出现了明显的塑性铰。当荷载达到101.1 kN 时，试件达到了极限荷载。随后，梁产生较大的扭转从而停止加载。在试验中，尽管设置了侧向支撑但不能有效防止梁的侧向失稳。模拟中，由于边界条件理想化，梁未发生整体的扭转失稳，对比如图6所示。

图6 可知，模拟的梁翼缘与腹板削弱处出现了屈曲现象，与试验状态基本一致。两种结果都表明了塑性铰的位置均出现在削弱部分，实现远离焊缝的目的。

图6 试验与有限元破坏状态对比Fig.6 Comparison of failure state between test and finite element method

1.2.2 滞回曲线与承载能力的对比

图7为试验与有限元得到的滞回曲线结果，滞回曲线都比较饱满，构件具有很好的滞回性能。有限元得到的曲线更加饱满，原因是有限元没有考虑焊缝以及钢材存在的初始缺陷以及残余应力等。

图7 滞回曲线对比图Fig.7 Hysteresis curve comparison diagram

通过滞回曲线得到承载能力结果如表2所示，试件ST-2试验的极限荷载为101.1 kN，有限元模拟的极限荷载为89.71 kN，误差为11%。主要原因是试验中附加的边界条件的约束力要强于有限元。试验的延性系数为4.6，有限元的延性系数为4.2，误差为8.7%。通过对比破坏形态、滞回性能和承载能力，误差不大，证明了有限元模拟的有效性。

表2 试验与有限元结果对比Table 2 Experimental and finite element resultscontrast

2 梁腹板削弱型节点

2.1 节点设计

2.1.1 细部构造设计

梁尺寸为HN300×150×9×6.5，长度为1 500 mm，柱子尺寸为HW200×200×8×12，长度为1 400 mm。梁柱均采用焊接的方式，传统节点选自文献［4］中ST-6 试件。参考文献［7］中的削弱尺寸，a=hb-1.25hb，b=0.17hb-0.21hb，c=0.83hb-0.92hb，其中，hb为梁高。a为削弱中点位置至柱面距离，取335 mm；b表示削弱部分的深度，取50 mm；c为削弱最深处起点位置与柱子之间的距离，取200 mm。加强板尺寸为176 mm×500 mm×8 mm，加强板上下分别多出加劲肋100 mm。采用两种不同尺寸的加劲肋，加劲肋1 尺寸176 mm×96 mm×10 mm，加劲肋2 尺寸为176 mm×88 mm×10 mm。为了方便梁翼缘的施焊，在梁腹板的上下角处切割成弧形切口，弧形切口的半径取35 mm。通过软件对三角形削弱型节点（NTWJ）、折线削弱型节点（NLWJ）、圆形削弱型节点（NRWJ）和传统节点（TWJ）的破坏状态、承载能力等进行对比，节点如图8所示。

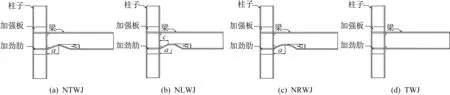
图8 节点细部构造图Fig.8 Node detail construction diagram

2.1.2 加载制度

柱子上下端未施加轴向力，上下端固定，梁侧施加侧向支撑，梁端耦合一点，在耦合点施加循环位移，初始位移取屈服位移的20%，屈服前每级荷载循环1 次，每级每次增加位移为20%。屈服后，每级位移取屈服位移1 倍、2 倍、3 倍、4 倍，每级荷载循环3 次。首先对四种节点在梁端进行单调加载，单调荷载作用得到屈服位移均在21 mm左右。

2.2 有限元计算结果对比分析

2.2.1 破坏状态的对比

如 图9-图12 所 示，依 次 为NTWJ、NLWJ、NRWJ、TWJ 四种节点在位移荷载作用下屈曲状态、峰值状态以及极限状态下的Mises 应力云图。

从图9、图10 可知，NTWJ 与NLWJ 在屈服状态时，最大应力出现在梁翼缘削弱最深处，梁其他部分还处于弹性阶段；随梁端位移的增加，其他部分达到屈服，梁上塑性区域不断扩大，节点进入到塑性状态；当位移继续增加，梁腹板和下翼缘削弱部分进入到强化阶段；当达到峰值状态时，塑性铰开始形成；在极限状态时，梁上翼缘与梁腹板出现屈曲变形，最终由于局部鼓屈而破坏。

从图11、图12 可知，NRWJ 与TWJ 在达到屈服状态时，梁端焊接弧口处首先达到屈服状态；随着梁端位移增加，节点域梁端大部分开始屈服，处于塑性状态；当达到峰值状态时，塑性铰形成，但塑性铰出现在焊缝区域；当位移加载极限时，焊缝处发生破坏，塑性铰均出现在焊缝处。因此，四种节点中，NTWJ和NLWJ均能实现塑性铰的外移。

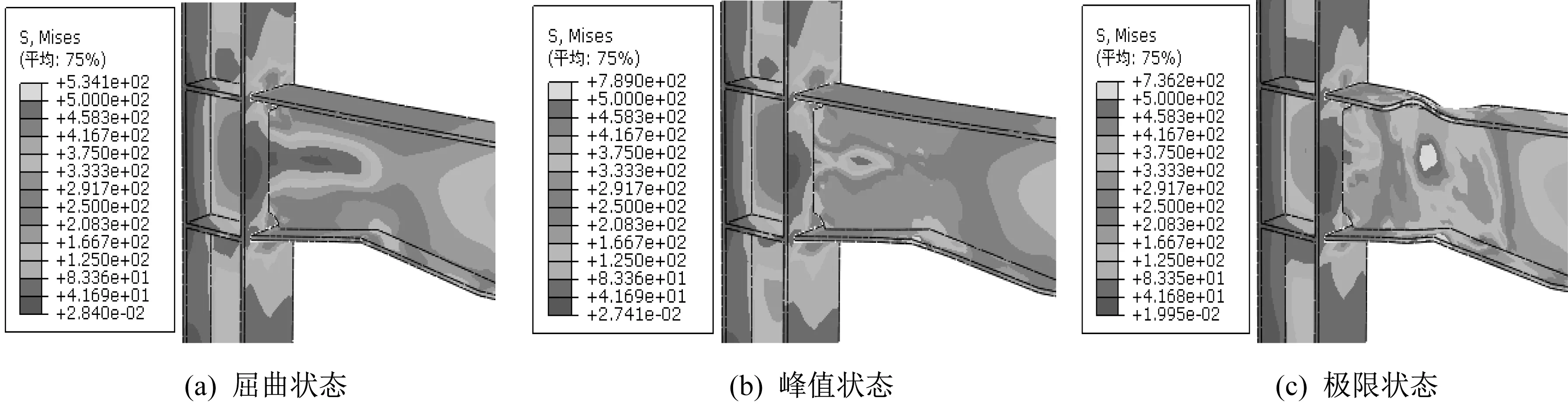
图9 NTWJ的Mises应力云图Fig.9 Mises stress cloud of NTWJ

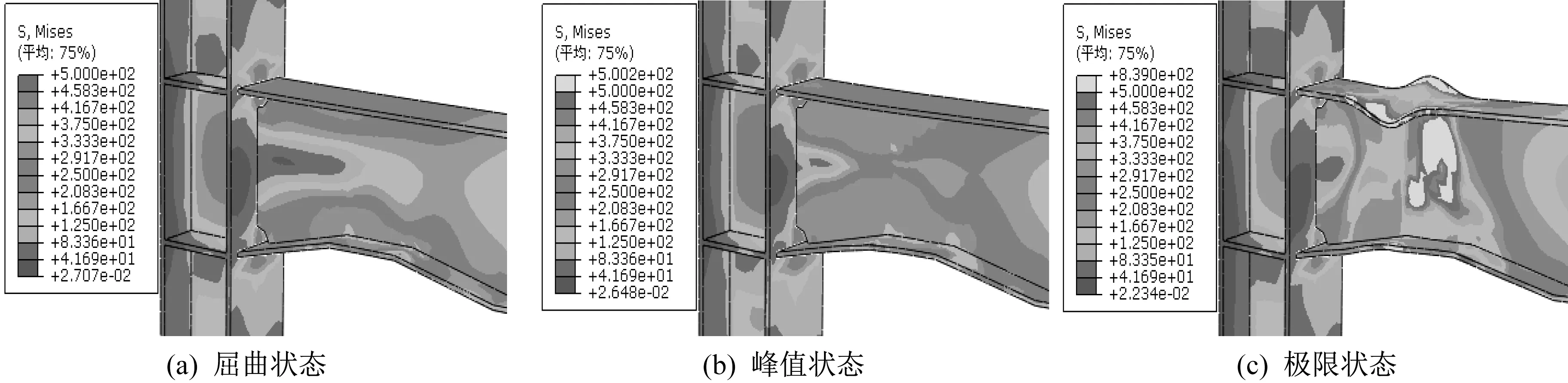
图10 NLWJ的Mises应力云图Fig.10 Mises stress cloud of NLWJ

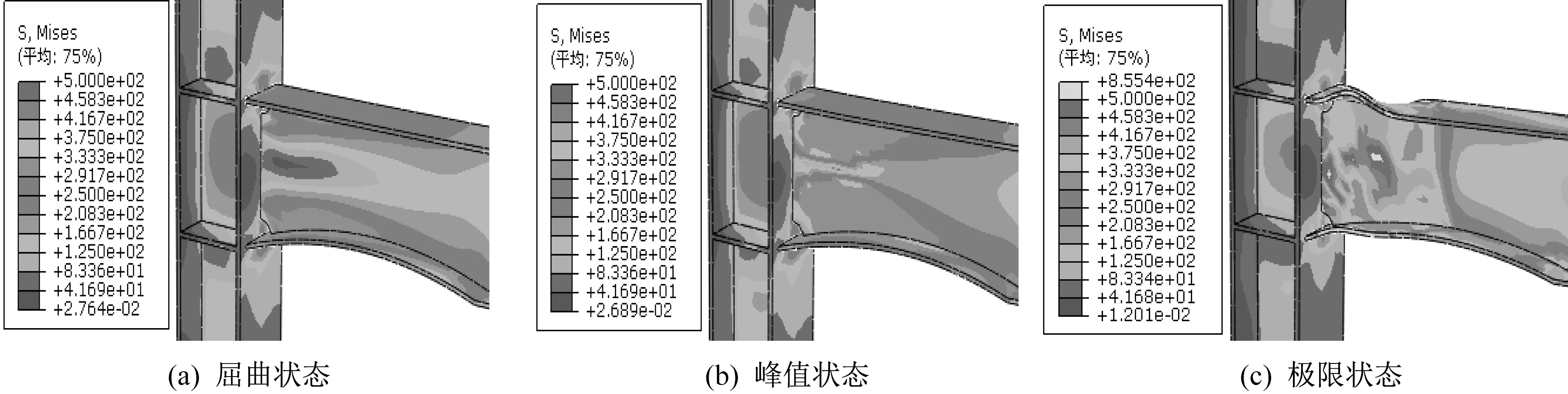
图11 NRWJ的Mises应力云图Fig.11 Mises stress cloud of NRWJ

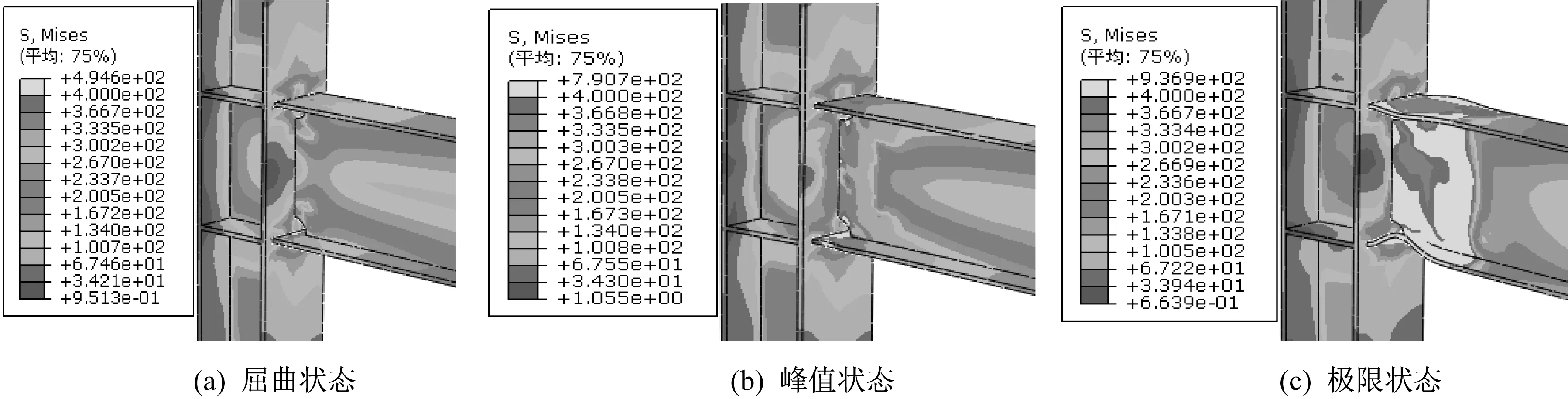
图12 TWJ的Mises应力云图Fig.12 Mises stress cloud of TWJ

2.2.2 滞回曲线的对比

图13 为NTWJ、NLWJ、NRWJ 和TWJ 的滞回曲线。

图13中，NLWJ滞回曲线最饱满，TWJ的滞回曲线出现捏缩的现象。在加载初期，梁处于弹性阶段，滞回环面积很小，当加载位移至42 mm 前，NLWJ 与NRWJ 滞回曲线相接近，均优于NTWJ。当加载位移大于42 mm，NTWJ 和NRWJ 的滞回曲线开始出现明显的不对称，负位移作用下滞回性能比正位移作用下滞回性能差。四种节点的滞回曲线在梁端位移加载过程中，斜率随着位移加载的增加而减小，说明刚度发生了退化，当达到极限荷载，滞回曲线逐渐出现下降段，直至试件破坏。NLWJ 的滞回曲线最饱满，说明抗震性能最好，三种削弱节点滞回曲线均比TWJ 饱满，耗能能力均优于TWJ。

图13 滞回曲线对比Fig.13 Hysteresis curve comparison

2.2.3 骨架曲线的对比

骨架曲线如图14 所示，在加载初期，节点处于弹性阶段，骨架曲线按照一定的曲率上升，四种节点的初始刚度基本相同；随着位移的继续增大，节点进入弹塑性阶段，曲线的斜率逐渐减小，直到达到顶峰荷载，随之出现了塑性铰，斜率逐渐成为负斜率，最终试件破坏。不管是正位移还是负位移作用下，TWJ 最早达到峰值荷载，并且TWJ 节点峰值荷载最大；对于正向位移，三种削弱节点的峰值荷载NTWJ>NLWJ>NRWJ。但对于负向位移，NTWJ 和NRWJ 节点的承载力下降明显，而NLWJ 的骨架曲线下降缓慢。综合对比分析，NLWJ 相对于其他节点比较稳定，承载能力和耗能能力最优。

2.2.4 延性系数和承载能力的对比

通常采用延性系数来判断结构的延性特性，延性系数的定义为结构体系极限位移Δu与屈服位移Δy之比［8］。用公式表达为

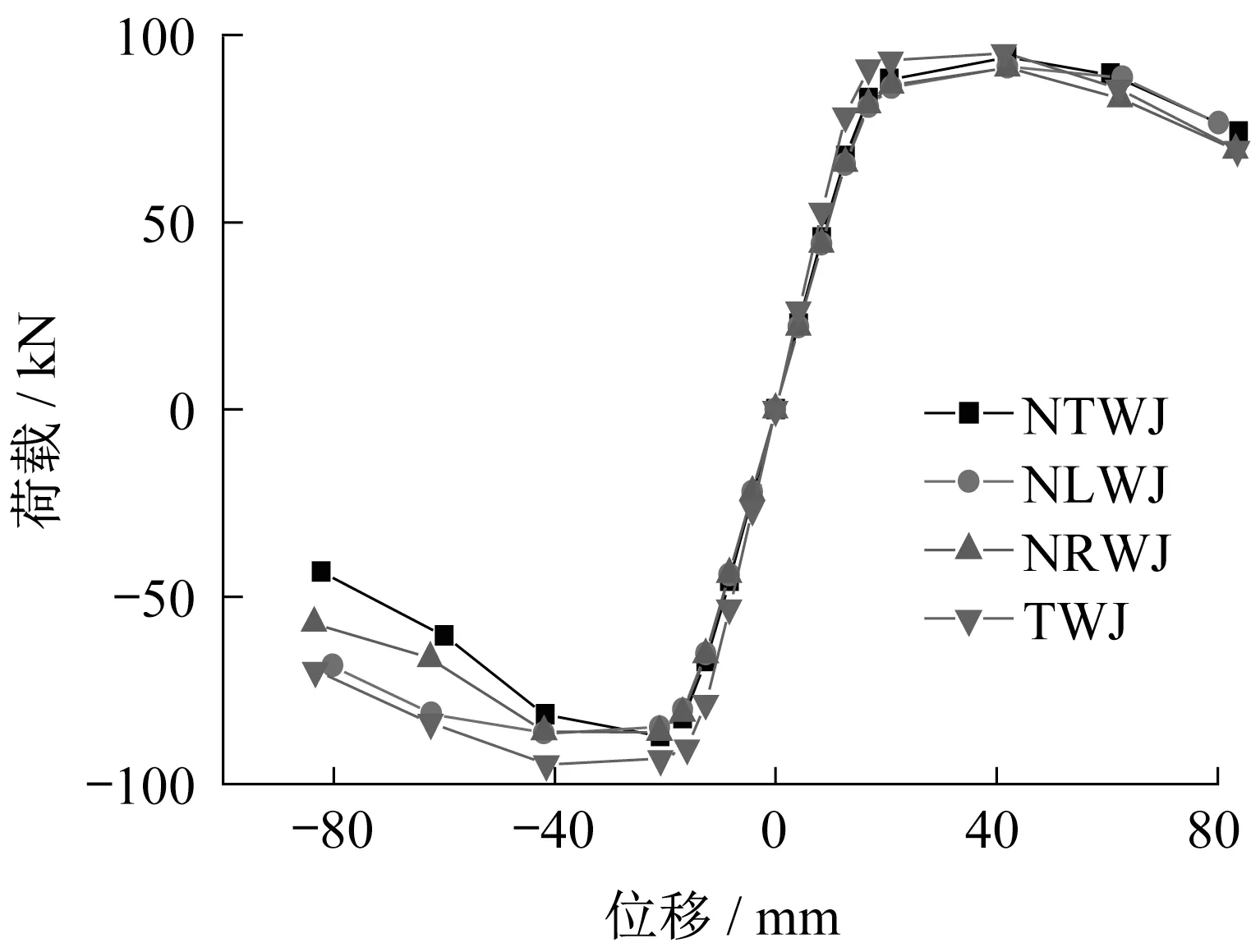
图14 骨架曲线对比Fig.14 Skeleton curve contrast

表3 中，在正位移下，NTWJ、NLWJ、NRWJ 的屈服荷载、峰值荷载和极限荷载对于TWJ 均有所下降，下降程度均小于6%。承载力大小是TWJ>NTWJ>NLWJ>NRWJ，延性系数排序为NTWJ>NLWJ>NRWJ>TWJ，三种削弱节点的延性系数均大于TWJ。其中NLWJ 的延性系数比TWJ 大，相差百分比为25.9%。

表3 正位移作用下的承载力以及延性系数的对比Table 3 Comparison of the bearing capacity and ductility coefficient under the action of positive displacement

表4，在负位移下，NTWJ、NLWJ、NRWJ 承载能力比TWJ 降低，下降程度小于11%，承载力大小为TWJ>NLWJ>NTWJ>NRWJ，延性系数大小为NLWJ>NRWJ>TWJ>NTWJ，NLWJ 的延性系数比TWJ 大，相差百分比为30.3%。在负位移作用下，NTWJ 承载力以及延性系数明显下降，承载力和延性系数均小于TWJ。

因此，削弱对节点的承载力有一定的影响。在正位移下，三种削弱节点的承载力相比TWJ小，延性系数都有所提高。在负位移作用下，NTWJ 与NRWJ 的承载力以及延性系数下降。但NLWJ 承载力下降不多，反而能更大地提高节点的塑性变形能力。因此四种节点中，NLWJ最优。

表4 负位移作用下的承载力以及延性系数的对比Table 4 Comparison of the bearing capacity and ductility coefficient under the action of negative displacement

2.2.5 刚度退化曲线的对比

刚度退化指在低周荷载的作用下试件的刚度退化的性能，刚度退化采用割线刚度K 来表示，K的计算公式采用式（2）计算［8］。式中，F+，F-为在相同滞回峰值点的正、负荷载，Δ+，Δ-表示为同一个滞回环峰值点的正、负位移，与正、负荷载相对应。刚度退化曲线的结果如图15所示。

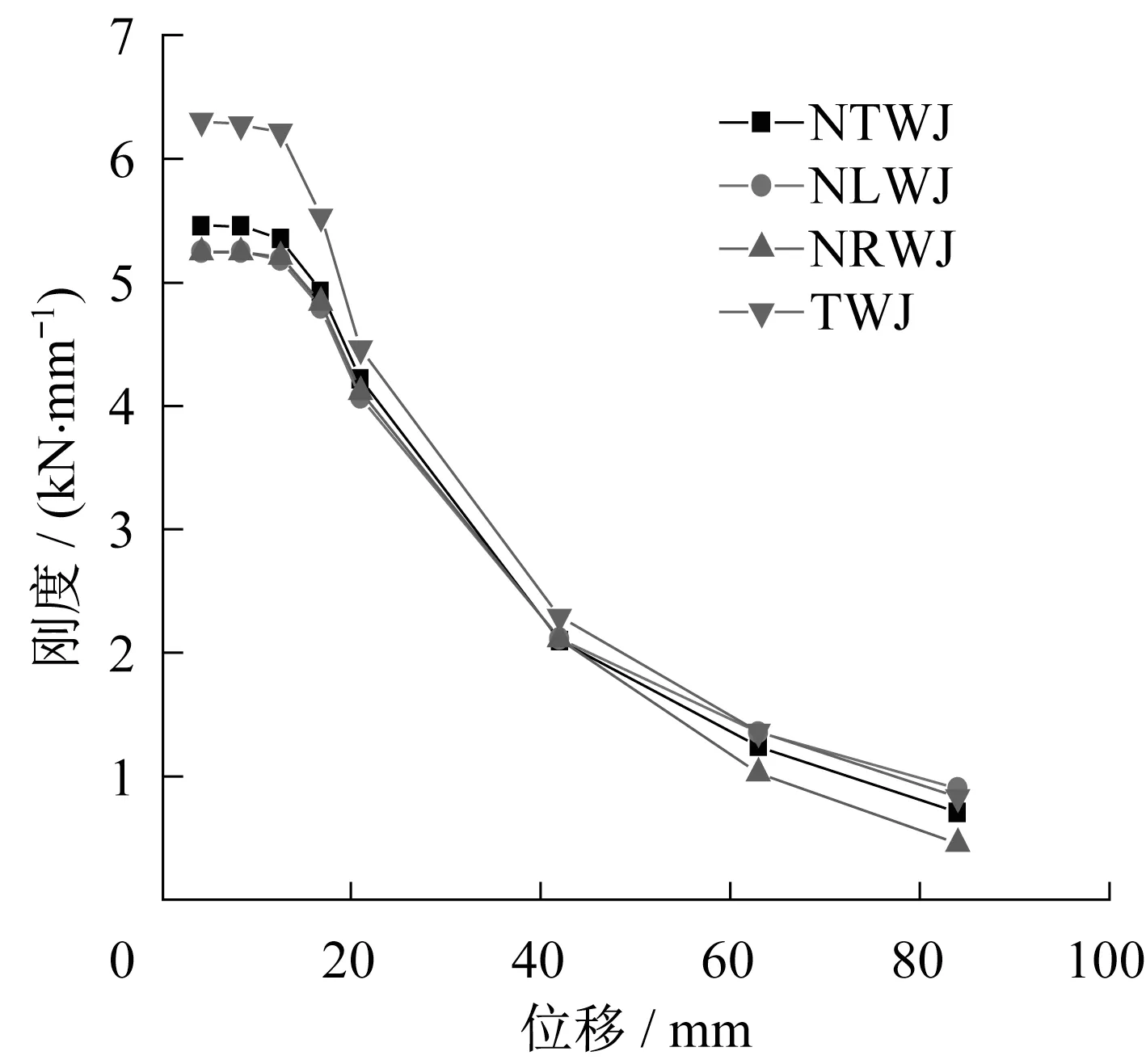
图15 刚度退化曲线对比Fig.15 Stiffness degradation curve comparison

从图15 可知，当梁端施加较小的位移时，节点刚度下降曲线基本为水平线，表明弹性阶段内基本无刚度退化现象；随着位移增加，四种节点刚度缓慢下降。TWJ 在弹性阶段，刚度大于三种削弱节点。随着位移的增加，TWJ 刚度下降速度最快；随着位移增大，NTWJ 与NLWJ 的塑性铰在梁腹板削弱处形成，刚度退化的速度减小。但NRWJ 在加载后期刚度退化速度最快，主要原因是塑性铰发生在焊缝处。因此，从刚度退化的比较来说，TWJ 刚度大，退化速度快，三种削弱节点刚度退化相比较而言，NLWJ 刚度下降速度最缓慢，表明NLWJ的延性最优。

2.2.6 关键部位应力路径的对比

选取各模型在梁端加载位移达至84 mm时的应力路径值进行对比，此时各模型处于极限应力状态。关键应力路径包括两条：路径一，梁上翼缘焊缝处；路径二，梁下翼缘焊缝处。

（1）路径一的Mises应力分布

首先分析梁上翼缘焊缝处的应力分布情况，分别分析试件在+84 mm（位移向上）（图16）和-84 mm（位移向下）（图17）时的应力分布。

图16 +84 mm时沿上翼缘Mises应力路径分布Fig.16 The specimens followed the Mises stress path along the upper flange at+84 mm

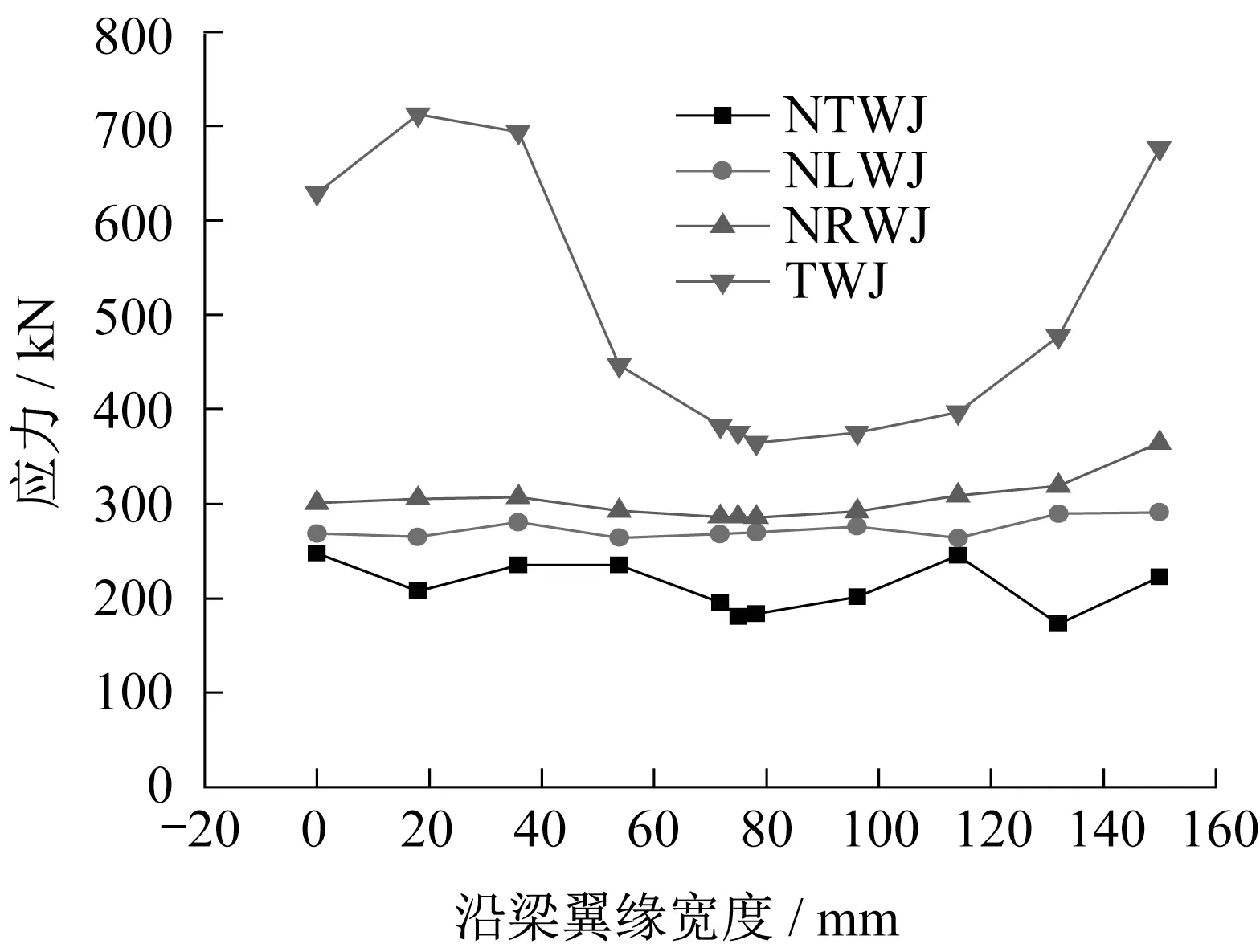
图17 -84 mm时沿上翼缘Mises应力路径分布Fig.17 The specimens followed the Mises stress path along the upper flange at-84 mm

图16 可知，在梁端位移达到+84 mm 时，NTWJ、NLWJ 和TWJ 节点基本呈现对称分布，NRWJ 应力呈现了不对称分布，原因是梁出现了扭转现象。NRWJ 应力最大，最大应力超过材料极限强度443.3 MPa。NTWJ、NLWJ 与TWJ 相比，减小了梁上翼缘的焊缝处应力。其中NLWJ 应力值均小于其屈服强度值281.1MPa。对比可知，NLWJ和NTWJ均能实现塑性铰外移。

由图17 可知，在梁端位移达-84 mm 时，TWJ应力值远大于削弱节点的极限应力值，三种削弱节点的应力小于极限应力。其中NTWJ 与NLWJ应力均小于屈服强度。因此，NTWJ和NLWJ在位移达到84 mm 时均能减小梁翼缘焊缝处应力，减小焊缝脆性破坏。

（2）路径二的Mises应力分布

应力路径二为梁下翼缘焊缝处。分别分析试件在+84 mm（位移向上）（图18）和-84 mm（位移向下）（图19）时的应力分布。

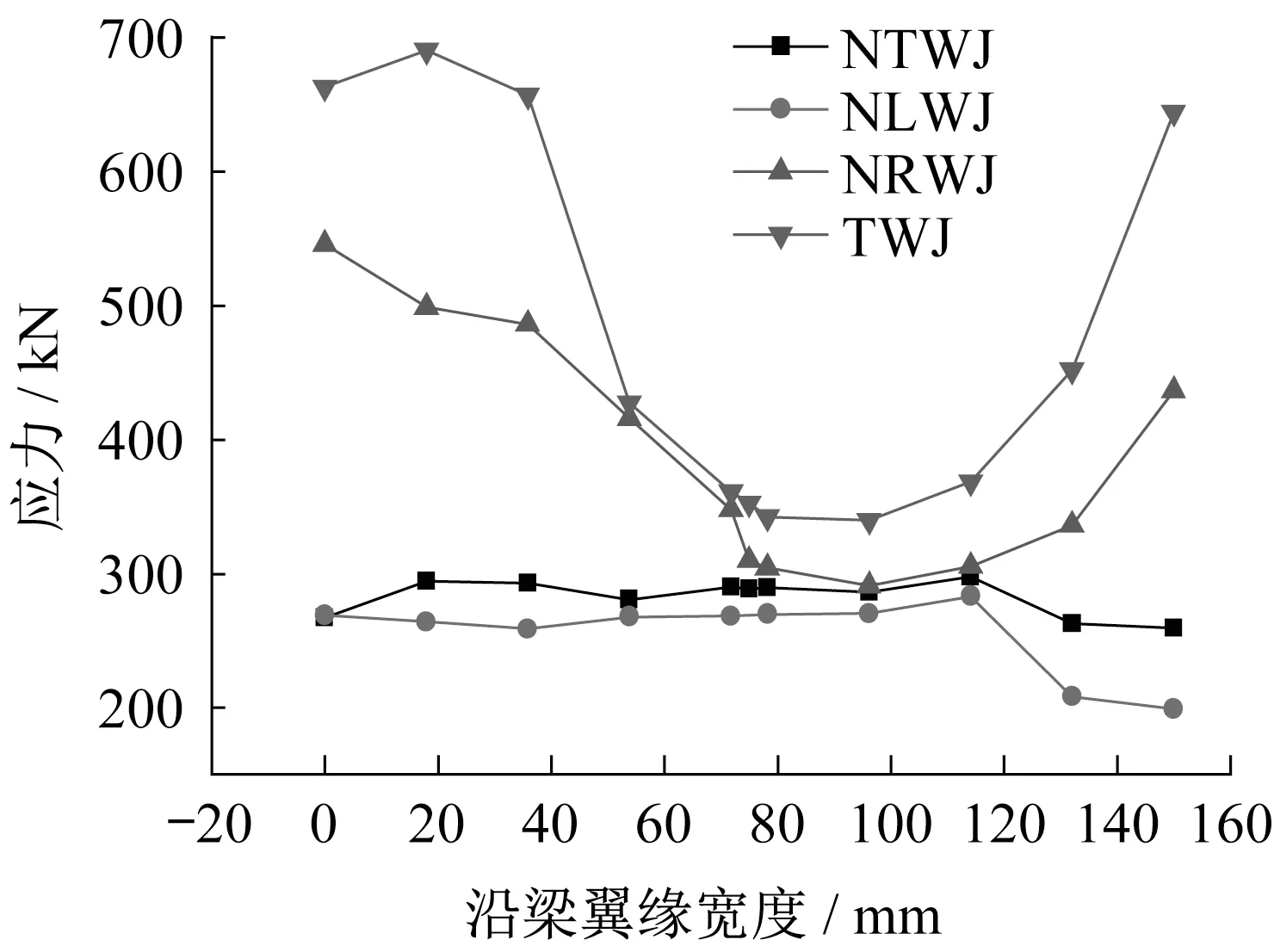
图18 +84 mm时沿下翼缘Mises应力路径分布Fig.18 The specimens followed the Mises stress path along the lower flange at+84 mm

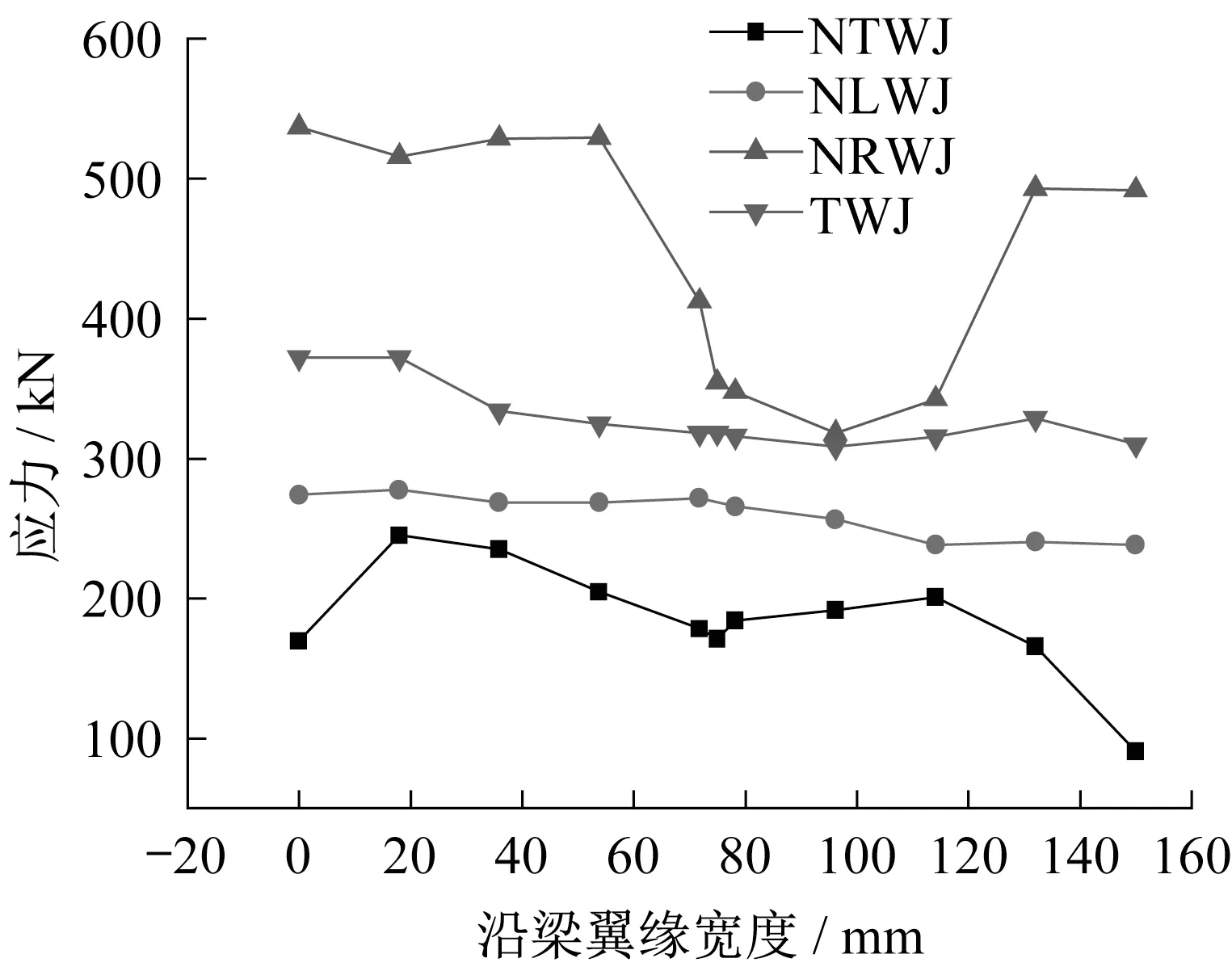
图19 -84 mm时沿下翼缘Mises应力路径分布Fig.19 The specimens followed the Mises stress path along the lower flange at-84 m

图18 可知，当位移加载至+84 mm 时，下翼缘应力呈现基本对称现象。对比图16 和图18，NTWJ 和NLWJ 梁下翼缘焊缝应力小于梁上翼缘焊缝应力。NTWJ 和NLWJ 下翼缘焊缝处的应力减小。而NRWJ 焊缝应力大于材料极限强度，不能实现塑性铰外移。

图19 中，-84 mm 时TWJ 应力值大于极限强度。三种削弱型节点的应力均小于极限强度。因此，无论是在+84 mm或-84 mm，NTWJ和NLWJ的应力值均小于极限强度并且小于NRWJ 和TWJ，能实现塑性铰外移，减小焊缝破坏的风险。

3 结 论

采用ABAQUS 软件对四种节点进行了模拟，研究结果表明：

（1）三角形削弱型节点和折线削弱型节点可以实现塑性铰的外移，而圆形削弱型节点不能实现塑性铰的外移。

（2）四种节点中，削弱节点滞回曲线饱满，表明了节点具有很好的耗能能力。其中折线削弱型梁柱节点的滞回性能最佳。

（3）承载力方面，折线削弱型节点相对于传统节点下降程度小于11%，但延性系数大于26%。表明折线削弱型节点承载力下降不多，但大大提高节点延性。