钢板-混凝土组合连梁受剪承载力概率模型分析
吕贝贝 谭朝明 刘 喜
(1.山西大同大学建筑与测绘工程学院,大同037003;2.长安大学建筑工程学院,西安710061)
0 引 言
与普通连梁相比,钢板-混凝土组合(PRC)连梁由于内嵌钢板的作用,而显著提高了其抗剪承载能力和耗能能力,可实现弯曲破坏,提高构件抗震性能。目前,国内外关于PRC 连梁抗剪性能进行了一些试验分析和理论研究,为工程设计提供了重要依据。张刚[1]设计了6 个PRC 连梁的往复加载试验,试验表明,混凝土连梁中配置钢板不仅可以提高连梁的抗剪承载力,改善其延性,还可以避免连梁发生弯曲滑移破坏;Lam[2]完成了8 个PRC连梁试件的低周载荷试验,考虑了跨高比、配筋率、钢板尺寸等的影响;史庆轩等[3]进行了7 根小跨高比PRC 连梁试件的拟静力试验,研究了连梁跨高比、钢板配钢率以及楼板等因素对其抗震性能的影响;Cheng[4]进行了16 个PRC 连梁的单调载荷试验,并提出了对角剪切破坏模型和剪切粘结破坏模型。但试验资料还很欠缺,尚没有较好的统一计算模型和方法。
近年来,贝叶斯统计分析理论已逐渐被引入混凝土领域[5-6],利用其特殊的解决问题的理念进行构件或结构的相关计算,综合考虑先验信息和样本信息对先验模型进行更新,从而可得精度高、随机性小的后验模型。本文结合国内外37 组PRC 连梁抗剪试验数据,应用贝叶斯多元线性参数估计方法,构造无信息先验分布作为参数的先验分布,建立了PRC 连梁基于中国《钢骨混凝土结构技术规程》(YB9082—2006)、中国《组合结构设计规范》(JGJ138—2016)、美国规范(ACI318-02和AISC(1999))和英国规范(BS8110 和BS5950)的受剪承载力概率计算模型,并采用贝叶斯后验参数剔除过程,进行模型简化。并进行对比分析,检验模型的准确性、有效性及优越性。
1 各国规范计算模型简介
关于PRC 连梁抗剪承载力的计算,目前没有统一的计算模型和方法。本文参阅国内外相关规程,整理了中国《钢骨混凝土结构技术规程》(YB9082—2006)[7]、中国《组合结构设计规范》(JGJ138—2016)[8]、美国混凝土协会规范(ACI318-02)[9]和美国钢结构协会规范(AISC(1999))[10]、英国混凝土规范(BS8110)[11]和英国钢结构规范(BS5950)[12]中的相关计算公式,见表1。其中结合ACI318-02 和AISC(1999)分别计算混凝土和钢板的抗剪承载力贡献(Vn)RC、(Vn)s,并组合得PRC连梁的极限抗剪承载力(Vn)comp。结合BS8110 和BS5950 分别计算混凝土、箍筋和钢板的抗剪承载力贡献Vc、Vv、Vp,并组合得PRC 连梁的极限抗剪承载力Vu。
2 钢板-混凝土组合连梁的构造做法
目前PRC 连梁主要应用于超高层建筑中的筒体,混凝土的强度等级常取C50~C60,钢材牌号常取Q345,钢板厚度取16~36 mm,钢板的最小配板率取1.0%左右,最大配板率取3.8%~4.5%[13]。
PRC 连梁可以采用如图1、图2 所示的做法[13]。钢板应与墙肢内型钢暗柱焊接或螺栓连接,若墙肢内未设置型钢暗柱,钢板在墙肢中的埋置长度应满足La≥max(500 mm,hw)。为了便于剪力墙边缘构件的箍筋穿过,钢板伸入剪力墙部分可根据箍筋间距开设槽口,槽口间距c 和边缘构件箍筋间距相同,槽口宽度d 可取箍筋直径+2 mm,e取剪力墙钢筋混凝土保护层厚度,如图1所示。

图1 立面示意图Fig.1 Vertical face diagram
PRC连梁内置钢板的厚度应满足tw≥6 mm,高度宜满足hw≤0.7h。为保证钢板与混凝土共同工作,可在钢板表面焊接栓钉,栓钉直径应不小于16 mm,长度至少取4 倍栓钉直径,间距至少取6倍栓钉直径。连梁腰筋的拉结钢筋可预先在钢板上留孔穿过,或将拉结钢筋直接焊于钢板上,如图2所示。

图2 剖面示意图Fig.2 Cross-section diagram
3 试验值与规范计算值比较
本文统计了37 组PRC 连梁斜截面受剪承载力试验数据[1-4,14-15],考虑了试件截面尺寸(b、h)、内嵌钢板截面尺寸(tw、hw)、内嵌钢板屈服强度fpy、混凝土强度fcu、箍筋强度fyv、配板率ρp、纵筋配筋率ρs及箍筋配筋率ρsv等影响因素,对其进行了统一整理,见表2。由表2 可知,该37 根PRC 连梁试件截面宽度b 的范围为100~180 mm,截面高度h的范围为250~600 mm,跨高比ln∕h 的范围为0.9~2.5,钢板截面tw、hw范围分别为2~20 mm、95~540 mm,钢板配板率ρp的范围为0.84%~12.43%,混凝土抗压强度fcu的范围为37~59.9 MPa,钢板强度fpy的范围为200~280 MPa。利用表1 所列各国规范的计算模型分别对该37 根试件梁进行受剪承载力的计算,并将计算值与试验值进行对比,结果列于表2中的修正前Vtest∕Vcal处。
4 贝叶斯概率模型建立
4.1 贝叶斯无信息先验分布参数估计法
假设随机变量y 和自变量x1,x2,…,xp之间存在线性关系[16]:
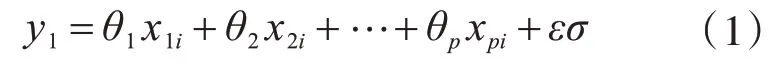
其中,各εi独立同分布于N(0,1),即εi~N(0,1)。
假设未知参数(θ,σ)的先验信息是未知的,则据贝叶斯假设可得其先验分布为


表1 钢板混凝土组合连梁斜截面受剪承载力计算模型Table 1 Shear strength calculation model for plate-reinforced composite coupling beams

表2 钢板-混凝土组合连梁抗剪试验数据概况Table 2 Database of plate-reinforced composite coupling beams shear test
据贝叶斯定理可得参数(θ,σ)的后验信息,其中θ 的后验分布为多元t 分布,据t 分布性质可求得θ 的后验期望值和协方差值。σ2的后验分布为逆Gamma分布,据逆Gamma分布的性质可求得σ2的后验期望值。
4.2 模型建立
根据贝叶斯统计理论,采用公式(3)来建立PRC 连梁斜截面受剪承载力计算的概率分析模型[17]:

式中:Θ=(θ,σ)为未知的模型参数;Vd为先验模型,本文采用表1 所列四种规范模型;γ(X,θ)为修正项,其表达式见式(4);ε表示正态随机变量,且ε~Ν(0,1);σ表示模型进行修正后仍存在的误差。
另外,假定模型方差σ2独立于影响因素X,即对于给定的X,θ和σ,模型V(X,θ)的方差是σ2,而不是X的函数。

式中,hi(x)是对影响参数的评估,见表3。
对式(3)进行对数运算,则

将式(5)转化为多元线性模型,见式(6)。
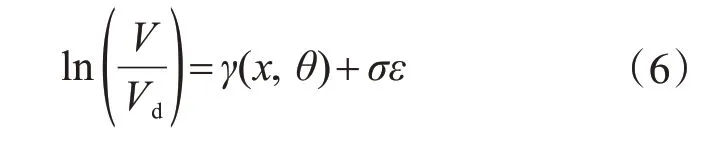
利用式(6)建立PRC 连梁受剪承载力的贝叶斯概率模型:令Vd=VYB,带入表3 中的各影响因素hi(x)项,根据4.1 节介绍的贝叶斯无信息先验分布参数估计法,对未知模型参数(θ,σ)进行估计,即可得V=VB,YB,为基于YB 9082—2006 的概率计算模型;然后分别令Vd=VJGJ、VACI、VBS,同理可得V=VB,JGJ、V=VB,ACI、V=VB,BS,分别为基于JGJ 138—2016的概率计算模型、基于ACI 318-02 和AISC(1999)的概率计算模型、基于BS5950 和BS8110 的概率计算模型。
表3 Table 3 hi(x)

表3 Table 3 hi(x)
4.3 模型简化
考虑到规范模型已对某些影响因素进行了充分考虑,现利用贝叶斯统计推断理论,进行上述所得四个概率模型的简化。式(7)为θi的变异系数表达式(coefficient of variation),

式中,μi和σi分别表示参数θi后验分布的期望值和标准差值。
若cov(θj)=max,表明Vd计算模型已充分考虑hj(x)项的贡献,或在概率计算模型中hj(x)项对PRC 连梁抗剪承载力的贡献最小,考虑将hj(x)项剔除,由剩余hi(x)构造新的修正函数γ(x,θ),并重新利用无信息先验分布参数估计法对剩余模型参数(θ,σ)进行估计;再次识别并剔除cov(θk)=max对应的hk(x)项,重复上述步骤,若此时σ的后验期望值显著增大,表明在该概率计算模型中hk(x)项对PRC 连梁的抗剪承载力贡献较大,应保留该项。
在Vd=VYB的参数剔除过程中,当剔除ln(b∕h)项时,σ2值由0.036 0 减小至0.035 2,继续剔除lnλp项,σ2值仍为0.035 2,进一步剔除ln(tw∕hw)项,σ2值显著增加至0.041 3,停止剔除,详见表4。说明在计算模型VYB中已充分考虑了连梁截面尺寸和钢板配置对PRC 连梁抗剪承载力的影响,但对钢板截面尺寸的贡献考虑不够充分,因此可将概率计算模型VB,YB中ln(b∕h)项、lnλp项予以删除,其余hi(x)项应该保留,得简化概率模型,见表8。同理进行Vd=VJGJ、Vd=VACI、Vd=VBS的参数剔除,详见表5-表7。将所得四个简化概率模型列于表8。
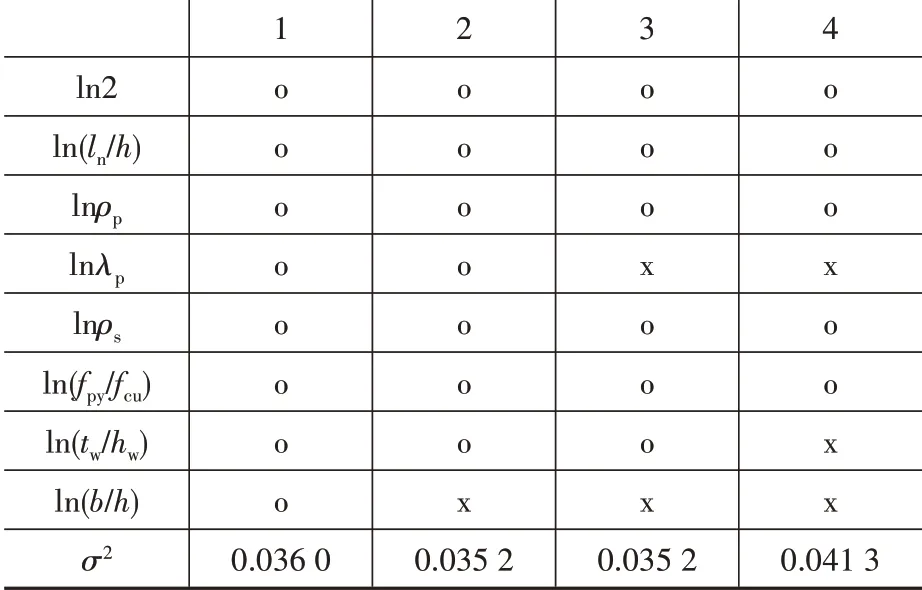
表4 基于YB 9082—2006的参数剔除过程Table 4 Stepwise deletion process based on YB 9082—2006
在表5 中,当依次剔除ln(fpy∕fcu)、ln(b∕h)、lnλp、lnρs四项时,σ2值变化不大,但再剔除ln(ln∕h)项时,σ2值由0.024 7 显著增大至0.041 0,说明在计算模型VJGJ中已充分考虑了内嵌钢板强度、混凝土强度、连梁截面尺寸、钢板配置以及纵筋配筋率对PRC 连梁抗剪承载力的影响,可以删除,但对跨高比这一因素的考虑还不够充分,应该将ln(ln∕h)项及其余hi(x)项保留在概率计算模型VB,JGJ中。
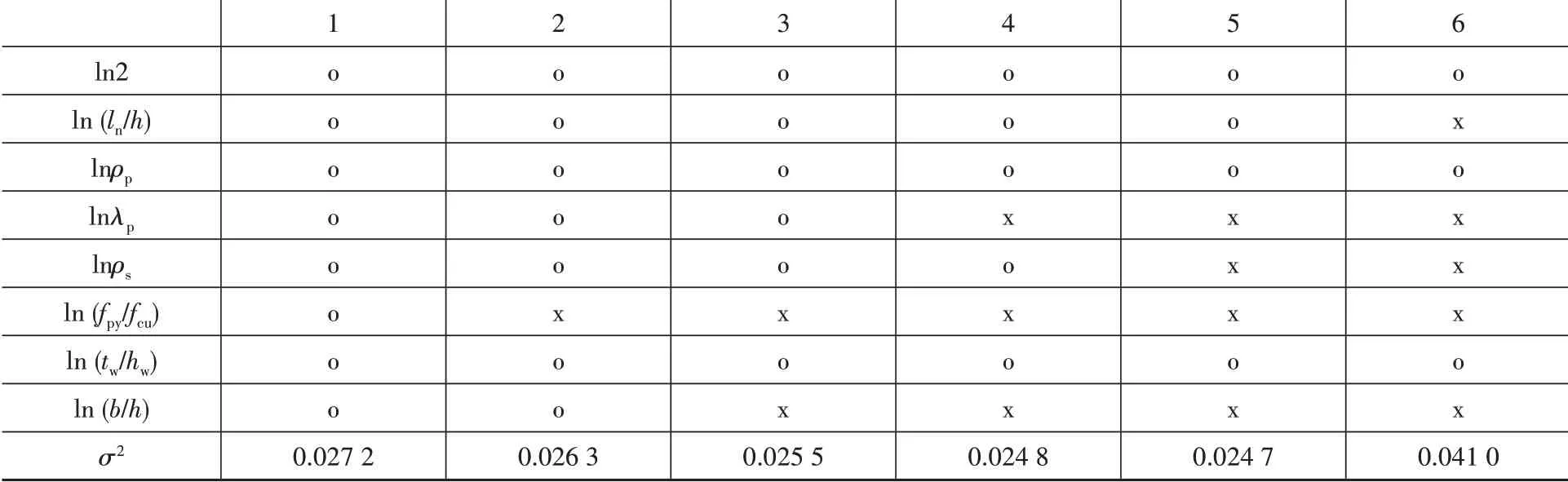
表5 基于JGJ 138—2001的参数剔除过程Table 5 Stepwise deletion process based on JGJ 138—2016
在表6 中,当依次剔除ln(b∕h)、lnλp、lnρs、ln(fpy∕fcu)四项时,σ2值变化不大,但再剔除ln(tw∕hw)项时,σ2值由0.020 8 显著增大至0.035 8,说明在VACI计算模型中已充分考虑了截面尺寸、钢板配置、纵筋配筋率、钢板强度以及混凝土强度对PRC连梁抗剪承载力的影响,可以删除,但对内嵌钢板截面尺寸这一因素的考虑还不够充分,应该将ln(tw∕hw)项及其余hi(x)项保留在概率计算模型VB,ACI中。

表6 基于ACI318-02和AISC(1999)的参数剔除过程Table 6 Stepwise deletion process based on ACI318-02 and AISC(1999)
在表7 中,当依次剔除ln(b∕h)、lnλp、lnρs、ln(fpy∕fcu)四项时,σ2值变化不大,但再剔除ln(tw∕hw)项时,σ2值由0.020 2 显著增大至0.032 6,说明在VBS计算模型中已充分考虑了连梁截面尺寸、钢板配置、纵筋配筋率、内嵌钢板强度以及混凝土强度对PRC 连梁抗剪承载力的影响,可以删除,但对内嵌钢板截面尺寸这一因素的考虑还不够充分,应该将ln(tw∕hw)项及其余hi(x)项保留在概率计算模型VB,BS中。
5 对比验证分析与讨论
利用表8 中四种概率模型进行表1 所列37 根PRC 连梁构件抗剪承载力的计算,并将计算剪力值与试验值进行对比,见表2 修正后Vtest∕Vcal处。表9 对规范计算模型与贝叶斯概率模型的计算结果进行了对比,以美国规范修正前后计算结果为例,其概率模型的均值μ(Vtest∕VB,ACI)=1.0093,较规范 模型均值μ(Vtest∕VACI)=1.1630 更接近1;且σ2(Vtest∕VB,ACI)=0.019 8,较规范模型σ2(Vtest∕VACI)=0.1033显著减小。说明利用贝叶斯概率模型进行PRC 连梁抗剪承载力计算时,计算结果更接近试验值,且随机性较小。
图3中八个小矩形位置均在1附近,但四个灰色矩形位置更接近1,尤以ACI 和BS 两组最为明显,且四个灰色矩形竖向高度偏小。进一步验证了利用贝叶斯概率模型算得的剪力值误差小一些,且离散程度小一些。图4 散点图为试验值与各计算模型计算结果比值的分布情况,结果表明,各概率计算模型所得四组样本点Vtest∕Vcal关于影响参数fcu和λp的分布,分别与对应规范计算模型所得样本点Vtest∕Vcal关于影响参数fcu和λp的分布相同,但前者较后者更集中,可见概率模型继承了规范先验模型的发展趋势,并显著降低了先验模型的偏差和随机性。

表7 基于BS5950和BS8110的参数剔除过程Table 7 Stepwise deletion process based on BS5950 and BS8110

表8 抗剪简化概率模型的均值和标准差Table 8 Mean(divided by the base model Vd(X))and coefficient of variation(c.o.v.)

表9 模型对比分析Table 9 Comparative analysis between models

图3 箱线图Fig.3 Box plot

图4 规范模型修正前后对比Fig.4 Comparative analysis of code models before and after bias-correction
6 结 论
在已有研究基础上,本文结合规范模型和试验数据,采用贝叶斯统计推断的思想,建立了PRC连梁的抗剪概率模型。根据分析结果,可以得出以下结论:
(1)在模型简化环节中,根据贝叶斯理论,可以判断不同规范模型背景下,各影响参数对PRC连梁构件抗剪承载力的影响程度,进而在不降低模型精度的前提下剔除影响程度小的修正项。四个规范计算模型对PRC 连梁的跨高比ln∕h、配板率ρp以及钢板截面尺寸tw∕hw的影响程度考虑不够充分,均需保留在概率计算模型中;另YB 9082—2006 模型对纵筋配筋率ρs考虑不够充分,也需保留。
(2)通过贝叶斯理论建立的PRC 连梁的四个概率抗剪模型降低了对应规范模型的偏差和随机性,并继承了其发展趋势,可对PRC 连梁斜截面抗剪承载力进行无偏估计。

