L形钢板仓组合剪力墙抗剪承载力模拟分析
王 轩 郁有升,2* 张海宾
0 引 言
钢板仓组合剪力墙是一种新型受力构件,如图1所示,是一种以两块钢板和圆管支撑组成的基本单元,该基本单元的两侧分别为底板和顶板,底板通过冷加工弯折成卷边槽形,在底板和顶板上焊接圆管支撑,底板的卷边与顶板焊接,空腔内填充混凝土[1]。
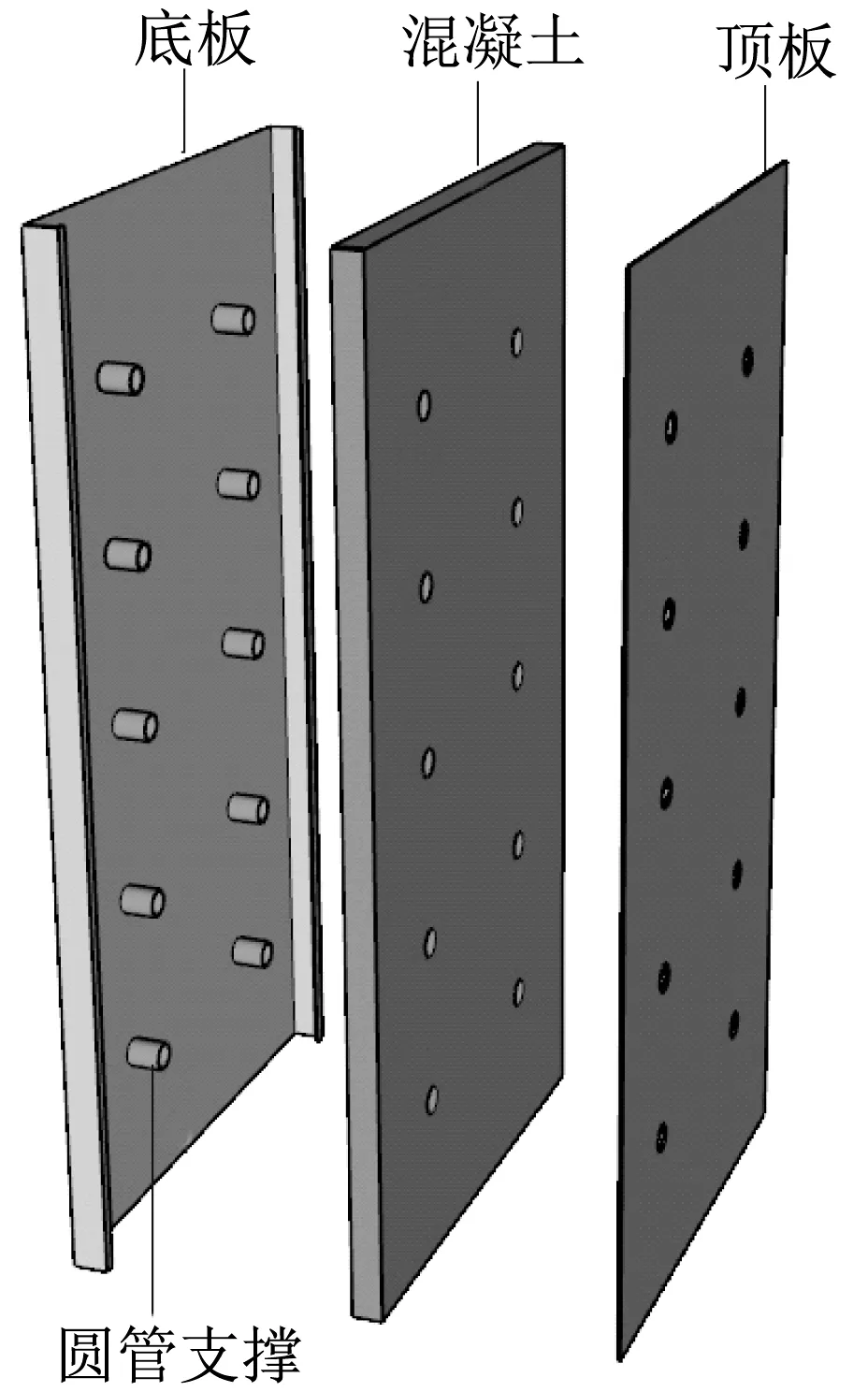
图1 钢板仓组合剪力墙示意图Fig.1 Schematic diagram of steel silo composite shear wall
钢板仓组合剪力墙中外包钢板和圆管支撑具有良好的整体性,圆管支撑能防止钢板过早地发生局部屈曲,提高钢板与混凝土协同工作的能力;钢板和圆管支撑能有效约束住内部混凝土,限制混凝土的横向变形,使混凝土三向受力,提高其承载力、塑性和韧性;内填混凝土能增强钢板的稳定性,对外包钢板提供平面外约束,从而提高了组合剪力墙的延性和变形能力;同时还具有钢板壁薄、工厂预制、构造简单、施工方便、运输方便、经济性能良好等优点。
钢板-混凝土组合剪力墙是一种承载力高、延性好、抗震能力强的新型墙体结构,国内外学者对组合剪力墙进行了一系列研究,Wright 等对双面压型钢板内填混凝土组合剪力墙在施工荷载和使用阶段荷载作用下的轴压及抗剪性能进行了研究[2]。Emori 等在双层钢板间焊接加劲肋的组合剪力墙进行试验研究[3]。石继兵等对内置钢板带高强混凝土中高剪力墙抗震性能进行了试验研究[4]。肖建庄等对钢板-高强混凝土组合剪力墙的火灾反应进行了数值模拟[5]。程春兰等对带约束拉杆的双钢板-混凝土组合剪力墙承载力和变形能力进行分析[6]。朱立猛等对研究带约束拉杆钢板混凝土组合剪力墙的抗震性能及螺栓连接的可靠性进行研究[7]。Eom 等进行了对带约束拉杆的矩形和T形截面的双层钢板混凝土组合剪力墙进行了往复加载试验研究[8]。
目前国内外关于钢板仓组合剪力墙的研究处于初始阶段,对异形截面剪力墙的研究相对滞后。因此,为了更深入研究L 形截面的钢板仓组合剪力墙的受力性能,本文基于通用有限元分析软件Abaqus 建立了22 个钢板仓组合剪力墙L 形截面的分析模型,主要研究的参数为圆管支撑布置密度、轴压比、钢板厚度、高宽比、钢材强度和腹板长度,分析并研究这6 个因素对其抗剪承载力、延性性能及变形能力的影响。
1 有限元模型的建立
1.1 试件参数
本文设立22 个L 形钢板仓组合剪力墙试件模型进行有限元分析,选取截面形式为L形截面,如图2 所示,编号为GBC1-GBC22,L 形截面剪力墙由腹板和翼缘两片墙体组合而成,沿加载方向的那片墙为腹板,而与加载方向垂直的则为翼缘。基准试件GBC-1 的钢材采用Q345B,墙翼缘b 长1 200 mm,腹板L 长1 200 mm,墙厚t 为150 mm,钢板厚度t0为4mm,墙高H 为2 400 mm,圆管支撑直径d 为50 mm,翼缘圆管支撑的间距X×Y 为400 mm×600 mm,腹板圆管支撑的间距X×Y 为400 mm×600 mm,翼缘和腹板的圆管支撑的个数为2×6(2列6行),混凝土的强度为C30,其他试件均在基准试件GBC-1基础上改变参数得出。具体的试件尺寸如表1所示。
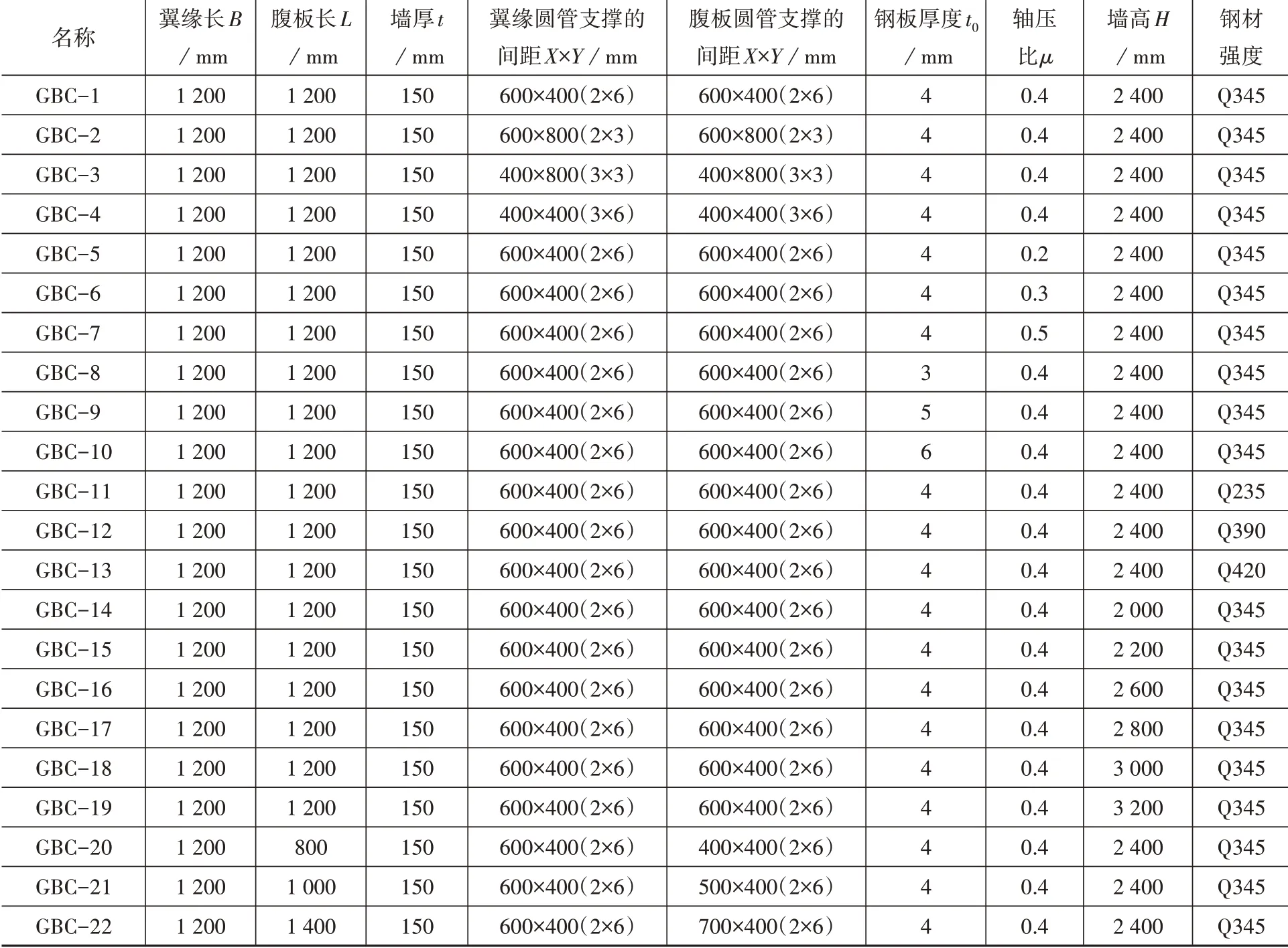
表1 L形钢板仓组合剪力墙模型参数表Table 1 Parameters table of L-shaped steel silo composite shear wall models
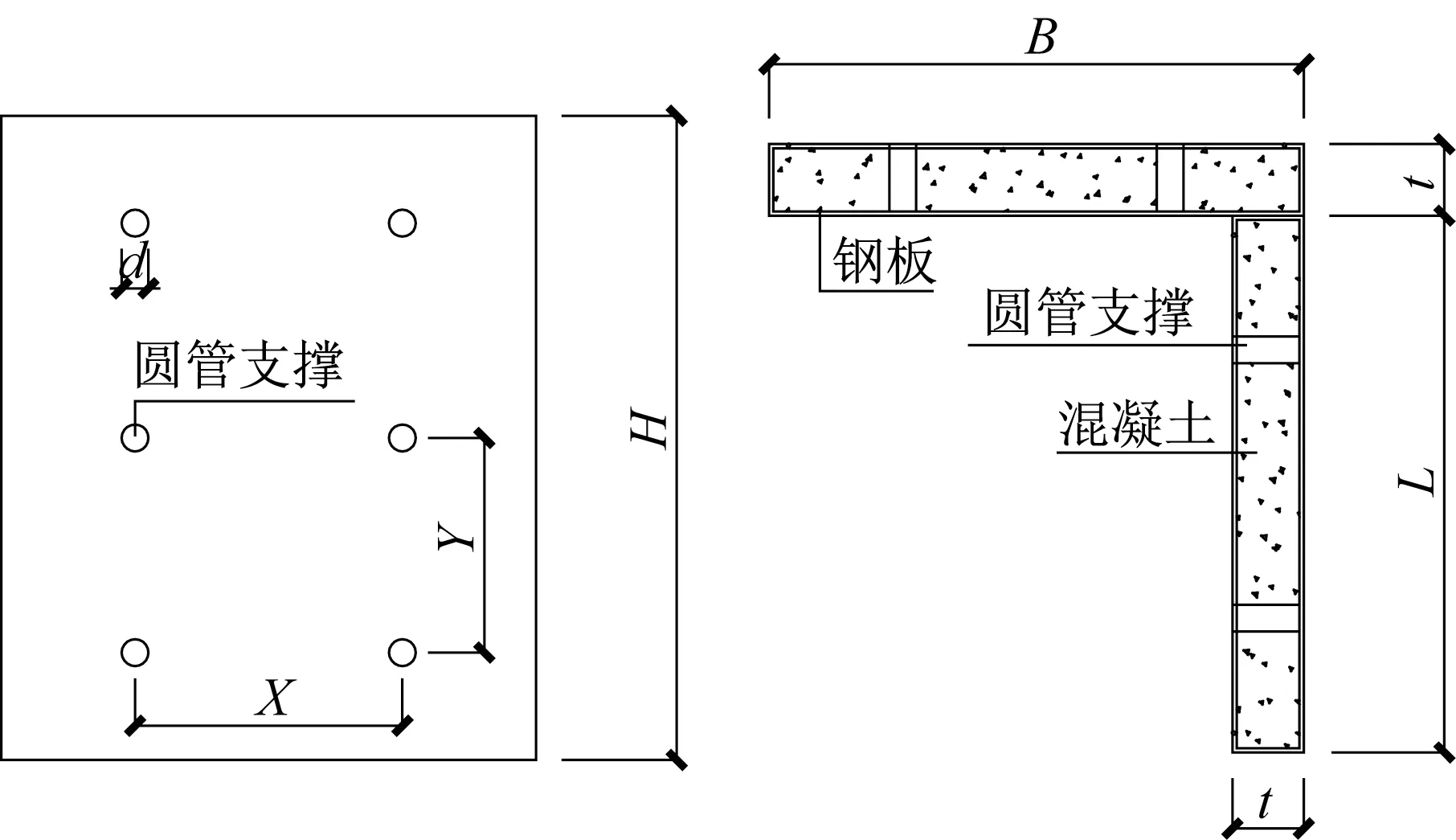
图2 L形钢板仓组合剪力墙示意图Fig.2 Schematic diagram of L-shaped steel silo composite shear wall
1.2 有限元分析模型
钢材本构模型依据Von Mises 屈服准则,钢材的单轴应力-应变关系曲线采用如图3 所示的二折线模型,钢材材料参数见表2。混凝土采用C30,在ABAQUS 有限元分析中,混凝土采用塑性损伤模型,混凝土受压应力-应变关系曲线采用韩林海约束本构[9]。

图3 钢材应力应变关系曲线Fig.3 Steel stress-strain curve

表2 钢材材料属性Table 2 Materials properties of steel MPa
为了尽可能地使有限元模型和实际情况相符合,钢板和内部填充混凝土均采用Abaqus∕Standard 建立考虑几何非线性和材料非线性的三维实体模型,钢板和混凝土的单元类型均为C3D8R。加载过程中钢板与混凝土之间采用面与面接触,切向采用罚摩擦,摩擦系数μ=0.25[10],法向接触为硬接触。钢材之间采用Tie约束连接。
模型底部全部固结以模拟基础,即底部约束住6 个位移方向。施加荷载时,首先在模型顶部施加轴向荷载,再在模型顶部耦合中心点上施加水平荷载,加载方向沿腹板受压方向加载,模型加载方式采用位移控制加载。有限元模型如图4所示。
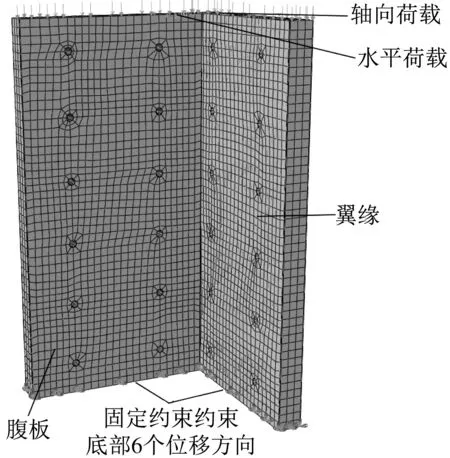
图4 有限元模型Fig.4 Finite element model
试件上的轴压力通过轴压比来控制,轴压比μ[11]计算公式如下:

式中:N 为轴压力设计值;fc为混凝土轴心抗压强度;fy为钢材的屈服强度;Ac和As分别为剪力墙墙肢内混凝土部分和钢板部分的截面面积。
1.3 模型验证
引用文献[12]中的BLC-C-1 试件数据进行模拟验证,根据上述的建模方法及本构关系建立Abaqus 有限元模型。将文献[12]提取的骨架曲线与本文模拟的骨架曲线进行对比,如图5 所示。可以看出有限元计算曲线与试验曲线的吻合较好,说明本文Abaqus 有限元模型建立方法具有可靠性。
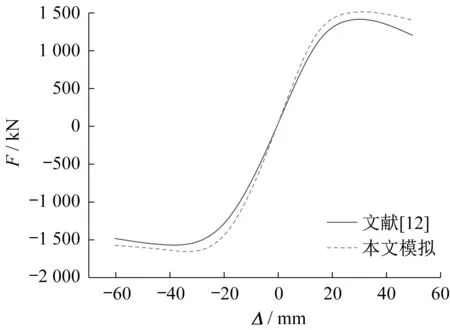
图5 试验曲线与模拟曲线对比Fig.5 Comparison of experimental and simulated curves
2 计算结果分析
2.1 破坏形态
通过有限元模拟分析表明,L 形钢板仓组合剪力墙典型破坏形态为受弯破坏。在弹性阶段内,L 形钢板仓组合剪力墙无明显的变形,圆管支撑无明显变形,外包钢板与内填混凝土共同受力、协同工作。其荷载-位移曲线呈线性增长;随着荷载的增加,组合剪力墙腹板逐渐进入到屈服阶段,剪力墙腹板无翼缘侧底部外包钢板率先达到屈服荷载,随后外包钢板出现屈曲并产生微小鼓曲,并且钢板的鼓曲现象从腹板无翼缘侧逐渐向腹板翼缘侧延展,组合剪力墙的翼缘的外包钢板却无明显变形,还在弹性阶段未达到屈服荷载。腹板底部圆管支撑,发生轻微变形,但能正常工作,翼缘圆管支撑无明显变化。其荷载-位移曲线在达到极限荷载之前,即使其腹板部分的受压钢板发生轻微鼓曲现象,组合剪力墙所承担的荷载仍在不断增加;随着荷载的继续加大,组合剪力墙腹板率先进入到破坏阶段,腹板底部钢板发生较大鼓曲,塑性变形过大,同时外包钢板和腔内混凝土部分发生分离,腔内混凝土被压碎,认为此时试件已经破坏,而剪力墙的翼缘塑性变形较小,故试件破坏时翼缘还未发生破坏。试件破坏时,腹板底部圆管支撑变形较大,与外包钢板断裂而失效,翼缘圆管支撑无明显变形正常工作。试件破坏模式如图6所示。
2.2 圆管支撑布置密度的影响
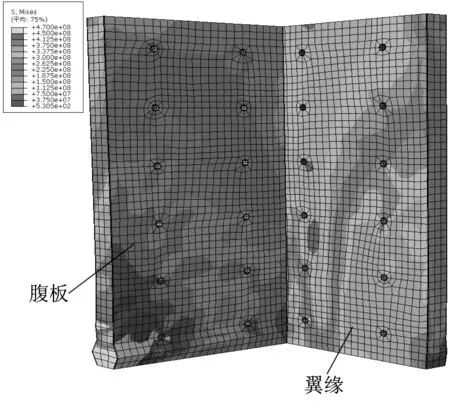
图6 试件破坏模式Mises应力云图Fig.6 Specimen failure mode Mises stress nephogram
表3 为钢板仓组合剪力墙对应的承载力特征参数。本文采用几何作图法[13]来确定模型的屈服点,极限位移取极限荷载下降到85%时所对应的位移值。延性系数的定义为剪力墙极限位移与屈服位移之比,即u=Δd∕Δy。
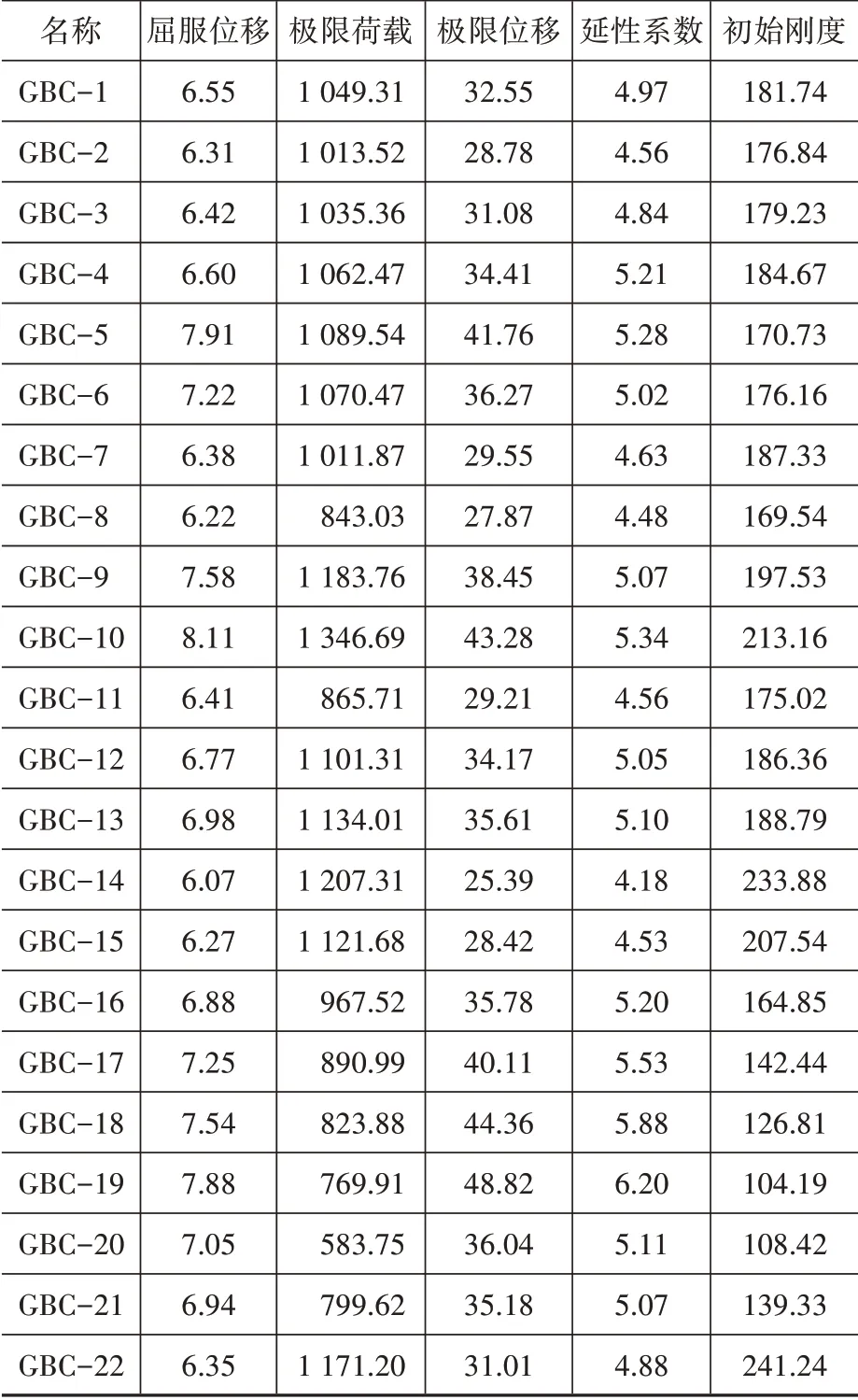
表3 L形钢板仓组合剪力墙承载力特征参数Table 3 Characteristic parameters of bearing capacity of L-shaped steel silo composite shear wall
模型GBC-1、GBC-2、GBC-3 和GBC-4 变化的参数为圆管支撑布置密度,其余参数不变。表4和图7表明,L形钢板仓组合剪力墙圆管支撑布置密度为600 mm×800 mm(2×3)、400 mm×800 mm(3×3)、600 mm×400 mm(2×6)、400 mm×400 mm(3×6)时,其 极 限 荷 载 分 别 为1 013.52kN、1 035.36 kN、1 049.31 kN、1 062.4 kN,极限位移分别为28.78 mm、31.08 mm、32.55 mm、34.41 mm,初始刚度为176.84 kN∕mm,179.23 kN∕m、181.74 kN∕mm,184.67 kN∕mm。与墙圆管支撑布置密度600 mm×800 mm(2×3)相比,墙圆管支撑布置密度增加到400 mm×800 mm(3×3)、600 mm×400 mm(2×6)、400 mm×400 mm(3×6)时,L 形钢板仓组合剪力墙的极限荷载分别提高了2.15%、3.53%、4.83%,极限位移分别增加了7.99%、13.10%、19.56%,初始刚度分别提高了1.35%、2.77%、4.43%。圆管支撑布置密度对极限荷载影响较小,但对变形能力和延性性能影响较大。圆管支撑布置密度增加,外包钢板的整体性增强,增强了钢板对混凝土的约束,防止钢板过早出现局部屈曲发生失稳导致承载力下降。L 形钢板仓组合剪力墙模型的延性系数均大于4,下降段也无突变,说明L形钢板仓组合剪力墙具有良好的延性性能和变形能力。
2.3 轴压比的影响
模型GBC-1、GBC-5、GBC-6 和GBC-7 变化的参数为轴压比,其余参数不变。表3 和图8 表明,钢板仓组合剪力墙轴压比为0.2、0.3、0.4、0.5 时,其极限荷载分别为1 089.54 kN、1 070.47 kN、1 049.31 kN、1 011.87 kN,极限位移分别为41.76 mm、36.27 mm、32.55 mm、29.55 mm,初始刚度为170.73 kN∕m、176.16 kN∕mm、181.74 kN∕mm、187.33 kN∕m。与轴压比0.2 相比,轴压比增加到0.3、0.4、0.5 时,L 形钢板仓组合剪力墙的极限荷载分别降低了1.75%、3.69%、7.13%,极限位移分别降低了13.15%、22.05%、29.24%,初始刚度分别提高了3.18%、6.45%、9.72%。随着轴压比的增大,竖向荷载的增强使外部钢板与腔内混凝土发生部分脱离,发生局部屈曲,腔内混凝土失去了原有的约束效应承载力降低,钢板仓组合剪力墙的延性性能和变形能力变差,容易发生脆性破坏,因此L形钢板仓组合剪力墙不宜在较大轴压比情况下工作。
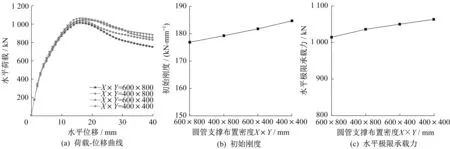
图7 圆管支撑布置密度不同时有限元分析结果Fig.7 Finite element analysis results of arrangement density of different circular supporting pipes
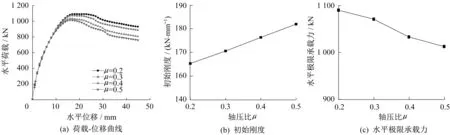
图8 轴压比不同时有限元分析结果Fig.8 Finite element analysis results of different axial compression ratio
2.4 钢板厚度的影响
模型GBC-1、GBC-8、GBC-9 和GBC-10 变化的参数为钢板厚度,其余参数不变。表3 和图9 表明,钢板仓组合剪力墙钢板厚度为3 mm、4 mm、5 mm、6 mm 时,其极限荷载分别为843.03 kN、1 049.31 kN、1 183.76 kN、1 346.69 kN,极限位移分别为27.87 mm、32.55 mm、38.45 mm、43.28 mm,初始刚度为169.54 kN∕mm、181.74 kN∕mm、197.53 kN∕mm、213.16 kN∕mm。与钢板厚度3 mm 相比,钢板厚度增加到4 mm、5 mm、6 mm 时,L 形钢板仓组合剪力墙的极限荷载分别提高了24.47%、40.42%、59.74%,极限位移分别增加了16.79%、37.96%、55.29%,初始刚度分别提升了7.20%、16.51%、25.73%。随着钢板厚度的增加,增强外包钢板对腔内混凝土的约束,增强套箍效应,防止外部钢板过早出现局部屈曲从而发生局部失稳导致其水平承载力下降。

图9 钢板厚度不同时有限元分析结果Fig.9 Finite element analysis results of different plate thickness
2.5 钢材强度的影响
模型GBC-1、GBC-11、GBC-12 和GBC-13 变化的参数为钢材强度,其余参数不变。表3 和图10表明,钢板仓组合剪力墙钢材强度选用Q235、Q345、Q390、Q420时,其极限荷载分别为865.71 kN、1 049.31 kN、1 101.31 kN、1 134.01 kN,极限位移分别为29.21 mm、32.55 mm、34.17 mm、35.61 mm,其 初 始 刚 度 为175.02 kN∕mm、181.74 kN∕mm、186.36 kN∕mm、188.79 kN∕mm。与钢材强度Q235相比,钢材强度选用Q345、Q390、Q420 时,钢板仓组合剪力墙的极限荷载分别提高了21.21%、7.21%、30.99%,极限位移分别增加了11.43%、16.98%、21.91%,初始刚度分别提高了3.84%、6.48%、7.87%。随着钢材强度的提高,外包钢板对腔内混凝土的约束能力逐渐提高,从而提高了腔内混凝土的承载能力,同时钢板与混凝土能更好的共同工作,防止钢板与混凝土过早脱离,使L形钢板仓组合剪力墙的极限荷载、变形能力和延性性能均有一定提高。
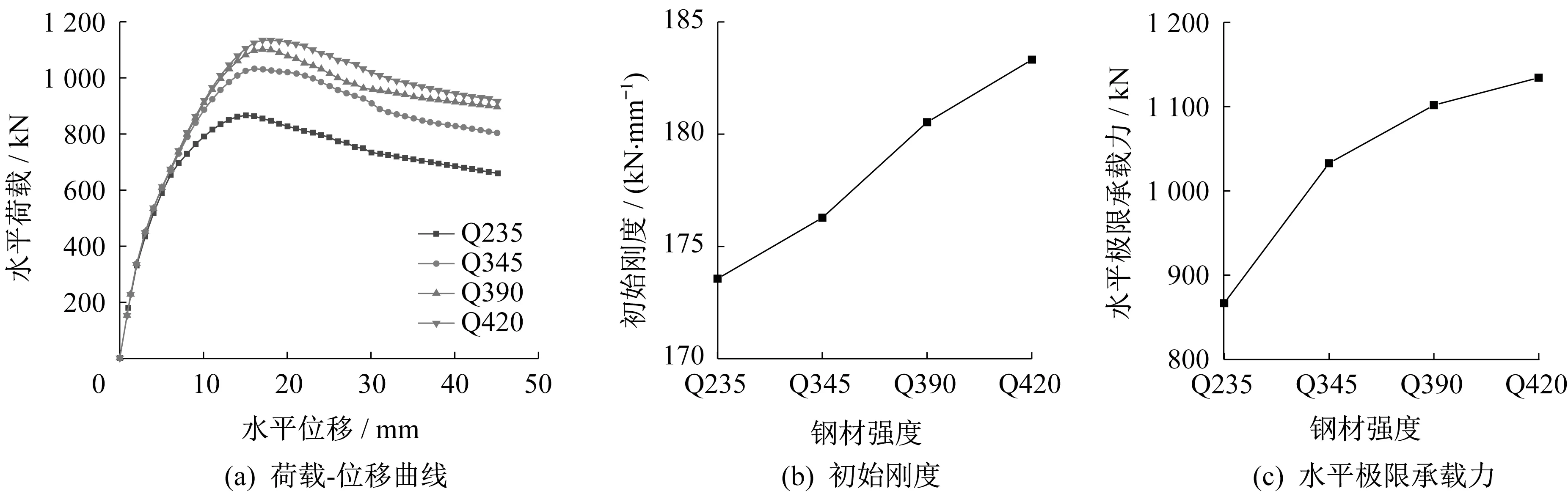
图10 钢材强度不同时有限元分析结果Fig.10 Finite element analysis results of different steel strength
2.6 高宽比的影响
模型GBC-1、GBC-14 到GBC-19 变化的参数为高宽比,其余参数不变。表3和图11表明,钢板仓组合剪力墙高宽比为1.67、1.83、2.00、2.17、2.33、2.50、2.67时,其极限荷载分别为1 207.31 kN、1 121.68 kN、1 049.31 kN、967.52 kN、890.99 kN、823.88 kN、769.91 kN,极限位移分别为25.39 mm、28.42 mm、32.55 mm、35.78 mm、40.11 mm、44.36 mm、48.82 mm,初 始 刚 度 为233.88 kN∕mm、207.54 kN∕mm、181.74 kN∕mm、164.85 kN∕mm、142.44 kN∕mm、126.81 kN∕mm、104.19 kN∕mm。与高宽比1.67 相比,高宽比增加到1.83、2.00、2.17、2.33、2.50、2.67 时,L 形钢板仓组合剪力墙的极限荷载分别降低了7.09%、13.09%、19.86%、26.20%、31.76%、36.23%,极限位移分别增加了11.93%、28.20%、40.92%、57.98%、74.71%、92.28%,初始刚度分别降低了11.26%、22.29%、29.52%、39.10%、45.78%、55.45%。随着高宽比的增大,L 形钢板仓组合剪力墙的初始刚度和极限荷载明显下降,但其延性性能提高,变形能力增强。L 形钢板仓组合剪力墙也由弯剪破坏变为弯曲破坏。高宽比是影响L形钢板仓组合剪力墙破坏形式、变形能力、延性性能和承载力的关键因素,为避免发生脆性破坏通常要求L形钢板仓组合剪力墙的高宽比不应过小。
2.7 腹板长度的影响
模型GBC-1、GBC-20、GBC-21 和GBC-22 变化的参数为腹板长度,其余参数不变。表3 和图12表明,L形钢板仓组合剪力墙腹板长度为800 mm、1 000 mm、1 200 mm、1 400 mm 时,其极限荷载分别为583.75 kN、799.62 kN、1 049.31 kN、1171.20 kN,极限位移分别为36.04 mm、35.18 mm、32.55 mm、31.01 mm,初始刚度为108.42 kN∕mm、139.33 kN∕mm、181.74 kN∕mm、241.24 kN∕mm。与腹板长度800mm 相比,腹板长度为1 000 mm、1 200 mm、1 400 mm 时,钢板仓组合剪力墙的极限荷载分别提高了36.98%、79.75%、100.63%,极限位移降低了2.39%、9.68%、13.96%,初始刚度分别提高了28.51%、67.63%、122.51%。随着腹板长度的加长,L 形钢板仓组合剪力墙的极限荷载和初始刚度大幅提高,屈服位移和极限位移呈下降的趋势,变形能力和延性性能降低。腹板是L形钢板仓组合剪力墙得到主要抗侧力构件,腹板长度对L 形钢板仓组合剪力墙的抗剪性能影响较大,翼缘为辅助受力构件,翼缘能有效约束住腹板,有效防止剪力墙发生平面外失稳和扭转破坏,翼缘对变形能力、稳定性和延性性能有较大影响。
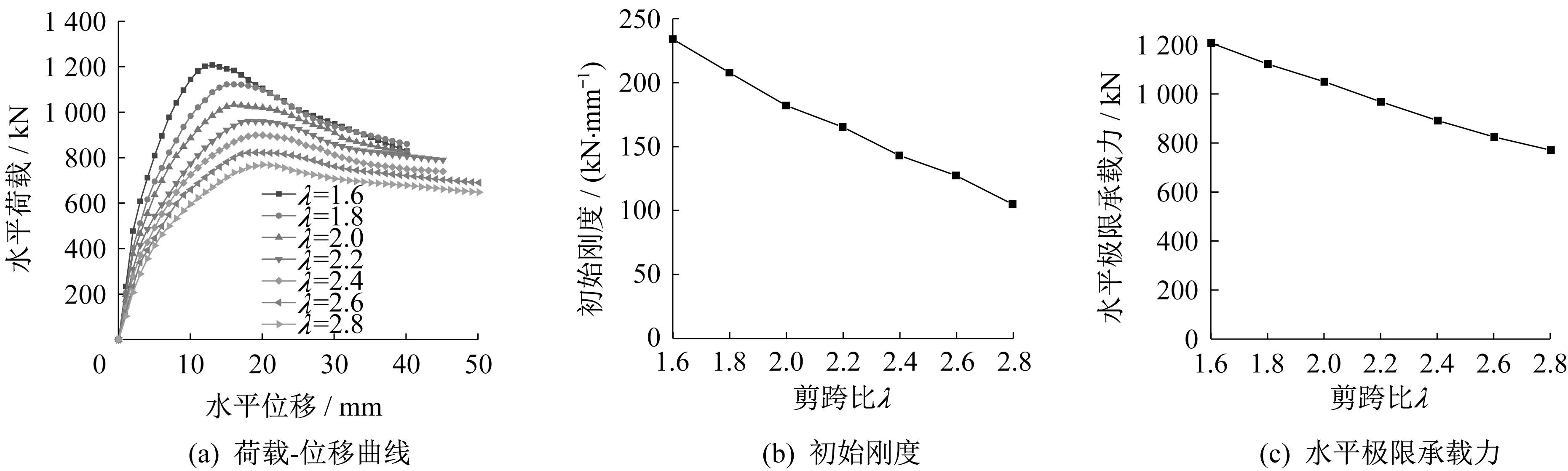
图11 高宽比不同时有限元分析结果Fig.11 Finite element analysis results of different aspect ratio

图12 腹板长度不同时有限元分析结果Fig.12 Finite element analysis results of different web length
3 L 形钢板仓组合剪力墙抗剪承载力计算
目前对于L 形钢板仓组合剪力墙,国内外对其极限承载力计算公式没有统一的规定,主要的计算方法包括叠加法和半经验半公式法等方法[14]。本文采用叠加法提出L 形钢板仓组合剪力墙试件的抗剪承载力计算公式。Abaqus 有限元分析中表明,L形钢板仓组合剪力墙的圆管支撑布置密度、轴压比、钢板厚度、高宽比、钢材强度和腹板长度这6 个因素对L形钢板仓组合剪力墙试件的抗剪承载力有影响,考虑这些因素对L形钢板仓组合剪力墙承载力所贡献的比例,考虑翼缘与腹板对试件水平承载力的综合影响,L 形钢板仓组合剪力墙腹板为主要抗侧力构件,翼缘为辅助腹板受力,推导出合适的公式。通过多项函数拟合得出公式(2)如下:
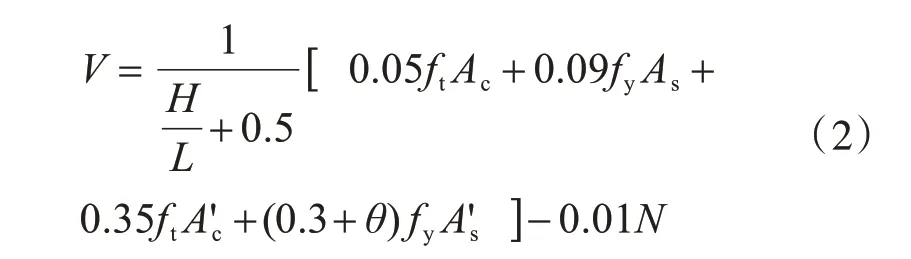
式中:V 为L 形钢板仓组合剪力墙抗剪承载力;H为墙高;L 为腹板长;ft为混凝土轴心抗拉强度;fy为钢材的屈服强度;Ac和As分别为剪力墙翼缘内混凝土部分和钢板部分的有效截面面积;A'c和A's分别为剪力墙腹板内混凝土部分和钢板部分的有效截面面积;d 为圆管支撑直径;N 为墙体承担的轴压力;θ 为圆管支撑布置间距影响系数,见式(3)。

式中:d 为圆管支撑的直径,建议其取值范围为30~80 mm;X 为腹板圆管支撑水平间距;Y 为腹板圆管支撑竖向间距。
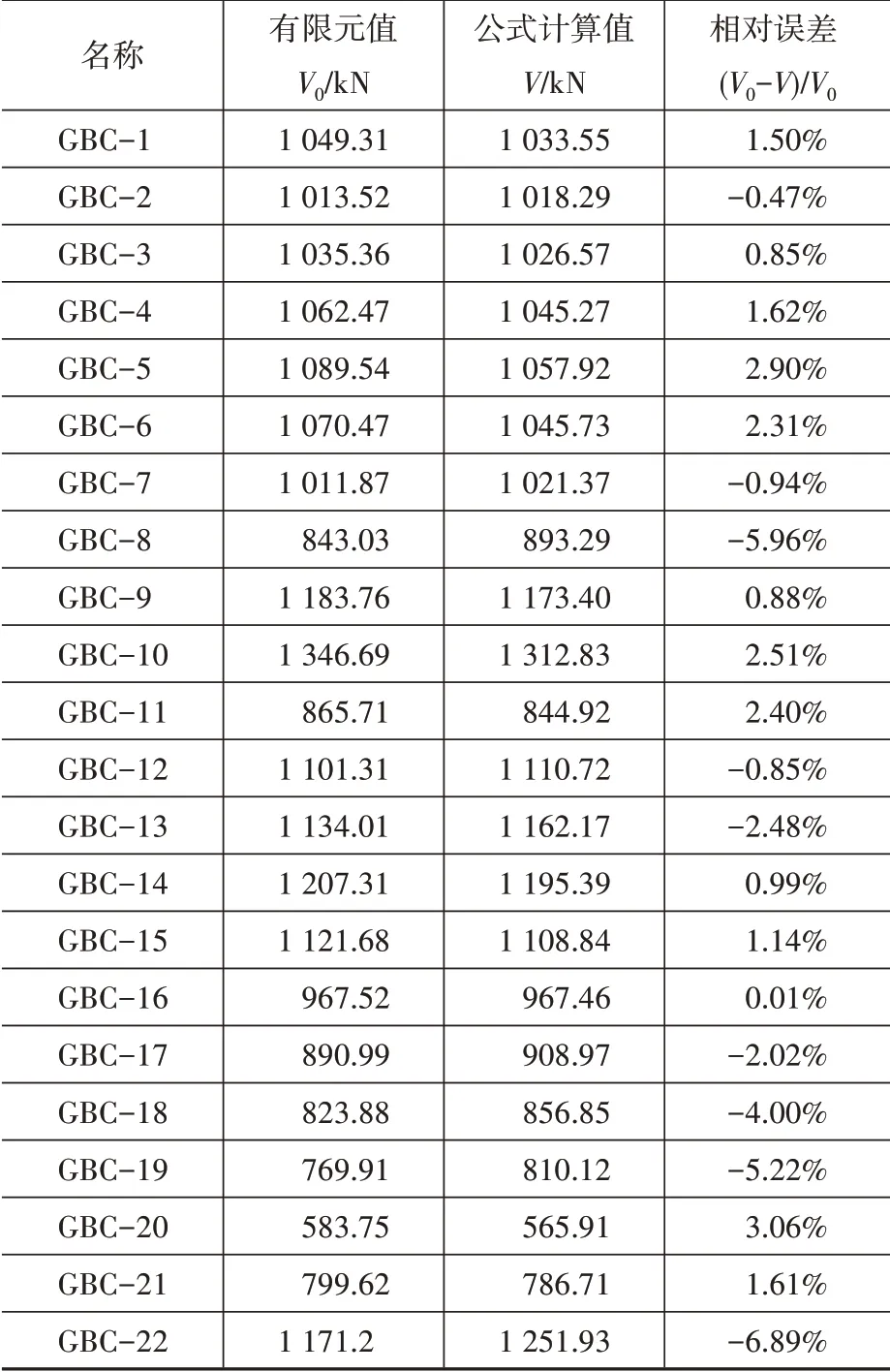
表4 抗剪承载力计算值与有限元对比Table 4 Comparisons of ultimate bearing capacity with finite element method
通过表4 对比可以得出,本文的推导公式计算值与有限元模拟值误差在±8%以内,说明推导公式具有可靠性。
4 结 论
本文利用Abaqus 有限元分析软件建立了22个钢板仓组合剪力墙L 形截面的有限元实体模型。参数化分析了圆管支撑布置密度、轴压比、钢板厚度、高宽比、钢材强度和腹板长度这6 个因素对其承载力和延性性能的影响。结果表明:
(1)L 形钢板仓组合剪力墙具有较高的抗剪承载力和良好的变形能力。腹板为L形钢板仓组合剪力墙主要抗侧力构件,翼缘辅助腹板受力,翼缘能有效约束住腹板,有效防止剪力墙发生平面外失稳和扭转破坏,翼缘对变形能力、稳定性和延性性能有较大影响。
(2)圆管支撑布置密度、钢板厚度和钢材强度的增加,L 形钢板仓组合剪力墙的极限荷载、延性性能和变形能力均提高;轴压比增大,其极限荷载、延性性能和变形能力均降低;高宽比增加,其极限荷载降低,但延性性能和变形能力提高;腹板长度的加长,其极限荷载提高,但延性性能和变形能力降低。
(3)采用叠加法并考虑了翼缘与腹板对试件抗剪承载力的综合影响,提出L形钢板仓组合剪力墙承载力公式,本文所提出的抗剪承载力公式计算,计算结果与模拟结果吻合较好,可以为设计提供依据。

