利用改进的并行粒子群算法对变分资料同化的研究

董怡琦，周明睿，刘力源，余一冬，陈 科，童亚拉，2

(1.湖北工业大学理学院，武汉 430068；2.湖北省能源光电器件与系统工程技术研究中心，武汉 430068)

自20世纪初以来，数值天气预测作为一种预测方法，受到了广泛的关注.随着高性能计算机的诞生，高分辨率数值模式MM5的使用也成为一种热门手段.Bjerknes[1]提出从数值预测整体来看，其中重要一个环节在于初始场，其数据是否精准对最终输出影响极大.MM5中的资料同化是一种变分资料同化，属于非线性优化问题.近年来，为了改进变分同化准确性和收敛性效率，粒子群算法(PSO)、遗传算法(GA)等经典群智能算法被引到资料同化中.王顺风、白晨等[2-3]分别提出了两种遗传算法(GA)同化方案，郑琴[4]从PSO着手，改变惯性权重的变换策略，选择合适的学习因子，设计了动态惯性权重粒子群算法(PSODIWAF)，该算法能有效解决含有不连续开关过程的变分资料同化问题.为满足对精度和同化时间的要求，各种改进的粒子群算法被利用到资料同化中，李成、张顶学[5-6]等对陷入局部最优的问题进行了改进；刘明、袁小平[7-8]等采用不同的学习机制，通过效率更高的迭代公式，在收敛速度上作出了改进，减少了收敛时间；何莉等[9]重点从运行时间进行突破，采用多核处理能力提高了算法处理速度，其采用的是粒子随机替换策略，为了保证整个群体能够进行信息交流，同时也设置了共享区域；郑琴[10]和张成兴[11]分别设计了动态惯性权重粒子群算法(PSODIWAF)和时变双重压缩因子粒子群算法(PSOTVCF)将其用于资料同化.尽管在收敛精度上两种算法都有了较大的改进，但同化时间仍然存在缺陷.因此，受文献[12]的启发，本文设计了一种改进的并行算法.该算法通过并行计算对粒子群完成分组，采用PSOTVCF进行深度搜索，同时将具有不连续“开关”过程的变分资料同化作为应用场景，建立了一种新的同化模型.在几乎没有降低同化精度的前提中，极大地提高了同化速度，减少了同化时间.

1 资料同化和粒子群算法简介

1.1 资料同化的模式方程

文献[4]中的偏微分方程被用作资料同化处理中的控制方程：

(1)

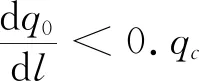
(2)

模拟参数化过程中的“on-off”开关.可将(1)式转化为其数值模式：

(3)

式中，空间格点用i表示，空间步长用Δl表示，且有li=iΔl.Δt为时间步长，tk=kΔt，k为空间层.N=T/Δt为积分过程中总的时间层；M+1=(L/Δl)+1为空间离散点总数.

1.2 粒子群算法

在PSO中，D维空间的搜索个体用粒子表示，粒子拥有位置和速度两个属性.其每个时刻所在的位置被看作是待求解问题的一个候选解，粒子位置的变换认为是最优解的寻找过程.以及其移动速度是受截止到上一时刻自身所经历过的最优位置和整个群体到达最优位置的影响，每次迭代进行相应调整.

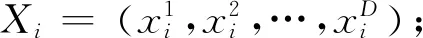
用下列公式对粒子进行操作：

(4)

(5)

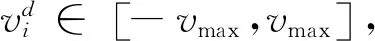
迭代终止条件没有固定的要求，通常规定为当前定位到的最优位置已经达到了设定的最小适应阈值或者达到了设定的最大迭代次数.

2 改进的并行粒子群算法

2.1 设计思路

文献[11]中设计了一种时变双重压缩因子粒子群算法(PSOTVCF)，在惯性权重的基础上引入双重压缩因子进行迭代.虽然提高了同化精度，但也因此使收敛速度变慢，同化时间增加.为解决同化时间过长的问题，本文受文献[12]的启发，将粒子群分成四个子集，分配多核CPU中一个核给每个子集进行计算，迭代的同时粒子与其他子集进行信息交流，从而每个粒子都能较好地掌握整个种群的迭代状况，并且利用PSOTVCF进行粒子的更新.

2.2 时变双重压缩因子粒子群算法的并行处理

一般地，并行问题的处理有两种方法：(1)功能分解形式，对问题自身进行拆分，将一个大问题拆分成几个子问题，然后再加以解决；(2)域分解形式，对问题区域进行分解，对分解后的区域并行处理.P2PSO中采用区域分解形式进行并行，同时引入协同进化的策略.首先根据CPU核数确定分为4组，然后在主线程中依据分组数设定4个线程，再对每个线程进行任务分配.并行中信息交流也有两种方法：同步和异步.同步形式是4个线程内粒子都完成了位置速度更新后，再评估和更新全局最优个体的位置和速度.异步形式[12]是只要有其中一个线程内完成了个体最优粒子位置速度的更新，就马上评估和更新全局最优粒子信息.P2PSO算法属于并行算法，本质上是模拟鸟群捕食行为.因鸟群捕食过程中，只要有一只鸟发现了食物，便会通过一些形式去告知其他的鸟，而不是等所有的鸟都找到食物再去通知，这就是“即时种群通信行为”.因此该算法在信息交流的并行化中采用异步形式，每个线程完成了组内粒子的更新后，申请获取读写同步锁来更新整个种群内全局最优粒子信息.

2.3 并行时变双重压缩因子粒子群算法

算法引入PSOTVCF进行深度搜索，惯性权重ω用压缩因子取代，缓解全局与局部探寻间的矛盾关系.其中通过加速因子计算得到压缩因子，加速因子的计算公式为

(6)

其中，C1N是第一个加速因子的最大值，C1M是第一个加速因子的最小值，C2N是第二个加速因子的最大值，C2M是第二个加速因子的最小值.MAXITER是设定的最大迭代数，ITER是当前迭代次数.

PSOTVCF中粒子速度更新公式表示：

v(t+1)=χ(v(t)+φy(t))，

(7)

y(t+1)=χv(t)+(1-χφ)y(t)，

(8)

由此得到系统矩阵：

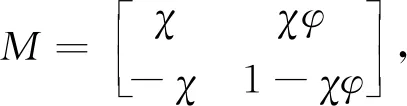
(9)

φ=C1+C2，

(10)

满足条件φ>4，由收敛准则得到压缩因子的定义：

(11)

其中，压缩因子χ为正实数，且χ∈(0，1).

单一压缩因子[13]在高维多峰函数应用中精度较低且平衡全局和局部搜索中能力极为限制，所以采用双重压缩因子.

速度计算公式转换为：

v(t+1)=χ1(v(t)+C1Rand

(Pi-x(t)+C2Rand(Pg+x(t))))，

(12-1)

v(t+2)=χ2⊗(v(t+1)).

(12-2)

χ1和χ2均由公式(10)和(11)计算，其中χ1中加速因子取得是设定的初始值，而χ2中采用的是时变的加速因子，先由公式(6)计算加速因子再代入公式(10)(11)中.

设循环次数为N，得到最终简化的粒子速度：

V(N)=(χ2⊗χ1)N-1(V(0)+φY).

(13)

时变双重压缩因子粒子群算法有效地改进了粒子群算法容易陷入局部最优的问题.

在变分资料同化应用过程中，其中代价函数通过该公式进行计算：

(14)

其中

(15)

表示q0满足物理约束和相容性条件，这里q为q0代入模式方程(1)的解.

式(14)离散化后得到离散化函数：

(16)

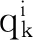
PSOTVCF算法中采用的适应度函数是：

(17)

其中

(18)

P2PSO的算法流程如下：

1)对算法参数进行初始化，设定整个群体粒子数P，惯性权重ω，加速因子，分组数C以及在各个分组中的最大迭代次数I.

2)读写同步锁设定，按照设定的分组数依次建立线程，在各个线程中确定组内粒子数Pi和终止条件最大迭代次数I.

5)分组线程申请获取读写同步锁.

6)将更新后的组内最优解pgi与此时整个种群的最优解pg进行比较，若pgi优于pg，则令pg=pgi.

7)分组线程释放读写同步锁.

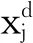
9) 判断是否满足迭代终止条件，如果组内迭代数达到预先设置的最大迭代数I，则停止该线程的计算，若不满足则转为步骤(4).

10)直至所有线程迭代结束，产生结果.

3 数值实验结果分析

3.1 仿真环境

采取文献[11]的实验数据和实验分析方法，将三种算法——PSOTVCF、PSODIWAF和P2PSO分别应用于变分资料同化，在精度和时间上进行比较.其中，在P2PSO中，惯性权重ω从0.7线性递减到0.1，C1N=2.98，C1M=2.78，C2N=1.55，C2M=1.35，种群中含有200个粒子，设定迭代最大次数为200，测试环境为硬件Intel Core i5，软件MATLAB R2017a.

3.2 收敛精度

图1表示的是在迭代200次时，三种算法在200次同化实验后的平均收敛精度图.图中，自上而下的横线分别表示PSODIWAF，P2PSO，PSOTVCF，纵坐标是收敛精度的对数log10J，其值越小表示同化质量越好，同化结果越准确.从实验结果可直观看出与PSODIWAF相比，P2PSO和PSOTVCF在同化实验结果中更为准确.两者平均收敛精度相近，但P2PSO略差与PSOTVCF.为了明确三种算法在运行过程中的差距缘由，需要继续对收敛趋势进行分析.

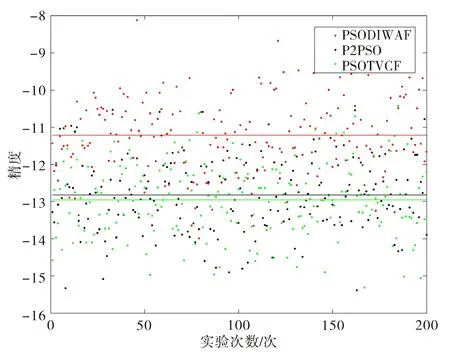
图1 三种算法在200次同化实验中平均收敛精度图Fig.1 Average convergence accuracy of three algorithms in 200 assimilation experiments

图2表示的是PSODIWAF、PSOTVCF、P2PSO在迭代200次时收敛精度的变化趋势.图中横坐标代表迭代次数，纵坐标同图1含义相同，即为收敛精度的对数log10J.星号标出的点分别为迭代次数50，100，150，200.折线从终点来看自上而下分别表示PSODIWAF，P2PSO，PSOTVCF.分段分析，在同化初期(迭代次数为50)，PSOTVCF与P2PSO结果大致相同，收敛精度均略低于PSODIWAF；同化中期(迭代次数为100)，三者同化质量相似；同化后期(迭代次数为150)，PSOTVCF和P2PSO后来居上，同化质量最好，PSODIWAF次之，并且粒子基本已经收敛；实验终点(迭代次数为200)，PSOTVCF同化质量最好，其次是P2PSO，最后是PSODIWAF，其收敛数值依次为-13、-12.9、-11.2.从整体来看，P2PSO与原算法PSOTVCF在同化初期基本保持一致，自同化中期开始，两者产生细微差距.因此P2PSO同化结果的质量高于动态权重粒子群算法，与PSOTVCF相似.并行算法的精度略低于原算法的原因，应该是由于在并行过程中信息交流的程度没有单线程的高，从而导致收敛精度降低.

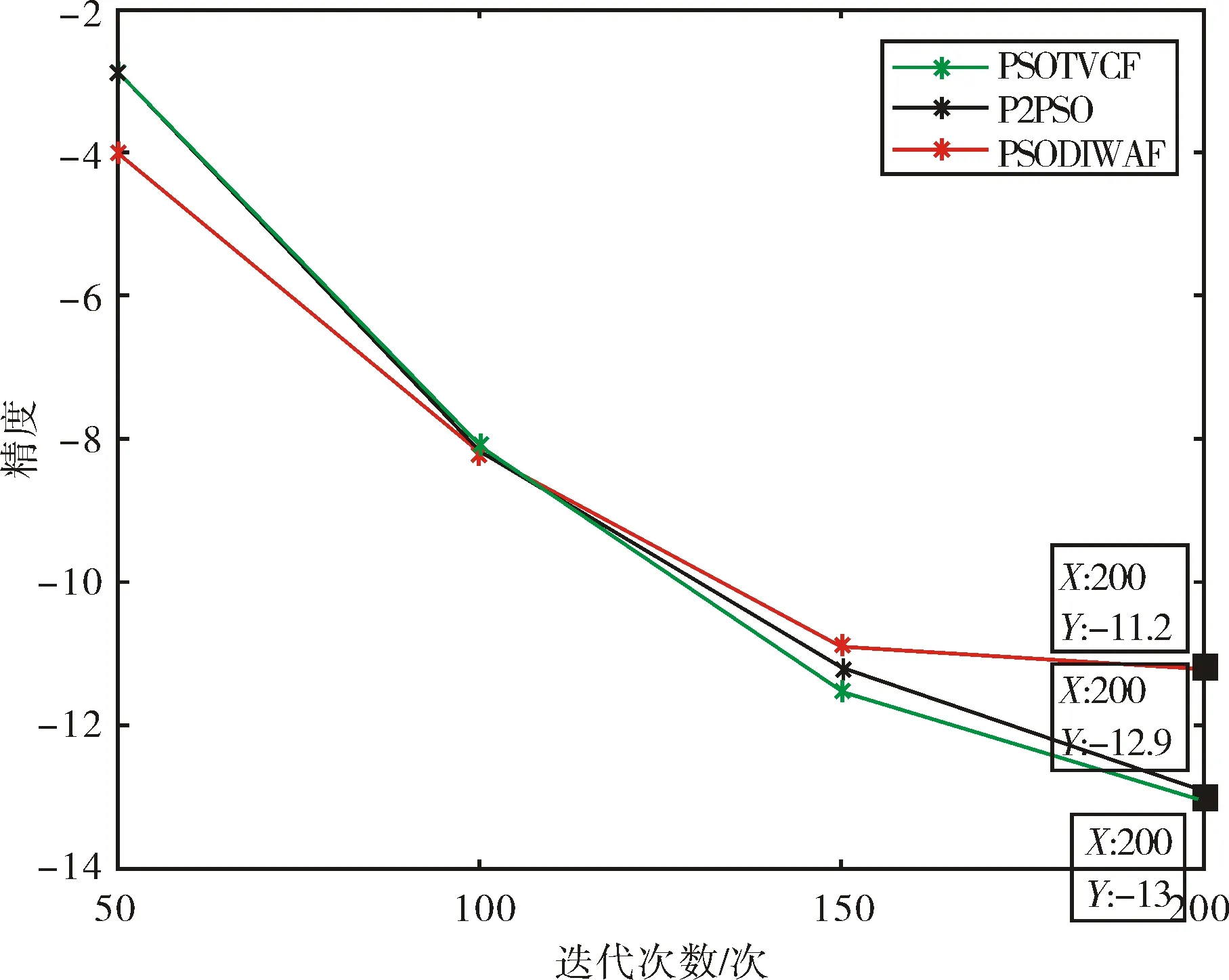
图2 三种算法收敛精度变化趋势对比图Fig.2 Comparison of convergence accuracy trends of three algorithms

3.3 同化时间

将PSOTVCF、PSODIWAF和P2PSO应用于资料同化问题中，同时记录三种算法在迭代次数为50，100，150，200时所花费的时间.因为粒子群算法具有一定的随机性，为了使数据更加有说服力，每一个同化窗口进行6组实验.将6组试验数据平均值记录于表1中.

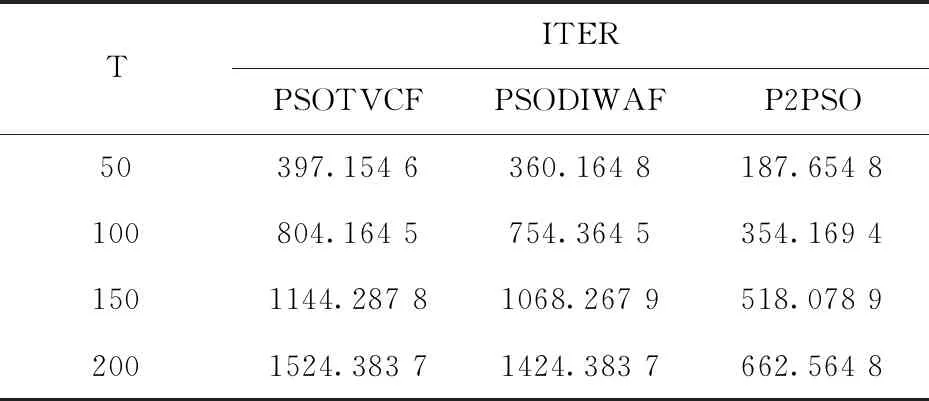
表1 三种算法在迭代次数为50，100，150，200时平均同化时间(s)对比表Tab.1 Comparison of average assimilation time(seconds) of three algorithms with iteration times of 50,100,150,200 s

通过表中数据，直观上可得到无论迭代次数是在50，100，150还是200，P2PSO的同化速度都要比PSOTVCF和PSODIWAF快，同化时间缩短一半左右.P2PSO迭代200次的时间比PSOTVCF和PSODIWAF迭代100次的时间还要短.数据上计算得出在200代迭代之后P2PSO的收敛速度和PSODIWAF相比提高了51.5%左右，和PSOTVCF相比提高了55.1%左右.因此，本文所设计的并行粒子群算法通过多个CPU的联合计算对于提高同化速度，缩短同化时间具有显著的效果.

4 结论与展望

本文着重在时间上改进了粒子群算法，结合计算机CPU的多核处理硬件知识，在不过度影响精度的情况下较大程度上加快了速度.在变分资料同化中采用所设计的算法，减少了同化时间，与时变双重压缩因子PSO和动态权重PSO算法相比在收敛速度上有了较大的提升，但在收敛精度上仍需改进.因此后续可针对因多线程导致粒子间信息交流程度略有降低的现象，对算法进一步改进，实现较大程度加快同化速度的同时也能够进一步提高收敛精度.本文将含“开关”过程的变分资料同化作为该算法的应用场景，后续可尝试着将P2PSO应用于其他场景下的资料同化，扩大所设计算法的适用空间.