关于Euler函数φ(n)的一个四元变系数混合方程的解
张四保
(喀什大学数学与统计学院,新疆 喀什 844008)
Euler函数φ(n)是数论中一个重要的函数[1-2],其性质在数论中占有非常重要的地位.包含Euler函数φ(n)的方程的研究内容众多,文献[3-6]讨论了形如φ(x1x2…xn)=k1φ(x1)+k2φ(x2)+…+knφ(xn)的线性方程整数解问题;文献[7-10]讨论了形如φ(x1x2…xn)=k1φ(x1)+k2φ(x2)+…+knφ(xn)+b的非线性方程整数解问题.文献[11]给出了三元变系数混合型方程φ(abc)=2φ(a)φ(b)+6φ(c)的全部95组正整数解;文献[12]给出了混合型方程φ(abc)=2φ(a)φ(b)+8φ(c)的全部95组正整数解.本文将讨论关于Euler函数φ(n)的一个四元变系数混合方程
φ(xyzw)=3φ(x)φ(y)+5φ(z)φ(w)
(1)
的正整数解,利用Euler函数φ(n)的计算公式以及初等方法给出了其一切正整数解.
1 定理及其证明
定理1方程(1)共有372组正整数解,并且其满足x≤y,z≤w的93组正整数解如下:(x,y,z,w)=(1,7,1,19),(1,7,1,27),(1,7,1,38),(1,7,1,54),(1,7,2,19),(1,7,2,27),(1,9,1,19),(1,9,1,38),(1,9,2,19),(1,14,1,19),(1,14,1,27),(1,18,1,19),(2,7,1,19),(2,7,1,27),(2,9,1,19),(1,15,1,16),(1,16,1,15),(3,5,1,16),(1,16,3,5),(1,11,1,7),(1,11,1,9),(1,11,1,14),(1,11,1,18),(1,11,2,7),(1,11,2,9),(1,22,1,7),(1,22,1,9),(2,11,1,7),(2,11,1,9),(1,25,1,8),(1,25,1,12),(1,33,1,5),(1,33,1,8),(1,33,1,10),(1,33,2,5),(1,44,1,5),(1,66,1,5),(2,33,1,5),(1,25,3,4),(3,11,1,5),(3,11,1,8),(3,11,1,10),(3,11,2,5),(3,22,1,5),(4,11,1,5),(1,5,2,8),(1,5,2,12),(1,8,1,8),(1,8,1,10),(1,8,1,12),(1,8,2,5),(1,10,1,8),(1,10,1,12),(1,12,1,8),(1,12,1,10),(1,12,2,5),(2,5,1,8),(2,5,1,12),(2,8,1,5),(2,12,1,5),(1,5,4,4),(1,5,4,6),(1,8,3,4),(1,10,3,4),(2,5,3,4),(3,4,1,8),(3,4,1,10),(3,4,2,5),(4,4,1,5),(4,6,1,5),(1,11,2,4),(1,11,2,6),(1,22,1,4),(1,22,1,6),(1,22,2,3),(2,11,1,4),(2,11,1,6),(2,11,2,3),(2,22,1,3),(1,3,2,18),(1,6,1,18),(1,6,2,9),(2,3,1,18),(2,3,2,9),(2,6,1,9),(1,4,2,4),(1,4,2,6),(1,6,2,4),(2,3,2,4),(2,4,1,4),(2,4,1,6),(2,4,2,3),(2,6,1,4).
证明由于n≥φ(n),则有
3φ(x)φ(y)+5φ(z)φ(w))≤
8φ(x)φ(y)φ(z)φ(w),
进而有
F(x,y,z,w)=
说明由于当n≥3时,有φ(n)为偶数,因而下文在讨论的过程中,若φ(x)φ(y)或φ(z)φ(w)为大于1的奇数的情况都不予考虑.
情况1当F(x,y,z,w)=1时.
此时,有(xy,zw)=1,(x,y)=(z,w)=1,由方程(1)有φ(x)φ(y)φ(z)φ(w)=3φ(x)φ(y)+5φ(z)φ(w),则有
因而有φ(x)φ(y)=6,φ(z)φ(w)=18;φ(x)φ(y)=8,φ(z)φ(w)=8;φ(x)φ(y)=10,φ(z)φ(w)=6;φ(x)φ(y)=20,φ(z)φ(w)=4.
情况1.1当φ(x)φ(y)=6,φ(z)φ(w)=18时,有φ(x)=1,φ(y)=6,φ(z)=1,φ(w)=18;φ(x)=1,φ(y)=6,φ(z)=18,φ(w)=1;φ(x)=6,φ(y)=1,φ(z)=1,φ(w)=18;φ(x)=6,φ(y)=1,φ(z)=18,φ(w)=1.
当φ(x)=1,φ(y)=6,φ(z)=1,φ(w)=18,此时有x=1,2,y=7,9,14,18,z=1,2,w=19,27,38,54,此时方程(1)有解(x,y,z,w)=(1,7,1,19),(1,7,1,27),(1,7,1,38),(1,7,1,54),(1,7,2,19),(1,7,2,27),(1,9,1,19),(1,9,1,38),(1,9,2,19),(1,14,1,19),(1,14,1,27),(1,18,1,19),(2,7,1,19),(2,7,1,27),(2,9,1,19).
在方程(1)中,x与y具有对称性,z与w具有对称性,由对称性可知当φ(x)=1,φ(y)=6,φ(z)=18,φ(w)=1时,方程(1)有解(x,y,z,w)=(1,7,19,1),(1,7,27,1),(1,7,38,1),(1,7,54,1),(1,7,19,2),(1,7,27,2),(1,9,19,1),(1,9,38,1),(1,9,19,2),(1,14,19,1),(1,14,27,1),(1,18,19,1),(2,7,19,1),(2,7,27,1),(2,9,19,1);当φ(x)=6,φ(y)=1,φ(z)=1,φ(w)=18时,方程(1)有解(x,y,z,w)=(7,1,1,19),(7,1,1,27),(7,1,1,38),(7,1,1,54),(7,1,2,19),(7,1,2,27),(9,1,1,19),(9,1,1,38),(9,1,2,19),(14,1,1,19),(14,1,1,27),(18,1,1,19),(7,2,1,19),(7,2,1,27),(9,2,1,19);当φ(x)=6,φ(y)=1,φ(z)=18,φ(w)=1时,方程(1)有解(x,y,z,w)=(7,1,19,1),(7,1,27,1),(7,1,38,1),(7,1,54,1),(7,1,19,2),(7,1,27,2),(9,1,19,1),(9,1,38,1),(9,1,19,2),(14,1,19,1),(14,1,27,1),(18,1,19,1),(7,2,19,1),(7,2,27,1),(9,2,19,1).
情况1.2当φ(x)φ(y)=8,φ(z)φ(w)=8时,有φ(x)=1,φ(y)=8,φ(z)=1,φ(w)=8;φ(x)=1,φ(y)=8,φ(z)=8,φ(w)=1;φ(x)=8,φ(y)=1,φ(z)=1,φ(w)=8;φ(x)=8,φ(y)=1,φ(z)=8,φ(w)=1;φ(x)=2,φ(y)=4,φ(z)=1,φ(w)=8;φ(x)=2,φ(y)=4,φ(z)=8,φ(w)=1;φ(x)=4,φ(y)=2,φ(z)=1,φ(w)=8;φ(x)=4,φ(y)=2,φ(z)=8,φ(w)=1;φ(x)=1,φ(y)=8,φ(z)=2,φ(w)=4;φ(x)=1,φ(y)=8,φ(z)=4,φ(w)=2;φ(x)=8,φ(y)=1,φ(z)=2,φ(w)=4;φ(x)=8,φ(y)=1,φ(z)=4,φ(w)=2;φ(x)=2,φ(y)=4,φ(z)=2,φ(w)=4;φ(x)=2,φ(y)=4,φ(z)=4,φ(w)=2;φ(x)=4,φ(y)=2,φ(z)=2,φ(w)=4;φ(x)=4,φ(y)=2,φ(z)=4,φ(w)=2.
当φ(x)=1,φ(y)=8,φ(z)=1,φ(w)=8时,有x=1,2,y=w=15,16,20,24,30,z=1,2,此时方程(1)有解(x,y,z,w)=(1,15,1,16),(1,16,1,15).由对称性可得当φ(x)=1,φ(y)=8,φ(z)=8,φ(w)=1时,方程(1)有解(x,y,z,w)=(1,15,16,1),(1,16,15,1);当φ(x)=8,φ(y)=1,φ(z)=1,φ(w)=8时,方程(1)有解(x,y,z,w)=(15,1,1,16),(16,1,1,15);当φ(x)=8,φ(y)=1,φ(z)=8,φ(w)=1时,方程(1)有解(x,y,z,w)=(15,1,16,1),(16,1,15,1).
当φ(x)=2,φ(y)=4,φ(z)=1,φ(w)=8时,有x=3,4,6,y=5,8,10,12,z=1,2,w=15,16,20,24,30,此时方程(1)有解(x,y,z,w)=(3,5,1,16).由对称性可得当φ(x)=2,φ(y)=4,φ(z)=8,φ(w)=1时,方程(1)有解(x,y,z,w)=(3,5,16,1);当φ(x)=4,φ(y)=2,φ(z)=1,φ(w)=8时,方程(1)有解(x,y,z,w)=(5,3,1,16);当φ(x)=4,φ(y)=2,φ(z)=8,φ(w)=1时,方程(1)有解(x,y,z,w)=(5,3,16,1).
当φ(x)=1,φ(y)=8,φ(z)=2,φ(w)=4时,有x=1,2,y=15,16,20,24,30,z=3,4,6,w=5,8,10,12,此时方程(1)有解(x,y,z,w)=(1,16,3,5).由对称性可得当φ(x)=1,φ(y)=8,φ(z)=4,φ(w)=2时,方程(1)有解(x,y,z,w)=(1,16,5,3);当φ(x)=8,φ(y)=1,φ(z)=2,φ(w)=4时,方程(1)有解(x,y,z,w)=(16,1,3,5);当φ(x)=8,φ(y)=1,φ(z)=4,φ(w)=2时,方程(1)有解(x,y,z,w)=(16,1,5,3);
当φ(x)=2,φ(y)=4,φ(z)=2,φ(w)=4时,有x=z=3,4,6,y=w=5,8,10,12,此时方程(1)无正整数解.由对称性可得当φ(x)=2,φ(y)=4,φ(z)=4,φ(w)=2与φ(x)=4,φ(y)=2,φ(z)=2,φ(w)=4与φ(x)=4,φ(y)=2,φ(z)=4,φ(w)=2时,方程(1)无正整数解.
情况1.3当φ(x)φ(y)=10,φ(z)φ(w)=6时,有φ(x)=1,φ(y)=10,φ(z)=1,φ(w)=6;φ(x)=1,φ(y)=10,φ(z)=6,φ(w)=1;φ(x)=10,φ(y)=1,φ(z)=1,φ(w)=6;φ(x)=10,φ(y)=1,φ(z)=6,φ(w)=1.
当φ(x)=1,φ(y)=10,φ(z)=1,φ(w)=6时,有x=1,2,y=11,22,z=1,2,w=7,9,14,18,此时方程(1)有解(x,y,z,w)=(1,11,1,7),(1,11,1,9),(1,11,1,14),(1,11,1,18),(1,11,2,7),(1,11,2,9),(1,22,1,7),(1,22,1,9),(2,11,1,7),(2,11,1,9).由对称性可得当φ(x)=1,φ(y)=10,φ(z)=6,φ(w)=1时,方程(1)有解(x,y,z,w)=(1,11,7,1),(1,11,9,1),(1,11,14,1),(1,11,18,1),(1,11,7,2),(1,11,9,2),(1,22,7,1),(1,22,9,1),(2,11,7,1),(2,11,9,1);当φ(x)=10,φ(y)=1,φ(z)=1,φ(w)=6时,方程(1)有解(x,y,z,w)=(11,1,1,7),(11,1,1,9),(11,1,1,14),(11,1,1,18),(11,1,2,7),(11,1,2,9),(22,1,1,7),(22,1,1,9),(11,2,1,7),(11,2,1,9);当φ(x)=10,φ(y)=1,φ(z)=6,φ(w)=1时,方程(1)有解(x,y,z,w)=(11,1,7,1),(11,1,9,1),(11,1,14,1),(11,1,18,1),(11,1,7,2),(11,1,9,2),(22,1,7,1),(22,1,9,1),(11,2,7,1),(11,2,9,1).
情况1.4当φ(x)φ(y)=20,φ(z)φ(w)=4时,有φ(x)=1,φ(y)=20,φ(z)=1,φ(w)=4;φ(x)=1,φ(y)=20,φ(z)=4,φ(w)=1;φ(x)=20,φ(y)=1,φ(z)=1,φ(w)=4;φ(x)=20,φ(y)=1,φ(z)=4,φ(w)=1;φ(x)=1,φ(y)=20,φ(z)=2,φ(w)=2;φ(x)=20,φ(y)=1,φ(z)=2,φ(w)=2;φ(x)=2,φ(y)=10,φ(z)=1,φ(w)=4;φ(x)=2,φ(y)=10,φ(z)=4,φ(w)=1;φ(x)=10,φ(y)=2,φ(z)=1,φ(w)=4;φ(x)=10,φ(y)=2,φ(z)=4,φ(w)=1;φ(x)=2,φ(y)=10,φ(z)=2,φ(w)=2;φ(x)=10,φ(y)=2,φ(z)=2,φ(w)=2.
当φ(x)=1,φ(y)=20,φ(z)=1,φ(w)=4时,有x=1,2,y=25,33,44,50,66,z=1,2,w=5,8,10,12,此时方程(1)有解(x,y,z,w)=(1,25,1,8),(1,25,1,12),(1,33,1,5),(1,33,1,8),(1,33,1,10),(1,33,2,5),(1,44,1,5),(1,66,1,5),(2,33,1,5).由对称性可得当φ(x)=1,φ(y)=20,φ(z)=4,φ(w)=1时,方程(1)有解(x,y,z,w)=(1,25,8,1),(1,25,12,1),(1,33,5,1),(1,33,8,1),(1,33,10,1),(1,33,5,2),(1,44,5,1),(1,66,5,1),(2,33,5,1);当φ(x)=20,φ(y)=1,φ(z)=1,φ(w)=4时,方程(1)有解(x,y,z,w)=(25,1,1,8),(25,1,1,12),(33,1,1,5),(33,1,1,8),(33,1,1,10),(33,1,2,5),(44,1,1,5),(66,1,1,5),(33,2,1,5);当φ(x)=20,φ(y)=1,φ(z)=4,φ(w)=1时,方程(1)有解(x,y,z,w)=(25,1,8,1),(25,1,12,1),(33,1,5,1),(33,1,8,1),(33,1,10,1),(33,1,5,2),(44,1,5,1),(66,1,5,1),(33,2,5,1).
当φ(x)=1,φ(y)=20,φ(z)=2,φ(w)=2时,有x=1,2,y=25,33,44,50,66,z=w=3,4,6,此时方程(1)有解(x,y,z,w)=(1,25,3,4),(1,25,4,3).由对称性可得当φ(x)=20,φ(y)=1,φ(z)=2,φ(w)=2时,方程(1)有解(x,y,z,w)=(25,1,3,4),(25,1,4,3).
当φ(x)=2,φ(y)=10,φ(z)=1,φ(w)=4时,有x=3,4,6,y=11,22,z=1,2,w=5,8,10,12,此时方程(1)有解(x,y,z,w)=(3,11,1,5),(3,11,1,8),(3,11,1,10),(3,11,2,5),(3,22,1,5),(4,11,1,5),(6,11,1,5).由对称性可得当φ(x)=2,φ(y)=10,φ(z)=4,φ(w)=1时,方程(1)有解(x,y,z,w)=(3,11,5,1),(3,11,8,1),(3,11,10,1),(3,11,5,2),(3,22,5,1),(4,11,5,1),(6,11,5,1);当φ(x)=10,φ(y)=2,φ(z)=1,φ(w)=4时,方程(1)有解(x,y,z,w)=(11,3,1,5),(11,3,1,8),(11,3,1,10),(11,3,2,5),(22,3,1,5),(11,4,1,5),(11,6,1,5);当φ(x)=10,φ(y)=2,φ(z)=4,φ(w)=1时,方程(1)有解(x,y,z,w)=(11,3,5,1),(11,3,8,1),(11,3,10,1),(11,3,5,2),(22,3,5,1),(11,4,5,1),(11,6,5,1).
当φ(x)=2,φ(y)=10,φ(z)=2,φ(w)=2时,有x=z=w=3,4,6,y=11,22,此时方程(1)无正整数解解.由对称性可得当φ(x)=10,φ(y)=2,φ(z)=2,φ(w)=2时,方程(1)无正整数解.
情况2当F(x,y,z,w)=2时.

情况2.1当φ(x)φ(y)=4,φ(z)φ(w)=4时,有φ(x)=1,φ(y)=4,φ(z)=1,φ(w)=4;φ(x)=1,φ(y)=4,φ(z)=4,φ(w)=1;φ(x)=4,φ(y)=1,φ(z)=1,φ(w)=4;φ(x)=4,φ(y)=1,φ(z)=4,φ(w)=1;φ(x)=1,φ(y)=4,φ(z)=2,φ(w)=2;φ(x)=4,φ(y)=1,φ(z)=2,φ(w)=2;φ(x)=2,φ(y)=2,φ(z)=1,φ(w)=4;φ(x)=2,φ(y)=2,φ(z)=4,φ(w)=1;φ(x)=2,φ(y)=2,φ(z)=2,φ(w)=2.
当φ(x)=1,φ(y)=4,φ(z)=1,φ(w)=4时,有x=z=1,2,y=w=5,8,10,12,此时方程(1)有解(x,y,z,w)=(1,5,2,8),(1,5,2,12),(1,8,1,8),(1,8,1,10),(1,8,1,12),(1,8,2,5),(1,10,1,8),(1,10,1,12),(1,12,1,8),(1,12,1,10),(1,12,2,5),(2,5,1,8),(2,5,1,12),(2,8,1,5),(2,12,1,5).由对称性可得当φ(x)=1,φ(y)=4,φ(z)=4,φ(w)=1时,方程(1)有解(x,y,z,w)=(1,5,8,2),(1,5,12,2),(1,8,8,1),(1,8,10,1),(1,8,12,1),(1,8,5,2),(1,10,8,1),(1,10,12,1),(1,12,8,1),(1,12,10,1),(1,12,5,2),(2,5,8,1),(2,5,12,1),(2,8,5,1),(2,12,5,1);当φ(x)=4,φ(y)=1,φ(z)=1,φ(w)=4时,方程(1)有解(x,y,z,w)=(5,1,2,8),(5,1,2,12),(8,1,1,8),(8,1,1,10),(8,1,1,12),(8,1,2,5),(10,1,1,8),(10,1,1,12),(12,1,1,8),(12,1,1,10),(12,1,2,5),(5,2,1,8),(5,2,1,12),(8,2,1,5),(12,2,1,5);当φ(x)=4,φ(y)=1,φ(z)=4,φ(w)=1时,方程(1)有解(x,y,z,w)=(5,1,8,2),(5,1,12,2),(8,1,8,1),(8,1,10,1),(8,1,12,1),(8,1,5,2),(10,1,8,1),(10,1,12,1),(12,1,8,1),(12,1,10,1),(12,1,5,2),(5,2,8,1),(5,2,12,1),(8,2,5,1),(12,2,5,1).
当φ(x)=1,φ(y)=4,φ(z)=2,φ(w)=2时,有x=1,2,y=5,8,10,12,z=w=3,4,6,此时方程(1)有解(x,y,z,w)=(1,5,4,4),(1,5,4,6),(1,5,6,4),(1,8,3,4),(1,8,4,3),(1,10,3,4),(1,10,4,3),(2,5,3,4),(2,5,4,3).由对称性可得当φ(x)=4,φ(y)=1,φ(z)=2,φ(w)=2时,方程(1)有解(x,y,z,w)=(5,1,4,4),(5,1,4,6),(5,1,6,4),(8,1,3,4),(8,1,4,3),(10,1,3,4),(10,1,4,3),(5,2,3,4),(5,2,4,3).
当φ(x)=2,φ(y)=2,φ(z)=1,φ(w)=4时,有x=y=3,4,6,z=1,2,w=5,8,10,12,此时方程(1)有解(x,y,z,w)=(3,4,1,8),(3,4,1,10),(3,4,2,5),(4,3,1,8),(4,3,1,10),(4,3,2,5),(4,4,1,5),(4,6,1,5),(6,4,1,5).由对称性可得当φ(x)=2,φ(y)=2,φ(z)=4,φ(w)=1时,方程(1)有解(x,y,z,w)=(3,4,8,1),(3,4,10,1),(3,4,5,2),(4,3,8,1),(4,3,10,1),(4,3,5,2),(4,4,5,1),(4,6,5,1),(6,4,5,1).
当φ(x)=2,φ(y)=2,φ(z)=2,φ(w)=2时,有x=y=z=w=3,4,6,此时方程(1)无解.
情况2.2当φ(x)φ(y)=10,φ(z)φ(w)=2时,有φ(x)=1,φ(y)=10,φ(z)=1,φ(w)=2;φ(x)=1,φ(y)=10,φ(z)=2,φ(w)=1;φ(x)=10,φ(y)=1,φ(z)=1,φ(w)=2;φ(x)=10,φ(y)=1,φ(z)=2,φ(w)=1.
当φ(x)=1,φ(y)=10,φ(z)=1,φ(w)=2时,有x=z=1,2,y=11,22,w=3,4,6,此时方程(1)有解(x,y,z,w)=(1,11,2,4),(1,11,2,6),(1,22,1,4),(1,22,1,6),(1,22,2,3),(2,11,1,4),(2,11,1,6),(2,11,2,3),(2,22,1,3).由对称性可得当φ(x)=1,φ(y)=10,φ(z)=2,φ(w)=1时,方程(1)有解(x,y,z,w)=(1,11,4,2),(1,11,6,2),(1,22,4,1),(1,22,6,1),(1,22,3,2),(2,11,4,1),(2,11,6,1),(2,11,3,2),(2,22,3,1);当φ(x)=10,φ(y)=1,φ(z)=1,φ(w)=2时,方程(1)有解(x,y,z,w)=(11,1,2,4),(11,1,2,6),(22,1,1,4),(22,1,1,6),(22,1,2,3),(11,2,1,4),(11,2,1,6),(11,2,2,3),(22,2,1,3);当φ(x)=10,φ(y)=1,φ(z)=2,φ(w)=1时,方程(1)有解(x,y,z,w)=(11,1,4,2),(11,1,6,2),(22,1,4,1),(22,1,6,1),(22,1,3,2),(11,2,4,1),(11,2,6,1),(11,2,3,2),(22,2,3,1).
情况3当F(x,y,z,w)=3时.
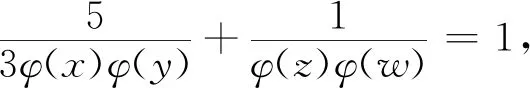
当φ(x)=1,φ(y)=2,φ(z)=1,φ(w)=6时,有x=z=1,2,y=3,4,6,w=7,9,14,18,此时方程(1)有解(x,y,z,w)=(1,3,2,18),(1,6,1,18),(1,6,2,9),(2,3,1,18),(2,3,2,9),(2,6,1,9).由对称性可得当φ(x)=1,φ(y)=2,φ(z)=6,φ(w)=1时,方程(1)有解(x,y,z,w)=(1,3,18,2),(1,6,18,1),(1,6,9,2),(2,3,18,1),(2,3,9,2),(2,6,9,1);当φ(x)=2,φ(y)=1,φ(z)=1,φ(w)=6时,方程(1)有解(x,y,z,w)=(3,1,2,18),(6,1,1,18),(6,1,2,9),(3,2,1,18),(3,2,2,9),(6,2,1,9);当φ(x)=2,φ(y)=1,φ(z)=6,φ(w)=1时,方程(1)有解(x,y,z,w)=(3,1,18,2),(6,1,18,1),(6,1,9,2),(3,2,18,1),(3,2,9,2),(6,2,9,1).
情况4当F(x,y,z,w)=4时.

当φ(x)=1,φ(y)=2,φ(z)=1,φ(w)=2时,有x=z=1,2,y=w=3,4,6,此时方程(1)有解(x,y,z,w)=(1,4,2,4),(1,4,2,6),(1,6,2,4),(2,3,2,4),(2,4,1,4),(2,4,1,6),(2,4,2,3),(2,6,1,4).由对称性可得当φ(x)=1,φ(y)=2,φ(z)=2,φ(w)=1时,方程(1)有解(x,y,z,w)=(1,4,4,2),(1,4,6,2),(1,6,4,2),(2,3,4,2),(2,4,4,1),(2,4,6,1),(2,4,3,2),(2,6,4,1);当φ(x)=2,φ(y)=1,φ(z)=1,φ(w)=2时,方程(1)有解(x,y,z,w)=(4,1,2,4),(4,1,2,6),(6,1,2,4),(3,2,2,4),(4,2,1,4),(4,2,1,6),(4,2,2,3),(6,2,1,4);当φ(x)=2,φ(y)=1,φ(z)=2,φ(w)=1时,方程(1)有解(x,y,z,w)=(4,1,4,2),(4,1,6,2),(6,1,4,2),(3,2,4,2),(4,2,4,1),(4,2,6,1),(4,2,3,2),(6,2,4,1).
情况5当F(x,y,z,w)=5时.

情况6当F(x,y,z,w)=6时.

情况7当F(x,y,z,w)=7时.

情况8当F(x,y,z,w)=8时.
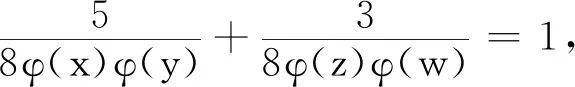
综合以上所有讨论的情况,可得定理1.证毕.
2 结语
本文讨论了形如
φ(x1x2…xn)=k1φ(x1)φ(x2)…krφ(xr)+
k2φ(xr+1)φ(xr+2)…φ(xn)
的变系数方程的一个具体的四元变系数方程φ(xyzw)=3φ(x)φ(y)+5φ(z)φ(w)的正整数解,得到了该方程有372组正整数解.对于形如
φ(x1x2…xn)=k1φ(x1)φ(x2)…krφ(xr)+
k2φ(xr+1)φ(xr+2)…φ(xn)
的方程,当n,k1,k2,r为某一组正整数时,其所确定的方程亦可采用本文的讨论方式进行讨论求解.

