高阶非线性分数阶微分方程解的存在性和唯一性

韩 伟，原战琴

(中北大学理学院，太原 030051)

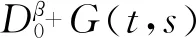
本文所研究的问题是

(1)

①f:[0，1]×[-e*，+∞)×[0，+∞)→(-∞，+∞);e*=max{e(t):t∈[0，1]};

②g:[0，1]×[-e*，+∞)×[-e*，+∞)→(-∞，+∞);且f，g都是连续函数．

(2)

1 预备知识

定义1[11]设A:Ph，e×Ph，e→E是一个混合算子，A(x，y)关于x单调递增，关于y单调递减.其中ui，vi∈Ph，e(i=1，2)，u1≤u2，v1≥v2可得A(u1，v1)≤A(u2，v2).若元素x∈Ph，e是A的一个不动点，则有A(x，x)=x．

引理1[12]设P是E中的一个正规锥，算子A，B:Ph，e×Ph，e→E是两个混合算子.满足以下条件：

1) 对于∀t∈(0，1)，∀x，y∈Ph，e，∃φ(t)∈(t，1)使得

A(tx+(t-1)e，t-1y+(t-1-1)e)≥

φ(t)A(x，y)+(φ(t)-1)e.

2) 对于∀t∈(0，1)，∀x，y∈Ph，e有

B(tx+(t-1)e，t-1y+(t-1-1)e)≥

tB(x，y)+(t-1)e.

3)A(h，h)∈Ph，e且B(h，h)∈Ph，e.

4) 存在常数δ>0，∀x，y∈Ph，e，有A(x，y)≥δB(x，y)+(δ-1)e．

则算子方程x=A(x,x)+B(x,x)+e在Ph，e上有唯一解x*，对于任给的初值x0，y0∈Ph，e有以下的序列

xn=A(xn-1，yn-1)+B(xn-1，yn-1)+e，
yn=A(yn-1，xn-1)+B(yn-1，xn-1)+e.

n=1，2，3…

则在空间E中有xn→x*，yn→x*(n→∞)成立．

引理2[9]设ζ是一个连续函数，u∈C[0，1]是分数阶微分方程边值问题(3)的一个解，

(3)

0≤s≤min{t，ξ} <1，

0<ξ≤s≤t≤1，

0≤t≤s≤ξ<1，

0≤max{t，ξ} ≤s≤1，

d=1-bξα-ν-1>0，G(t，s)作为(3)的格林函数在[0，1]×[0，1]上连续．

引理3[9]函数G(t，s)是如上引理2中所定义，则其满足如下性质：

①G(t，s)>0，∀(t，s)∈(0，1)×(0，1).

②对于∀(t，s)∈[0，1]×[0，1]有

引理4在引理3中所定义的G(t，s)有以下性质:

t，s∈[0，1]，

(4)

t，s∈[0，1].

(5)

证明首先不等式(4)已证，现在需要用(4)来证不等式(5).有

其中，d=1-bξα-ν-1>0.

从而

显然可得

综上所述，

0≤tα-β-1(1-s)α-ν-1(1-d(1+(1-s)ν-β))≤
dΓ(α-β)G(t，s)≤tα-β-1(1-s)α-ν-1，

t，s∈[0，1].

引理5[13]令α>-1，ν>0，t>0，则

有关于分数微积分的更多细节请参考文献[13]．

2 主要结论

定理1假设

①f:[0，1]×[-e*，+∞)×[0，+∞)→(-∞，+∞);e*=max{e(t):t∈[0，1]};g:[0，1]×[-e*，+∞)×[-e*，+∞)→(-∞，+∞).它们都是连续函数．

② 当t∈(0，1)时，f(t，x，y)关于第二变元x单调递增，关于第三变元y单调减.g(t，x，y)关于第二变元x单调递增，关于第三变元y单调递减．

③对于∀t∈(0，1)，∃φ(λ) ∈(λ，1)，有

f(t，λx+(λ-1)e，λ-1y+(λ-1-1)e)≥

φ(λ)f(t，x，y);

g(t，λx+(λ-1)e，λ-1y+(λ-1-1)e)≥
λg(t，x，y).

则有以下结论.

1) 存在u0，v0∈Ph，e和一个足够小的r∈(0，1)使得：rv0u0v0．有

rv0(t)≤u0(t)≤v0(t)，

其中，h(t)=Htα-1，t∈[0，1]．

2)算子方程x=A(x，x)+B(x，x)+e有一个非平凡解u*，u*∈Ph，e．

3)对任意初始值w0，τ0∈Ph，e，构造迭代序列{wn}，{τn}，其极限值为x*，wn→x*，τn→x*(n→∞),有

wn(t)=

证明∀t∈(0，1)有

因为e∈P，t∈[0，1]，所以有

Htα-1=h(t) .

因此θ≤e(t)≤h(t)使得

Ph，e={u∈C[0，1]，u+e∈Ph}.

由引理2和问题(1)积分可得

g(s，u(s)，u(s))-c)ds=

e(t)+e(t).

对∀u，v∈Ph，e，t∈ [0，1]，需考虑以下算子,

A(u，v)(t)=

所以u(t)是问题(1)的解当且仅当u=A(u，u)+B(u，u)+e．

首先，需要证明算子A，B:Ph，e×Ph，e→E是一个混合单调算子，取ui，vi∈Ph，e(i=1，2)，u1≤u2，v1≥v2.由条件②及G(t，s)>0可得

A(u1，v1)(t)=

A(u2，v2)(t)，

因此A(u1，v1)(t)≻A(u2，v2)(t)，同理B(u1，v1)(t)≻B(u2，v2)(t)．

其次，由条件③，∀λ∈(0，1)和t∈(0，1)，∃φ(t)∈(t，1)使得u，v∈Ph，e，就可得

φ(t)e(t)-φ(t)e(t)=

(φ(t)-1)e(t)=

φ(t)A(u，v)(t)+(φ(t)-1)e(t).

B(λu+(λ-1)e，λ-1v+(λ-1-1)e)(t)=

(λ-1-1)e)ds-e(t)≥

接下来证明A(u，u) ∈Ph，e，B(u，u) ∈Ph，e.只需证A(u，u)+e∈Ph，B(u，u)+e∈Ph.即可根据引理3和条件①，③得

A(h，h)(t)+e(t)=

根据条件②，④和α>β，Γ(α)>0可得

f(s，H，0)≥f(s，0，H)≥δg(s，0，H)，

s∈[0，1].

设

f(s，0，H)ds.

L2h(t)≤A(h，h)(t)+e(t)≤L1h(t)，

t∈[0，1]．

B(h，h)(t)+e(t)=

B(h，h)(t)+e(t)=

g(s，0，H)ds·tα-1=

g(s，0，H)ds·h(t).

设

g(s，0，H)ds．

同理可得L3≥L4>0,则L4h(t)≤B(h，h)(t)+e(t)≤L3h(t)，t∈[0，1]．

另一方面由条件①，②和引理3可推出

f(s，0，H)ds·tα-β-1.

g(s，h(s)，h(s))ds≤

g(s，Hsα-1，Hsα-1)ds·tα-β-1≥

g(s，0，H)ds·tα-β-1.

其中，

(1-s)ν-β))f(s，0，H)ds，

(1-s)ν-β))g(s，0，H)ds.

由条件②，④可得b1≥b2≥δb4>0，b3≥b4>0,因此A(u，u)+e∈Ph，B(u，u)+e∈Ph，对任意u，v∈Ph，e，t∈[0，1]，根据条件④可得

A(u，v)(t)=

δe(t)-δe(t)=

(δ-1)e(t)=δB(u，v)(t)+(δ-1)e(t).

则满足引理1的条件，从而定理1得证．

3 举例论证

作为应用，给出以下例子来说明主要结论．

1)考虑以下分数阶微分方程

则有

f(t，λx(t)+(λ-1)e(t)，

λ-1y(t)+(λ-1-1)e(t))=

φ(λ)f(t，x(t)，y(t)).

g(t，λx(t)+(λ-1)e(t)，λ-1y(t)+

λg(t，x(t)，y(t)).

满足条件③,将上述边界条件代入可得

可得

e(t)=

因为

则满足定理1的条件①，②，其中

是连续函数，并且关于第二变量单调递增，关于第三变量单调递减.显然

f(t，x(t)，y(t))=

g(t，x(t)，y(t)).