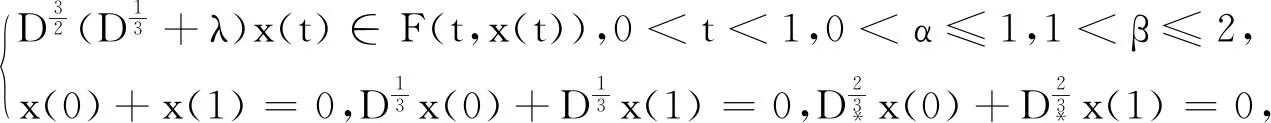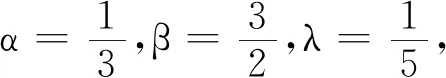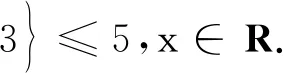带有反周期边值条件的分数阶Langevin微分包含解的存在性
杨丹丹
(淮阴师范学院数学与统计学院,江苏 淮安 223300)
2018年,文献[1]研究了如下带有反周期边值条件的分数阶Langevin微分方程:

(1)
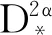
(2)
利用偏序度量空间中的混合单调映射的不动点定理,作者给出了解的存在和唯一性结果.
受文献[1]的启发,本文研究如下带有反周期边值条件的Langevin分数阶微分包含:

(3)
其中,Dα是α-阶Caputo分数阶导数,F:[0,1]×X→P(X)是一个多值映射,λ是一个实数.D2α是持续分数阶导数在文献[2]里的定义.
分数阶微分方程和微分包含,比整数阶微分方程和微分包含更能确切地描述现实世界中模型的状态,尤其是其更具有良好的记忆性和遗传性,近年来备受研究者关注[3-6].近期,关于Langevin分数阶微分方程和微分包含的研究结果,见文献[7-11].本文目的是将文献[1]中的单值结果,推广到多值情形.据笔者所知,问题(3)尚未被研究过.
1 预备知识
假设读者熟知分数阶微积分[4,12]和多值映射理论[13-14].
定义1[12]函数u:(0,∞)→R,α-分数阶Caputo导数定义为
n=[α]+1,假设等式右侧在(0,∞)上逐点有定义.
对于赋范空间(X,‖·‖),引进如下记号:
Ρcp(X)={Y∈Ρ(X):Y是紧的},
Ρcp,c(X)={Y∈Ρ(X):Y是紧凸的}.
定义2对于每个y∈C([0,T],R)y∈C([0,1],R),定义F的选择集合为SF,y∶={v∈L1([0,T],·):v(t)∈F(t,y(t))a.e.t∈[0,T]}.
定义3令(X,d)是由赋范空间(X,‖·‖)引进的度量空间.考虑Hd:Ρ(X)×Ρ(X)→R∪{∞}定义如下:
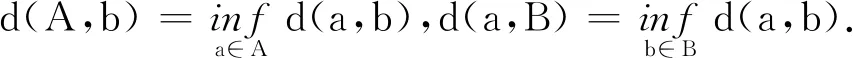
引理1[1]x(t)是问题(1)的一个解,当且仅当它是非线性混合Fredholm-Volterra积分方程的一个解:
引理2[13]令(X,d)是完备的度量空间.若N:→Pcl(X)是一个压缩映射,则FixN≠Φ.


(ii)存在u∈∂U,λ∈(0,1),使得u∈λF(u).
引理4[3]令X是一个Banach空间 ,F:[0,1]×X→P(X)是L1-Carathedory集值映射,SF是非空的,令Θ:L1([0,1],X)→C([0,1],X)是一个线性连续映射,则集值映射
Θ∘SF(x):C([0,1]×X)→Pcp,c(C[0,1],X)
是一个闭图算子.
2 主要结论
首先,列出两个假设条件:
(H1)F:[0,1]×R→P(R),对于每个x∈R,F(•,x)可测.
(H2) 存在一个函数l∈L1([0,1],R+),对于几乎处处的t∈[0,1],有
dH(F(t,x),F(t,y))≤l(t)|x-y|,∀x,y∈R,
其中,dH(0,F(t,0))≤l(t),对于几乎处处的t∈[0,1]成立.
定理1假设(H1)-(H2)成立,若存在一个正数M>0,使得
(4)
则问题(3)在[0,1]上至少存在一个解.
证明定义算子T:C([0,1],R)→P(C[0,1],R)如下:
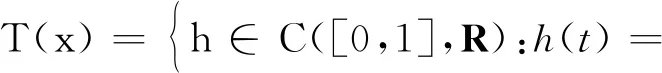
(5)
下面证明,算子T满足引理2的所有条件.将证明分为2个步骤.
步骤1算子T是闭的.令un∈T(x),使得un→u(n→∞).那么u∈(C[0,1],R),存在vn∈SF,x,对于每个t∈[0,1],
由于F具有紧值,假设一个子列vn→v∈L1([0,1],R).因此,有v∈SF,x,对于每个t∈[0,1],可得
un(t)→u=
因此,u∈T(x).这就证明了算子T是闭的.
步骤2T是一个压缩映射.事实上,令x,y∈C([0,1],R),h1∈T(x).存在v1∈F(t,x(t)),使得
由(H2),有
dH(F(t,x),F(t,y))≤l(t)|x-y|,∀x,y∈R.
因此,存在w∈F(t,y),使得
|v1(t)-w(t)|≤l(t)|x(t)-y(t)|,t∈[0,1].
定义U:[0,1]→P(R)如下:
U(t)={w∈R:|v1(t)-w(t)|≤
l(t)|x(t)-y(t)|}.
由于多值算子U(t)∩F(t,y(t))是可测的,存在一个函数v2(t),它是U的可测选择.因此,v2∈F(t,y(t)),对于每个t∈[0,1],有
|v1(t)-v2(t)|≤l(t)|x(t)-y(t)|,
定义
(6)
同理,调换x与y得到
Hd(F(t,y),F(t,x))≤
(7)
综上,证明了算子T是压缩映射,由引理2,至少存在一个不动点,即是问题(3)的一个解.
(H3)F:[0,1]×R→P(R)是Carathedory,并且具有非空紧凸值;
(H4)存在一个连续非减函数ψ:[0,∞)→[0,∞),和一个正的连续函数p,使得
‖F(t,x)‖∶=sup{|v|:v∈F(t,x)}≤
p(t)ψ(‖x‖),(t,x)∈[0,1]×R.
定理2假设(H3)-(H4)成立,若存在一个正数M>0,使得

(8)
则问题(3) 在[0,1]至少存在一个解.
证明此定理的证明基于引理3,即要证明由(2)式定义的算子T满足引理3的所有条件.将定理证明分为四个步骤.
步骤1算子T是将有界集映射为有界集.对正常数r>0,令Br={x∈C([0,1],R):‖x‖≤r}是C([0,1],R)中的有界球,则对于h∈T(x),x∈Br,存在v∈SF,x,使得
类似于(4)式的讨论,有
即
步骤2T映射有界集到等度连续集合.t1,t2∈[0,1],t1 |h(t2)-h(t1)|≤ 不等式右端当t1→t2时趋于0.由Ascoli-Arzela定理,T是全连续算子. 步骤3算子T存在闭图.令xn→x*,hn→T(xn),hn→h.只需证明h*∈T(x*).对于hn∈T(xn),存在vn∈SF,xn,使得下式成立. 要证存在v*∈SF,y,对于t∈[0,1],有 定义一个线性算子Θ:L1([0,1],R)→C([0,1],R)如下: f 注意到 由引理4,Θ∘SF,x存在闭图算子.这就证明了存在某个v*∈SF,x*. 步骤4算子T是凸的.由SF,x的凸性,容易得到结论. 步骤5将证明存在开集U⊂C([0,1],R),对于任意ζ∈(0,1),x∈∂U,x∉T(x). 令ζ∈(0,1),x∈ζT(x),类似于步骤一的讨论,有 由(5)式,存在M使得‖x‖≠M,令 U={x∈C([0,1],R):‖x‖ 考虑如下反周期边值条件的分数阶Langevin微分包含: (9) x→F(t,x)∶= ‖F(t,x)‖∶= sup{|v|:v∈F(t,x)}≤5∶=p(t)ψ(|x|),x∈R, 其中,p(t)=1,ψ(|x|)=5,显然,(H3)-(H4)都满足,令f∈F,则有 存在正实数M,使得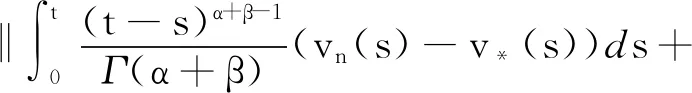


3 例子