分裂四元数的棣莫弗定理
孔祥强
(菏泽学院数学与统计学院,山东 菏泽 274015)
爱尔兰数学家Hamilton于1843年提出了四元数的概念,其形式为H0={a=a0+a1i+a2j+a3k},其中a0,a1,a2,a3∈R,i,j,k满足i2=-1,j2=-1,k2=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j,ijk=-1.James Cockle于1849年研究了分裂四元数,其形式为H={a=a0+a1i+a2j+a3k},其中a0,a1,a2,a3∈R,i,j,k满足i2=-1,j2=1,k2=1,ij=-ji=k,jk=-kj=-i,ki=-ik=j,ijk=1.H为结合且非交换的四维克利福德代数,且含有零因子、幂等元和幂零元[1-3].分裂四元数及分裂四元数矩阵在经典力学和量子力学中均有重要应用[4-5].文献[6]给出了四元数的棣莫弗定理,文献[7]研究了四元数实表示矩阵的棣莫弗定理.文献[8]得到了半四元数的棣莫弗定理,并在文献[9]中给出了半四元数实表示矩阵的棣莫弗定理.Jafari等给出了对偶四元数及其表示矩阵的棣莫弗定理[10-11].文献[12-13]重点研究了分裂半四元数的棣莫弗定理及其应用.文献[14-15]研究了分裂四元数矩阵的实表示及实表示矩阵的特征值和逆矩阵求法.本文研究的对象是分裂四元数,得到两种情形下分裂四元数的棣莫弗定理和欧拉公式;依托所得的棣莫弗定理,给出了分裂四元数方程的求根公式,并讨论了分裂四元数不同方幂之间的联系;最后,探讨了分裂四元数的实表示矩阵的棣莫弗定理.
本文中C表示复数域,R表示实数域,Z表示整数集,Z+表示正整数集,H0表示四元数集.H表示分裂四元数集.
1 分裂四元数
定义1[16]设a=a0+a1i+a2j+a3k,且a0,a1,a2,a3∈R,i2=-1,j2=k2=1,ij=-ji=k,jk=-kj=-i,ki=-ik=j,ijk=1,则称a为分裂四元数,记为a∈H.
设a,b∈H,则a+b=(a0+b0)+(a1+b1)i+(a2+b2)j+(a3+b3)k.若d∈R,则da=(da0)+(da1)i+(da2)j+(da3)k.
a与b的乘积定义为
ab=SaSb-〈Va,Vb〉+SaVb+SbVa+
Va×Vb,
其中〈Va,Vb〉=a1b1-a2b2-a3b3,Va×Vb=(a3b2-a2b3)i+(a3b1-a1b3)j+(a1b2-a2b1)k.a与b的乘积也可记为
性质1设a,b∈H,λ1,λ2∈R,则


4)Nab=NaNb;
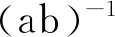
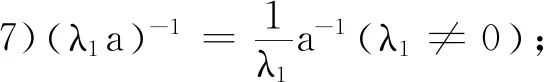
性质2设a,b∈H,且a≠0,若xa=b或ay=b,则

定义2[12]设a,b∈H,a=Sa+Va,b=Sb+Vb,则a与b的内积为
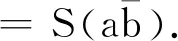
性质3设a,a′,b∈H,则
1)h(ab,a′b)=Nb·h(a,a′);
2)h(ba,ba′)=Nb·h(a,a′);


证明仅给出1)、3)的证明,2)、4)的证明可类似得出.
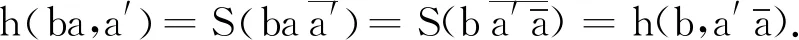
2 分裂四元数的棣莫弗定理


下面分两种情形讨论分裂四元数的棣莫弗定理.



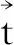


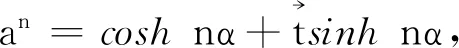

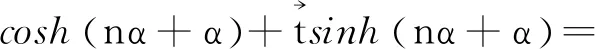
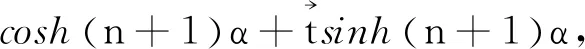
又
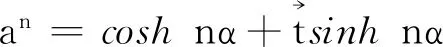



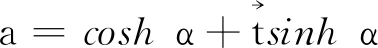
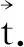



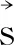
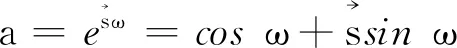

又



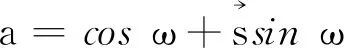
k=0,1,2,…,n-1.
(k=0,1,2,…,n-1)
为方程xn=a的n个根.

(k=0,1,2,3).
故
下面讨论分裂四元数的不同方幂之间存在的联系.
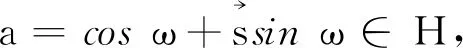
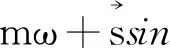
m=n(modq).
由m=n(modq),则m=kq+n(k∈Z),


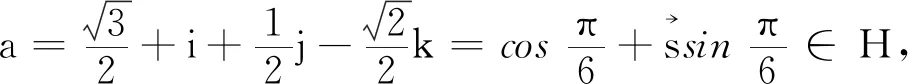
a=a13=a25=a37=…,a2=a14=a26=a38=…,
…… ……
a6=a18=a30=a42=…=-1,a12=a24=a36=a48=…=1,
…… ……
3 分裂四元数的实表示矩阵的棣莫弗定理
3.1 分裂四元数的实表示矩阵
设a=a0+a1i+a2j+a3k∈H,由文献[14-15],任一分裂四元数均与R上的4阶矩阵同构,对分裂四元数的研究可转化为R上4阶矩阵的研究.a的实表示矩阵记为
3.2 分裂四元数实表示矩阵的棣莫弗定理


则
cosω+(s1sinω,s2sinω,s3sinω),
由此,a的实表示矩阵A可改写为

则
由数学归纳法易知定理6成立.

依定理6,可求出A的任意方幂.如
推论1由定理6,对于n≥3,满足An=In的单位分裂四元数的实矩阵A有无穷多个.
4 结语
对分裂四元数理论的研究是四元数量子力学的重要课题.本文研究的重点是将棣莫弗定理推广到分裂四元数及分裂四元数的实表示矩阵上,得到了两种情形下分裂四元数的棣莫弗定理,并给出了分裂四元数的实表示矩阵的棣莫弗定理.根据所得的棣莫弗定理,得到了分裂四元数方程的求根公式,给出了求分裂四元数的任意方幂的方法,并讨论了分裂四元数不同方幂之间的联系.本文的结论,为研究分裂四元数及交换四元数[18]的其他问题提供了理论支撑.以此为基础,还可进一步研究分裂四元数的复表示矩阵的棣莫弗定理等问题.

