有限域上高斯和与一类方程的解数

肖义丽,徐碧云,曹 炜

(宁波大学 数学与统计学院, 浙江 宁波 315211)

(1)

(2)

(3)

定理1设g(x1,…,xn)表示式(3)中的多项式, 且满足gcd(n-1,q-1)=1, 则

1)当p≡3(mod 4)且h为偶数或p≡1(mod 4)时, 有

2)当p≡3(mod 4)且h为奇数时, 有

推论1设g(x1,…,xn)表示式(3)中的多项式, 当n=2时, 则有

1 预备知识

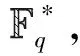
特征的正交性质

引理1[18]对于q=ph, 有

f(x1,…,xn)=a1x1d11…xndn1+…+

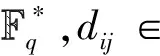
(4)

引理2[9]设n元多项式f如式(4)所示, 则有

(5)

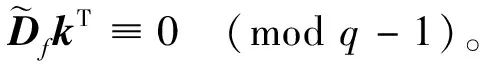
另外，还要用到以下两个组合恒等式(证明略)。

引理3设n≥2为整数, 则有

(6)

2 定理1的证明

证明设g(x1,…,xn)表示式(3)中的多项式, 且有gcd(n-1,q-1)=1。易见，g(x1,…,xn)的增广次数矩阵为(n+1)×(n+1)阶方阵, 即

对g(x1,…,xn)应用引理2。由m=n+1及a1=…=an=1,an+1=-1, 易得

(8)

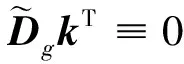
(9)

1)当p≡3(mod 4)且h为偶数，或p≡1(mod 4)时, 由引理1知η(-1)=1,(G2)2j=qj, 故由式(6)与式(9)可得

2)当p≡3(mod 4)且h为奇数时, 由引理1知η(-1)=-1,(G2)2j=(-q)j, 故由式(7)与式(9)可得

证毕。