Hurwitz zeta函数与Kloosterman和及广义Cochrane和的混合均值

张 露，韩 迪

(西北大学 数学学院, 陕西 西安 710127)

对任意实数α(0<α≤1),和复数s=σ+it,当Res>1时,Hurwitz zeta函数ζ(s,α)定义为

(1)

对给定的α,除s=1这一极点外,此函数是可以解析开拓到全平面的。

2000年，Todd Cochrane介绍了Cochrane和,一个类似Dedekind和的和式,其定义如下:

(2)

Dedekind和定义如下:

(3)

2001年,文献[8]研究了C(h,q)以及Kloosterman和

(4)

之间的关系并得到渐近公式：若q是square-full数,则

(5)

其中,e(y)=e2πiy,φ(q)是Euler函数。

2005年,文献[9]定义了广义Cochrane和，

(6)

其中，

Bn(x)是Bernoulli多项式。并计算了C(h,m,n;q)和K(h,1;q)的混合均值：设q是square-full数,对任意奇数m和n,

(7)

2007年,文献[10]得到了渐近公式为:对任意正整数q，有

(8)

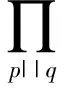
本文研究的混合均值的渐近公式为

其中，C(ab,m,n;q)是广义Cochrane和。

该问题可根据文献[10]的研究成果得出更广泛的结论。利用高斯和的性质以及特征和的估计，将证明以下结论。

定理1对任意正整数q及奇数m和n,有

O(q2+ε)

1 引理

引理1设整数q≥3且(a,q)=1,对任意奇数m和n,有

证明参见文献[9]引理1。

引理2设q和r是2个满足q≥2和(r,q)=1的整数，有

以及

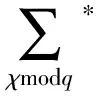
证明参见文献[8]引理3。

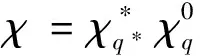
1)若(n,q)>1,则

G(χ,n)=

2)若(n,q)=1,则

证明参见文献[11]引理3。

引理4令q=uv,其中(u,v)=1,u是square-full数或者u=1,v是square-free数。于是有

证明定义δ=ud,γ1=d1g1,γ2=d2g2,因此

(9)

由阿贝尔恒等式可得

(10)

因此

(11)

于是，式(11)可拆分为8个部分,下面将逐一进行计算。

首先计算第1部分。对于(a,q)=1，由引理2有

(12)

可得

(13)

当d1=g1=d2=g2=l=p=k=1,即γ1γ2lpk=d1g1d2g2lpk=1时,得到该条件下式(13)的计算结果,并对其余情形进行估计。因此,可以得到

(14)

式(14)是基于u是square-full数,v是square-free数,并且若u是square-full数, 有恒等式J(u)=φ2(u)/u。

接下来估计第2部分。对任意非主要Dirichlet特征χ1模q和任意z>M,根据它的周期性

(15)

其中，{x}表示x的小数部分。由此可得

(16)

利用与式(16)相同的方法,还可以得到其余6个部分的估计,即

(17)

(18)

(19)

(20)

(21)

(22)

令M=q并结合式(11)至式(22),得到

(23)

引理4证毕。

2 定理1的证明

对任意复数s=σ+it且1/2≤σ<1,由文献[12]可知

(24)

以及

(25)

依据引理1、式(24)和式(25),可得

(26)

(27)

以及

(28)

因此,由引理3和引理4,并结合式(26)至式(28),有

(29)

证毕。