深度教学：指向学生思维深处的路标

王玉英

【摘 要】深度教学是触及知识内核和走进思维深处的教学。针对人教版数学三年级下册第61页“认识面积”中的探究性问题“3×4，2×5两个长方形的面积，孰大孰小”，学生用重叠法比较一次，发现无法解决问题。笔者在课堂上与学生进行深度讨论，引发一场用升级版重叠法比较面积大小的“头脑风暴”。结果表明，我们不仅找到了“剪裁+两次重叠”与“画线+两次重叠”两种解决办法，还借助乘法分配律和图形操作关系式揭示了“多次重叠”背后的数学原理，进而从数形结合的角度深化了对面积本质的理解，促使学生思维走向深处。

【关键词】面积 重叠法 数学原理 质疑 深度教学

一、深度教学之课前慎思

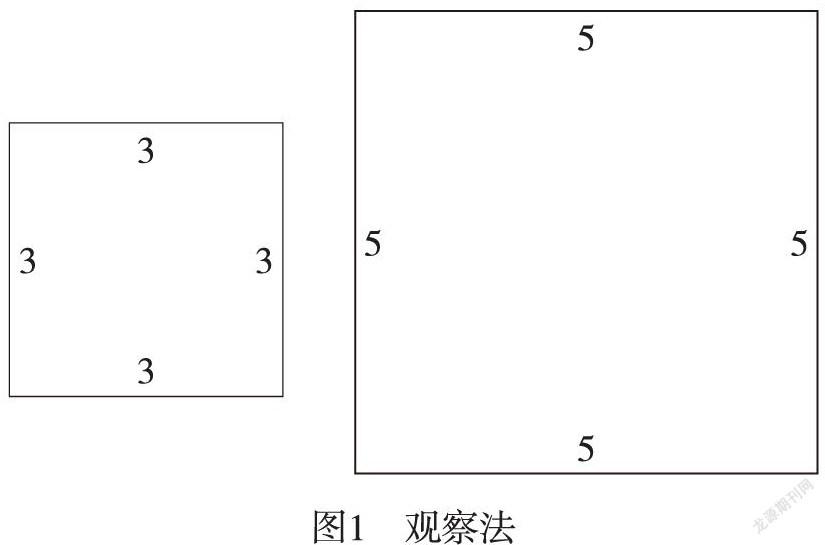
好问题是开启深度教学之门的钥匙，也是激发学生深刻思维的催化剂。在“认识面积”教学中，教材让学生探究3×4和2×5两个长方形的面积大小。一名学生用眼睛观察后，说：“看不出哪个面积大。”另一名学生用重叠法比较一次，然后说：“用重叠的方法也比较不出来，怎么办呢？”教材发问的目的是引出数方格法，但是重叠法真的无效吗？学生用重叠法比较一次，发现无法解决问题。那么，用重叠法比较多次，能解决吗？这引起了笔者的深思，进而提出系列化环环相扣、引人深思的好问题。

（1）什么是重叠法？用重叠法比较面积大小体现了面积的哪个特征？什么样的图形用重叠法比较一次，就能比较出面积大小？

（2）用重叠法比较一次，不能解决的，比较多次，能解决吗？若能，需要比较几次？是有限次吗？

（3）如何设计深度有效的活动，多次重叠就能解决问题？该活动破坏图形的完整性吗？若破坏，又该如何改进？（如长方形钢板，不能破坏其完整性）

（4）“多次重叠”背后的数学原理是什么？又蕴含着什么数学思想？这些原理和思想能被小学生理解和领悟吗？

（5）对于更一般的两个长方形，有限次重叠，能否比较出它们的面积大小？在理论上能否给出相应的证明？能否设计出一个高效的算法，编程后让计算机解决该问题？为解决上述问题，笔者和学生在课堂上动手又动脑，带来了一场别样的、富有深度的精彩盛宴。

二、深度学习之精彩回放

学生真正的“深度学习”是指在教师的引领下，学生围绕挑战性的问题，全身心积极参与、体验成功、获得发展的学习过程。在课堂上，师生借助“头脑风暴”让问题得以解决、原理得以清晰、知识得以内化，把思维引向深处。

【片段1】

通过观察法比较，让学生体会“面积大小”，形成面积表示“一块区域大小”的表象。通过一次重叠，让学生理解“面积的可加性”。

师：刚才我们通过看面、摸面、画面活动，对面积有了初步的认识。那么，你能比较这些图形的面积吗？（出示3×3和5×5两张正方形纸片）

生：一看就知道右边的纸片大。

师：右边的纸片大，意味它所占的区域——大。纸片大，也就是它的面积——大。所以，面积表示——

生：一块区域的大小。

师：差别较大的图形，用观察法就能看出面积大小。那这两张纸片呢？（出示3×4和3×5两个长方形纸片）动手试一试吧。

（发给学生纸片，小组合作探究总结）

生：移动纸片，把它们的边对齐，发现右边的纸片大一点。（同步演示）

师：重叠部分纸片，剩余的部分决定它们的大小，对吗？

生：对。

师：这说明，较大的纸片分成了两部分，哪两部分啊？

生：重叠的部分和剩余的部分。

师：这两部分的面积之和与原来纸片的面积相等吗？

生：相等。

师：这是从求和的角度表述的。如果换成做差的角度，又该怎么表述呢？

生：原来纸片的面积减去重叠部分的面积就是剩余部分的面積。

师：你发现这两张纸片的边有什么特点？

生：有一对边能完全重合，说明这对边长相等。

【片段2】

针对用一次重叠无效的情形，创造性提出“剪裁+多次重叠”与“画线+多次重叠”的两种解决办法，引发一场比较面积大小的“头脑风暴”活动。

师：有相等边长的长方形，重叠法很有效。那么，这两张纸片，用重叠法还能比出大小吗？（出示3×4和2×5两张长方形纸片）

生（满怀信心，边演示边说）：移动纸片，直角边对齐，部分重叠起来，剩余的部分哪个大呢？

（学生陷入困局，百思不得其解时，教师点拨）

师：理论上，要减去重叠部分的面积，那么，在操作中，你怎样做呢？给你一把剪刀，手脑并用，尝试一下。

（学生尝试后，恍然大悟）

生：我有办法了，剪掉重合的部分，再看剩余的部分，谁的面积大。

师：剩余的部分，再怎么比较啊？

生：还用重叠法啊。

师：要是还比较不了，怎么办啊？

生：再剪掉重合的部分，再用重叠法比。

师：反复剪掉重合的部分，直到能用重叠法比较为止。（见图4）用这种方法再试试吧！

师：你们用了几次重叠法？

生：两次。

师：这与普通的重叠法（重叠一次）不同。所以，我们找到了一种新方法，老师给它起名为“剪裁+多次重叠法”，你同意吗？

生：同意。

师：这种方法虽然能比较出面积的大小，但是完整的纸片被剪碎了，破坏了纸片的完整性。很多材料，如钢板，不能破坏它的完整性，又该怎么办？

（学生再次陷入困局， 教师再次点拨）

师：你们怎么剪，沿着谁的边缘？

生：重合部分的边缘。

师：可是这个边缘不能破坏啊。

（学生似乎有所明白，教师继续点拨）

师：这个边缘起到什么作用？是将图形分成两部分吗？

生：是的。

师：那不就是“分界线”吗？

生：不破坏“分界线”？那我在钢板画一条线代替“分界线”，不就可以了吗？

师：对啊，反复沿着重叠的边缘画线，直到能用重叠法比较为止。（见图5）给这种方法起个名字，叫——“画线+多次重叠法”。又是一个好方法。

（学生鼓掌）

【片段3】

借助乘法分配律和链式关系图揭示“多次重叠”背后的数学原理，让学生体会“形使数直观，数使形入微”。

师：这两种方法都需要“多次重叠”。那么，“多次重叠”背后涉及什么数学知识，你知道它的数学原理吗？

原理探究，步骤如下：

① 给出长方形的符号记法。如2×5长方形纸片，记为或 。

② 标出纸片的边长。

③ 两纸片第一次重叠，得图4（上）。

④ 利用片段1中“原面积、重叠面积、剩余面积的关系”，第一次重叠对应的图形操作关系式为

其中，“+”表示图形合并，“=”表示图形拆分或组合。

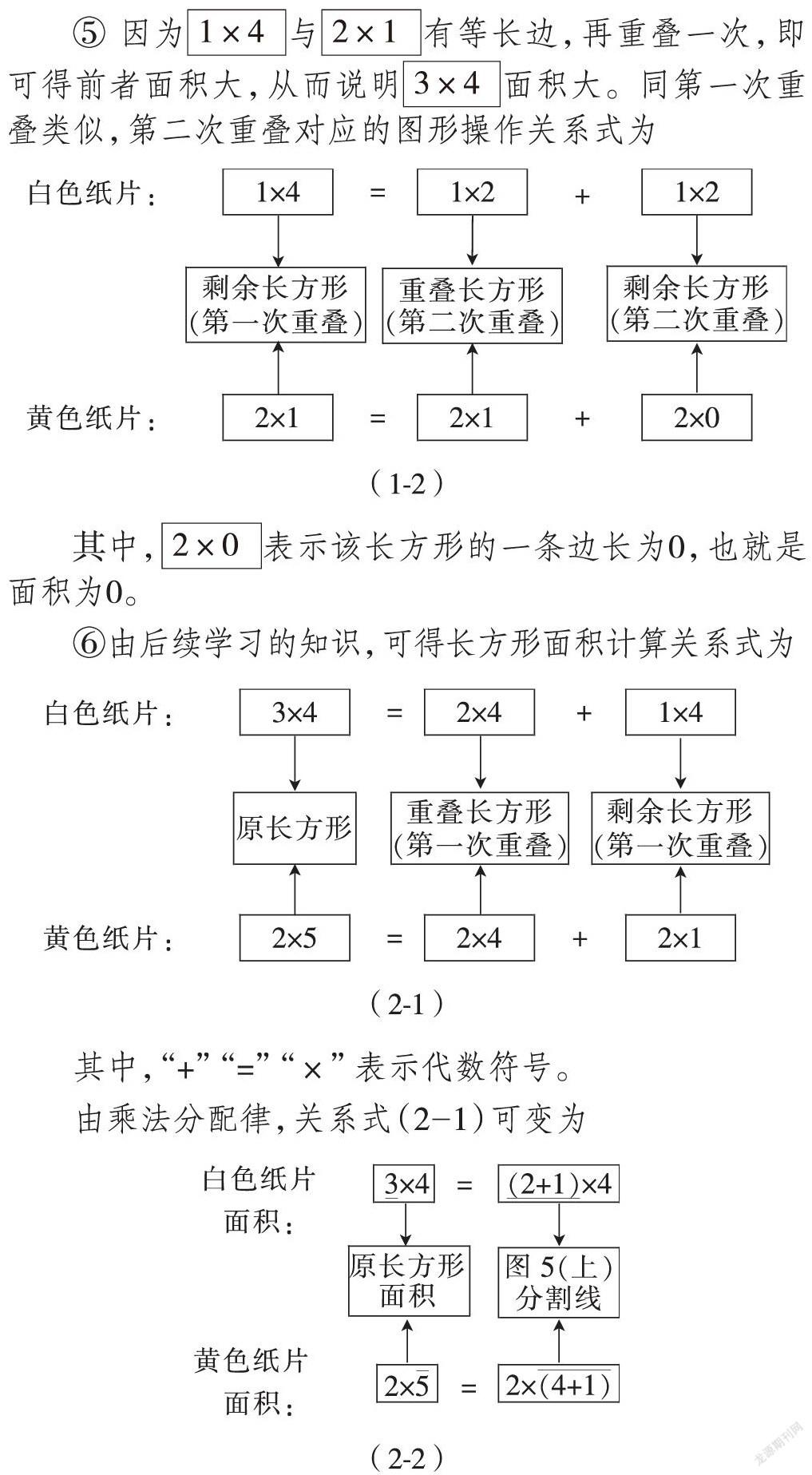
⑤ 因为与有等长边，再重叠一次，即可得前者面积大，从而说明面积大。同第一次重叠类似，第二次重叠对应的图形操作关系式为

其中，表示该长方形的一条边长为0，也就是面积为0。

⑥由后续学习的知识，可得长方形面积计算关系式为

其中，“+”“=”“×”表示代数符号。

由乘法分配律，关系式（2-1）可变为

其中，中 “+”除表示两数字相加外，还可表示原来的边被截成两段，见图5（上）。

⑦ 操作关系式（1-1）和（1-2）是分步的。合并后，用链式表示为

其中，“”指向剩余的长方形。 链式关系式更能直观、清晰地描述图形的分割操作，便于判断原图形面积的大小。

师：一般来说，每次重叠都会有两种情形，它们对应的重叠图形也不同。针对另一种情形，你能一边操作图形，一边写出它的链式关系式吗？

三、师生成长之课后深思

新课程赋予教师新的内涵和新的要求。教师不再是传统的“传道、授业、解惑”者，更不是用现成设计的教案去完成知识传授目标的传递者。进入新世纪，教师理应成为教育教学工作的探索者、研究者。课后深思，则是教师成长的必经之路。

“面积”是平面几何的一个基础概念，而“认识面积”更是整个面积教学的“种子课”。为促进种子的生根、发芽，我们在教学中要深耕细作，不怕花时间。教材上“用重叠的方法也比较不出來”这句话，像是一只亚马孙雨林中的蝴蝶，扇动几下翅膀，就引发了一场用升级版重叠法比较面积大小的“头脑风暴”，形成了现实版的蝴蝶效应：

（1）在课堂上，师生通过手脑并用、思维冲击和思想碰撞，创造性提出比较面积大小的两种方法，即剪裁+多次重叠（破坏图形完整性）和画线+多次重叠（保持图形完整性）。学生亲身经历解决问题的过程，体验问题解决后的欣喜， 以及收获发现新方法的创造感。

（2）师生继续深入探索，揭示了“多次重叠”背后的数学原理，提出了两种图形操作关系式（分步式和链式），进而从数形结合的角度深化了对面积可加性的认识。简单的一句话“重叠法真的无效吗”，竟然引发了一节看得见的生长课，收获了意想不到的惊喜！此外，该课沿着观察图形（观察法）—操作图形（重叠法）—提炼原理（操作关系式）的步骤进行，由浅入深，循序渐进地将学生的思维引向深处。有了重叠法教学的深刻，就有了后续生长的简约（数方格法和测量法教学）。

（3）这节课学生不仅收获了知识和方法，还培养了学生善于思考、勇于探索、敢于质疑的科学精神。传统课堂上大都是教师讲学生听，长此以往，学生习惯了接受式教育，缺乏质疑和创造精神。这节课突破了学生机械接受的思维模式，形成一种积极主动、敢于挑战的创造性思维模式。此外，学生在生疑、质疑、解疑等认识活动中，意识到自己不仅是教材的使用者，还能成为教材建设的参与者和创造者。