数学课外知识《集合》教学设计

李凌志

【摘 要】本教学设计在充分学习理解教材内容和编排意图的基础上，根据三年级学生的思维特点和认知水平，从集合知识的生发点出发，创造性地运用教材，巧妙设计了“趣味分类导入新课、模拟情境探究新知、拓展延伸激发思维”等主要教学环节，让学生在不知不觉中经历维恩图的产生过程，学习集合的相关知识，形成自觉运用集合思想解决简单实际问题的良好思维品质。

【关键词】义务教育;小学数学;教学设计;集合

教学内容：人教版《义务教育教科书 数学》三年级上册第九单元P104—105页例1及“做一做”。

教学目标：在具体情境中认识集合，能正确理解维恩图中各部分所表示的含义;能运用集合思想方法解决生活中简单的实际问题;渗透多种方法解决实际问题的意识，培养学生善于观察、勤于思考的良好学习习惯。

教学过程：

一、趣味分类导入新课

在日常生活中，我们经常会遇到分类的情况，比如：将班上的学生分成男生、女生两类;将垃圾分为可回收垃圾、不可回收垃圾等。接下来，我们一起来做一个关于分类的游戏。

互动游戏：将铅笔、衬衣等物品分成“文具”和“衣物”两大类。

师：有時，我们会把这些集合到一起的铅笔等物品，用一个圈圈起来，再给他们取上名字“文具”。这样是不是更加清楚？再比如这一类，集合到一起，圈起来，再取个名字“衣物”。是不是更加清楚、明了？

其实，像这种将特定的物体集合到一起，用圈圈起来，在数学里面叫——集合。大家听过吗？今天这节课，我们就要来探讨“集合”这个数学问题。

【设计意图：低年级学生以直观形象思维为主，游戏能很快地集中学生的注意力，通过将铅笔、衬衣等物品分成“文具”和“衣物”两大类这个游戏，帮助学生提取“将一些物体集中到一起作为一个整体来认识”这一原有认知，为集合的学习作好知识上的迁移准备。】

二、模拟情境探究新知

（一）情境模拟一：经历相交集合图的产生过程

师：刚才，我们用集合的方法表示物体的分类，是不是好简单？要不要增加难度？

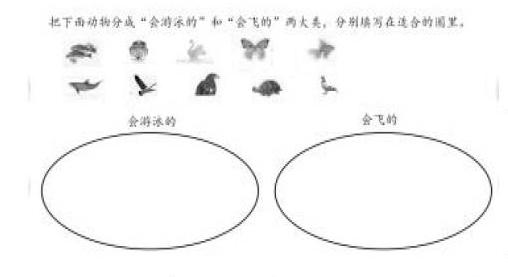
出示情境题二：把下面动物分成“会游泳的”和“会飞的”两大类，分别填写在适合的圈里。（课本P105“做一做”第1题）

学生在试练中进行不下去。师生共同探讨如何解决遇到的新问题。

生：动物更多，有些既会游泳又会飞，如天鹅、大雁不知放在哪个集合圈中，两个集合圈分不了。

教师引导学生思考：天鹅、大雁既会游泳又会飞，那么它们应该既在会游泳的集合圈中，又在会飞的集合圈中。如何做到这一点？

教师提示：我们可否想办法移动这两个集合圈的位置，使天鹅、大雁既在会游泳的集合圈中，又在会飞的集合圈中。

接着，教师拖动集合圈，学生豁然开朗。师生共同完成集合圈中动物的分类。

教师小结：刚才我们把两个集合圈重叠一部分，很好地解决了既会游泳又会飞的动物分类。像这种两个集合圈重叠一部分的情况，在数学里面叫做两个集合“相交”。前面“文具与衣物”“三角形与四边形”都是两个集合完全分开，没有重叠的部分，在数学里面叫做两个集合“不相交”。

【设计意图：创造性地运用“做一做”第1题“动物分类”这一情境素材，让学生继续用集合的方法表示动物的分类，并产生冲突，通过“分不下去、移动集合圈、解决问题”，从中经历维恩图的产生过程，理解两个集合相交的原理和意义。这样设计达到了事半功倍的效果，使得重点内容有了良好开端，难点内容得到初步化解。】

（二）情境模拟二：用集合相交原理解决简单的重叠问题

出示情境题三：课本P104例1。（先不出示问题）

师：从题目中，你了解到了哪些数学信息？

生1：有2项比赛项目，分别是跳绳比赛、踢毽比赛;

生2：参加跳绳比赛的有9人、参加踢毽比赛的有8人;

生3：有些同学两项比赛都参加了，如杨明、刘红、李芳。

师：不错，同学们看得很认真、很仔细。今天我们学习了集合，大家可不可以用集合图来表示这些信息呢？

生：可以。

师：用相交的集合图，还是用不相交的集合图？为什么？

生：用相交的集合图。因为有些同学既参加了跳绳比赛，又参加了踢毽比赛。

学生试着练习，教师点评，重点讲解相交部分表示的是两项都参加的同学。

师：这个集合图是不是表示了上面表格中的所有信息？与表格相比，它还有哪些优点？

生：不但表示出了表格中的所有信息，而且很容易看出有哪些同学两项都参加了，这是它的主要特点。

师：根据这个集合图，你能解答“参加这两项比赛的共有多少人”这个问题吗？（表格下面出示问题）

生1：9+8-3=14（人）。因为参加跳绳比赛的有9人，参加踢毽比赛的有8人，一共是17人，但是有“3人”是两项都参加的，重复计算了1次，所以还要减3。

生2：3+6+5=14（人）。因为“3人”是两项都参加的，还有“6人”是只参加了跳绳比赛的，“5人”是只参加了踢毽比赛的，全部相加一共是14人。

生3：9+5=14（人）。因为参加跳绳比赛的有9人，参加踢毽比赛的8人中有3人包括在这9人中，所以只要再加5人就是全部的人数。

生4：8+6=14（人）。因为参加踢毽比赛的有8人，参加跳绳比赛的9人中有3人包括在这8人中，所以只要再加6人就是全部的人数。

教师点评：在这道例题中，我们用相交的两个集合图表示参加跳绳比赛、踢毽比赛的同学，很清楚地看出有3名同学两项都参加了，通过观察，很容易计算出参加这两项比赛的共有多少人。

【设计意图：在学生初步理解集合相交原理之后，设计“分析表格中的数学信息、用相交集合图表示表格中的数学信息、对照集合图用不同列式解答重叠问题”三个步骤，过渡自然，有利于学生通过具体情境进一步理解集合相交的原理和意义，训练了学生借助直观图，运用集合的思想方法解决简单重叠问题的基本能力。】

三、拓展延伸激发思维

出示情境题：为丰富校园生活，学校定于“六一”儿童节上午举行书法比赛，下午举行绘画比赛。要求每班选5名同学参加书法比赛，3名同学参加绘画比赛。每个班一共要选多少人参加这两项比赛？

師：这是一道生活中的实际问题，谁能快速解答？

生1：5+3=8（人）每个班一共要选8名同学参加这两项比赛。

师：还有其他答案吗？（学生思考）实际上我们在选人参加比赛的时候，首先考虑的是什么？

生：每项比赛都应该派最好的同学去，这样才有可能取得好成绩。

师：对。如果有一个学生书法在班上是第一名，绘画也是班上最好的，那是不是两项比赛都要选他去？这样还需要选8名同学吗？

学生思维活跃，情绪高涨，纷纷列出可能出现的情况。

师：非常好，大家很聪明，把4种可能的情况都估计到了。老师这里用集合图分别表示这些情况，大家看得懂吗？

【设计意图：这是一道开放性的逆向思维题，通过一个常见的事例，将两个集合不相交、相交、包含几种情形列举出来，学生乐于接受，容易理解，题目具有一定的综合性、趣味性和挑战性。通过本题，考查了学生综合运用所学知识，灵活解决实际问题的能力，同时也开阔了学生的数学视野，激发了学生的数学兴趣，为今后集合知识的进一步学习打下了良好基础。】

四、课堂回顾总结提升

师：今天这节课大家有什么收获？

学生自由作答。

五、结束语

本节课的设计，两大理念贯穿其中：一是注重发挥知识生发点的引领作用和认知冲突点的关键作用。“分类”的思想和方法是集合思想的基础，本课把它确定为集合知识的生发点，新课导入、概念内化、新知探究均由它引领展开，课中制造了“具有两种属性的物品在分类时分不下去”的认知冲突，为学生理解集合相交的原理和意义起到了决定性和关键性作用。二是注重模拟情境和互动项目的设计。课中设计了4个情境与互动，贯穿各个环节，涉及的都是学生生活与学习中常见的事例，不仅提高了学生的学习兴趣，激发了学生的好奇心，而且还让学生体会到数学知识与生活的密切联系，让学生在不知不觉中经历集合知识的探究过程，在解决问题的过程中理解集合思想，同时获得了有价值的数学活动经验。

【参考文献】

[1]卢江，杨刚主编.义务教育教科书教师教学用书，数学（三年级·上）[M].人民教育出版社