三余弦公式在求解空间角问题中的应用
◇ 浙江 沈新权(正高级教师)
异面直线所成的角、斜线与平面所成的角以及二面角等概念,构成了比较完整的空间角的概念.学习这些概念并掌握这类问题的求解方法对于学生建立空间观念,提高对空间位置关系的认识,发展逻辑推理、直观想象、数学运算等学科核心素养,起着十分重要的作用.由于三余弦公式联系了线线角和线面角,因此利用三余弦公式在处理和解决一些空间角的问题时有着独特的功效.
1 三余弦公式
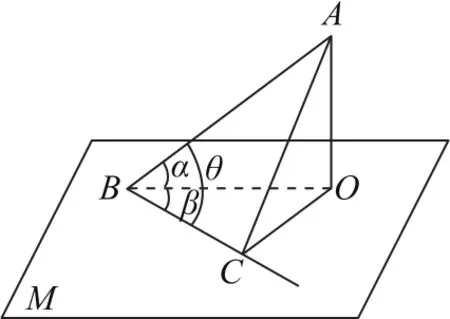
图1
公式如图1所示,若斜线AB与平面M所成角为α,平面M内的一条直线BC与这条斜线AB及AB的射影BO所成的锐角分别为θ,β,则有cosθ=cosα·cosβ(三余弦公式).
证明过点O作OC⊥BC于C,连接AC,则AC⊥BC.在Rt△AOB中在所以有cosθ=cosα·cosβ,结论成立.
说明(1)公式特征:两个互相垂直的平面内(AOB-C)的两条直线(BA与BC)所成角的余弦等于这两条直线与另一个平面所成角(∠OBA与∠OBC,即这两条直线与交线(OB)所成的锐角)的余弦的乘积.
(2)因为θ,α,β均为锐角,且cosθ=cosα·cosβ≤cosα,所以θ≥α,由此可知,一条斜线与已知平面中的任一条直线所成的角中,线面角最小,此即为最小角定理.
2 利用三余弦公式处理和求解空间角
1)比较空间角的大小
例1(2019年浙江卷8,节选)设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点(不含端点),记直线PB与直线AC所成角为α,直线PB与平面ABC 所成角为β,则( ).
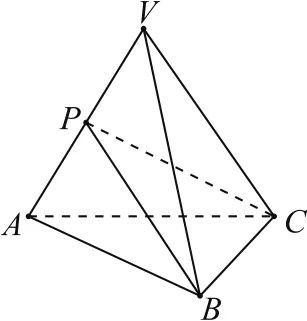
图2
A.α=β B.α>β
C.α<β D.不能确定
分析由于点P是动点,所以直线PB也是动直线,如果直接求α与β的值,再去比较它们的大小,会比较麻烦.但我们注意到β为PB与平面ABC所成的角,而AC在平面ABC内,因此,利用最小角定理即可得到结论.
解由于直线AC在平面ABC内,且PB与平面ABC所成角为β,由最小角定理知α>β,选B.
2)处理线线角
例2如图3,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.求DP与CC′所成角的大小.
分析因为平面BDD′B′与平面ABCD垂直,且它们的交线为BD,所以由∠PDA=60°,∠ADB=45°,利用三余弦公式可求得∠BDP,而DP与CC′所成角与∠BDP互余,问题得以解决.
解设DP与CC′所成的角为θ,因为CC′∥DD′,则 ∠D′DP=θ.因 为 平 面 BDD′B′与 平 面ABCD垂直,由三余弦公式得
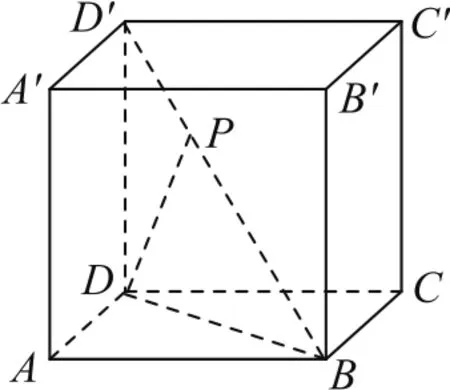
图3
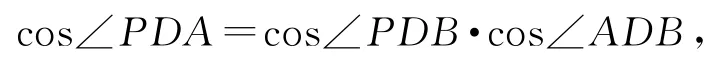
所以
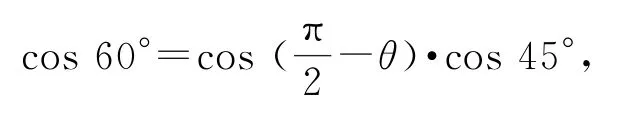
例3(2017年全国卷Ⅲ理16)a,b为空间中两条互相垂直的直线,等腰直角△ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
① 当直线AB与a成60°角时,AB与b成30°角;
② 当直线AB与a成60°角时,AB与b成60°角;
③ 直线AB与a所成角的最小值为45°;
④ 直线AB与a所成角的最小值为60°.
其中正确的是______(填写所有正确结论的编号).
分析这是一个动态的问题,从条件来看,建立空间直角坐标系,然后利用向量法就可以判断结论是否正确.但作为一个填空题,如此“大动干戈”,似乎“小题大做”了.我们先根据题意,画出图形.如图4所示,设CD为直线a,CE为直线b,过B分别作a,b的平行线BM,BN,则直线AB与直线a,b所成的角分别为∠ABM=α,∠ABN=β.注意到,当斜边AB以直线AC为旋转轴旋转时,平面ABC始终与a,b所确定的平面是垂直的,设∠CBM=θ,由题意可知∠CBN=90°-θ.由三余弦公式可以得到α,β与θ的关系,然后进行判断.
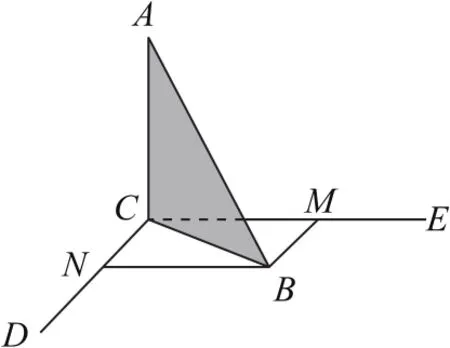
图4
解根据三余弦公式,有cosα=cos∠ABM=同理,有cosβ=由此可以判断命题②③正确.
3)求解线面角
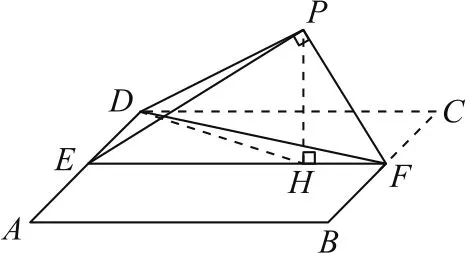
图5
例4(2018年全国卷Ⅰ理18)如图5所示,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.
分析在解决问题(2)时,因为平面PEF⊥平面ABFD,所以过点P作PH⊥EF于H,则PH⊥平面ABFD,因此有平面PDH⊥平面ABFD,连接DH,则有 cos∠PDE=cos∠PDH·cos∠EDH,而∠PDH为DP与平面ABFD所成的角.
解(1)由已知可得,BF⊥PF,BF⊥EF,且PF,EF⊂平面PEF,PE∩EF于E,所以BF⊥平面PEF.又BF⊂平面ABFD,所以平面PEF⊥平面ABFD.
(2)作PH⊥EF,垂足为H,由(1)知,PH⊥平面ABFD,DE⊥PE,不妨设DP=2,则DE=1,从而又PF=1,EF=2,所以PE⊥PF,于是,所以斜线角为∠PDE=60°,因为,设DP与平面ABCD所成角为α,则由三余弦公式知cosα·cos∠EDH=cos60°,从而.
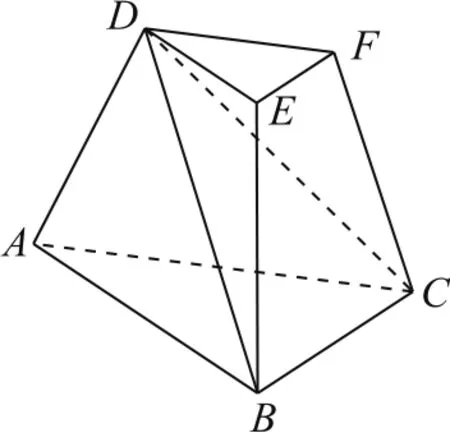
图6
例5(2020年浙江卷19)如图6所示,在三棱台ABC-DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC.
(1)证明:EF⊥DB;
(2)求直线DF与平面DBC所成角的正弦值.
分析(1)因为EF∥BC,所以要证明EF⊥DB,只需证明BC⊥BD.由于平面ACFD⊥平面ABC,且CD,CB分别在平面ACFD与平面ABC内,因此由三余弦公式有cos∠BCD=cos∠ACB·cos∠ACD.
(2)过点D作DO⊥AC于O,因为DF∥OC,所以DF与平面DBC所成角为OC与平面DBC所成角.由∠ACB=∠ACD=45°,得点O在平面DBC上的射影G在∠DCB的角平分线上.在直二面角D-CG-O中,由三余弦公式可得cos∠OCD=cos∠OCG·cos∠DCG,从而可以求出OC与平面DBC所成角即DF与平面DBC所成角的余弦(正弦)值.
解(1)如图7所示,因为平面ACFD⊥平面ABC,所以过D作DO⊥AC于O,连BO,则DO⊥平面ABC.由三余弦公式cos∠BCD=cos∠ACB·cos∠ACD,由∠ACB= ∠ACD=45°,得因为DC=2BC,所以BC⊥BD.因为EF∥BC,所以EF⊥DB.
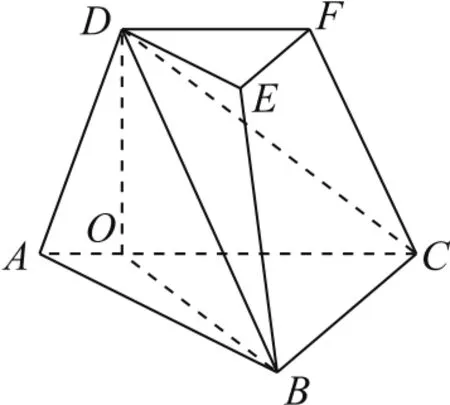
图7
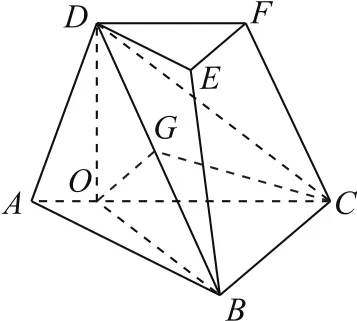
图8
(2)如图8所示,过点D作DO⊥AC 于O,因为∠ACB=∠ACD=45°,所以点O在平面DBC上的射影G一定在∠DCB的平分线上.设直线DF与平面DBC所成角为θ,因为OC∥DF,所以OC与平面DBC所成角也为θ.由(1)知由三余弦定理知cos∠OCD=cosθ·cos∠DCG,即从而sinθ=,即直线DF与平面DBC所成角的正弦值为.
3 判断直线与平面所成角的条数
例6已知二面角α-l-β的大小为50°,P为空间中任意一点,则过点P且与平面α和平面β所成的角都是25°的直线的条数为( ).
A.2 B.3 C.4 D.5
分析过点P作平面α,β的垂线,垂足分别为A,B,则PA,PB所成的角为50°或130°,设过点P且与平面α和平面β所成的角都是25°的直线为m,则m与PA,PB所成的角都为65°.接下来,我们探究m与PA,PB所成的角都为65°的直线条数.
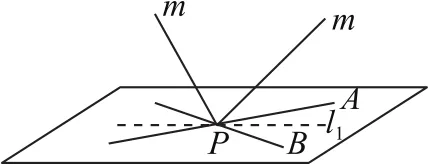
图9
解先假设m与PA,PB所成的角都为θ,则直线m上任意一点在PA,PB所确定的平面上的射影一定在PA,PB的角平分线上.由前面的分析我们知道PA,PB的角平分线l1,l2与PA,PB所成的角分别为25°与65°,设直线m与PA,PB所在平面所成的角为φ,由三余弦公式有cosθ=cos25°·cosφ或cosθ=cos65°·cosφ,由cosθ=cos25°·cosφ≤cos25°,得θ≥25°,即以直线l1为射影的直线m与PA,PB所成的角都为θ的最小值为25°,因此m与PA,PB所成的角都为65°的直线有2条.如图9,由cosθ=cos65°·cosφ≤cos65°,得θ≥65°,此时以直线l2为射影的直线m与PA,PB所成的角都为65°的直线有1条(与PA,PB所成的角为130°的角的角平分线),从而过点P且与平面α和平面β所成的角都是25°的直线的条数为3条.故选B.
4 三余弦公式的推广
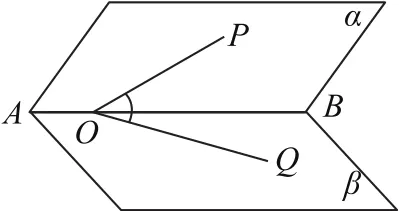
图10
如图10所示,二面角α-AB-β的大小为φ,O为AB上任意一点,OP,OQ分别在平面α,β内,∠POB,∠QOB,∠POQ分别为α,β,θ,则cosθ=cosα·cosβ+sinα·sinβ·cosφ.有的书称此结论为三射线公式.当φ=90°,即二面角α-AB-β为直二面角时的三射线公式就是三余弦公式.利用三射线公式在求解二面角的大小时非常方便,有兴趣的读者可以自行完成三射线公式的证明并探究它的应用.

